⭐Dynamic Programming(동적 계획법)이란?
복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다.
이러한 점이 Divide & Conquer와 동일하지만 다른 점은 '하나의 문제를 단 한 번만 풀도록 한다는 것이다.'
⭐Dynamic Programming(동적 계획법) 설계 절차

⭐최적의 원칙
어떤 문제의 사례에 대한 최적 해가 그 사례를 분할한 부분사례에 대한 최적 해를 항상 포함하고 있으면, 그 문제는 최적의 원칙(The Principle of Optimality)이 적용된다 라고 한다.
하지만 본 문제의 해와 부분 문제의 해가 다르다면 적용되지 않는다. 예를 들어 경로를 구할 때 더 큰 경로를 구하기위하여 부분 경로를 사용할 때 부분 경로와
그 이전에 구해놓은 그 부분 경로와 똑같은 경로를 구했을 때와 다르게 나온다면 적용되지 않는다.
⭐The Binomial Coefficient(이항 계수)
일반적으로 이항 계수를 구하기위해서 수학에서는 의 식을 이용하지만 계산량이 많은 n!이나 k!을 계산하지 않고 다음 식을 사용한다.
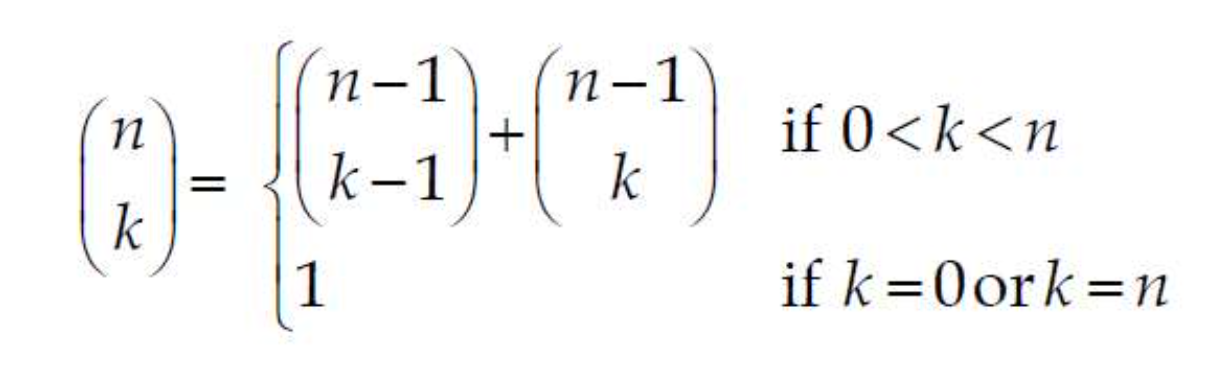
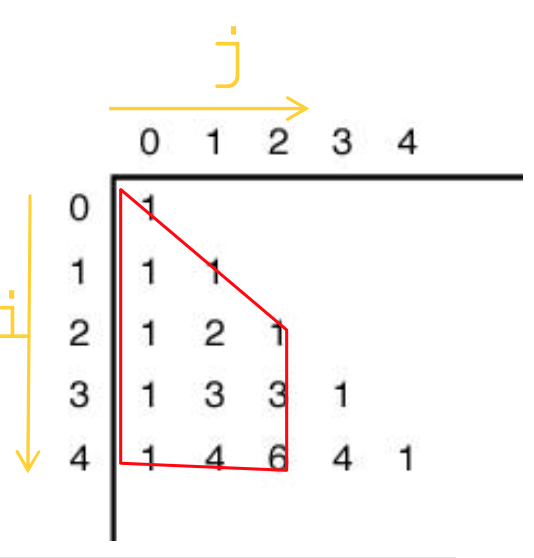
int bin2(int n, int k) {
index i, j;
int B[0..n][0..k];
for(i=0; i<=n; i++)
for(j=0; j <= minimum(i,k); j++)
if (j==0 || j == i) B[i][j] = 1;
else B[i][j] = B[i-1][j-1] + B[i-1][j];
return B[n][k];
}시간 복잡도: (일 때)
⭐Shortest Path(최단 경로) - Floyd's Algo
한 도시에서 다른 도시로 직항로가 없는 경우 가장 빨리 갈 수 있는 항로를 찾는 문제
Optimization Ploblem(최적화 문제)
주어진 문제에 대하여 하나 이상의 많은 해답이 존재할 때,
이 가운데에서 가장 최적인 해답(optimal solution)을 찾아야 하는 문제를 최적화문제(optimization problem)라고 한다.
최단 경로 찾기는 최적화 문제
Floyd's Algo
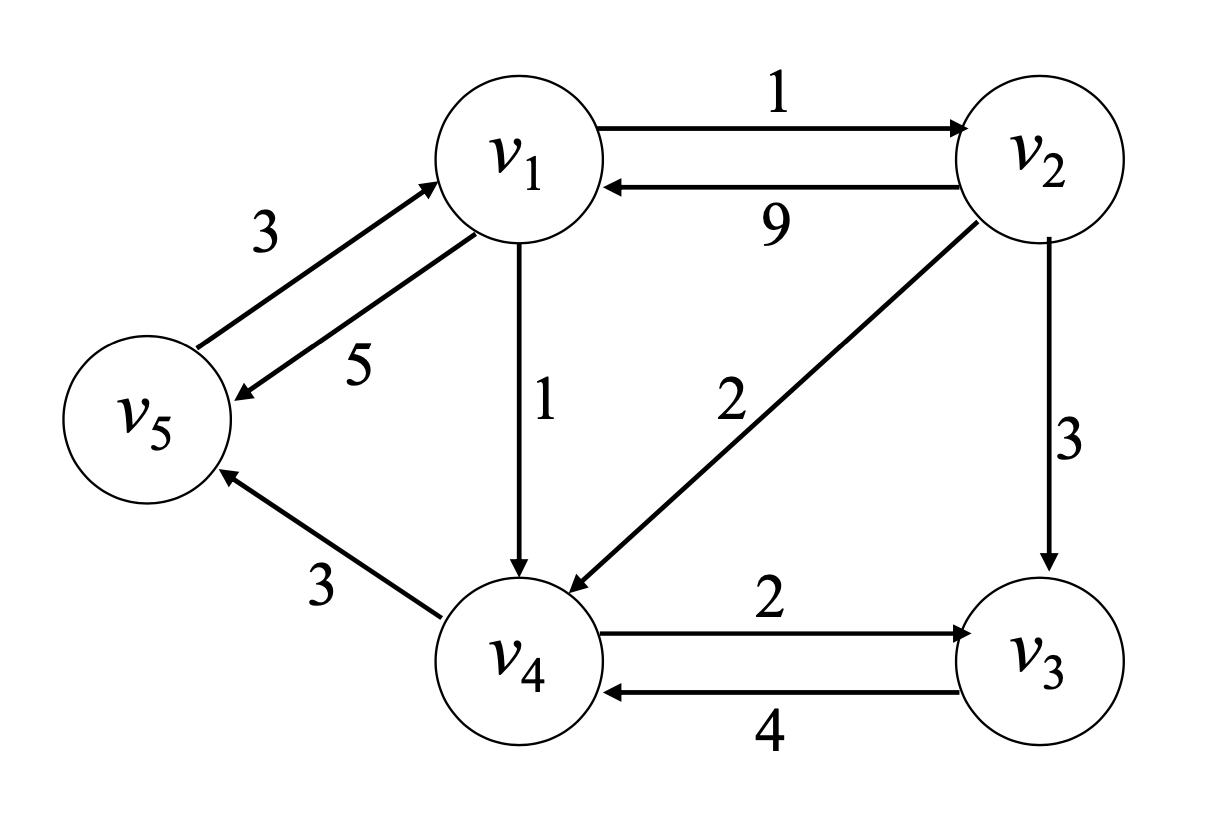

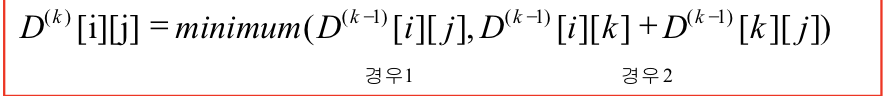
void floyd(int n, const number W[][], number D[][], index P[][]) { index i, j, k;
}
for(i=1; i <= n; i++)
for(j=1; j <= n; j++)
P[i][j] = 0;
D = W;
for(k=1; k<= n; k++)
for(i=1; i <= n; i++)
for(j=1; j<=n; j++)
if (D[i][k] + D[k][j] < D[i][j]) {
P[i][j] = k;
D[i][j] = D[i][k] + D[k][j];
}
} void path(index q,r) {
if (P[q][r] != 0) {
path(q,P[q][r]);
cout << “ v” << P[q][r];
path(P[q][r],r);
} }시간 복잡도:
⭐Chained Matrix Multiplication(연쇄 행렬 곱셈)
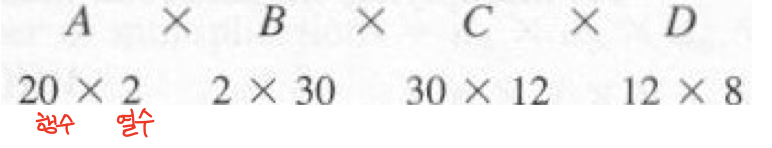
브루트 포스로 풀기 위해서는 의 시간 복잡도를 가지므로 사용할 수 없다. -> DP
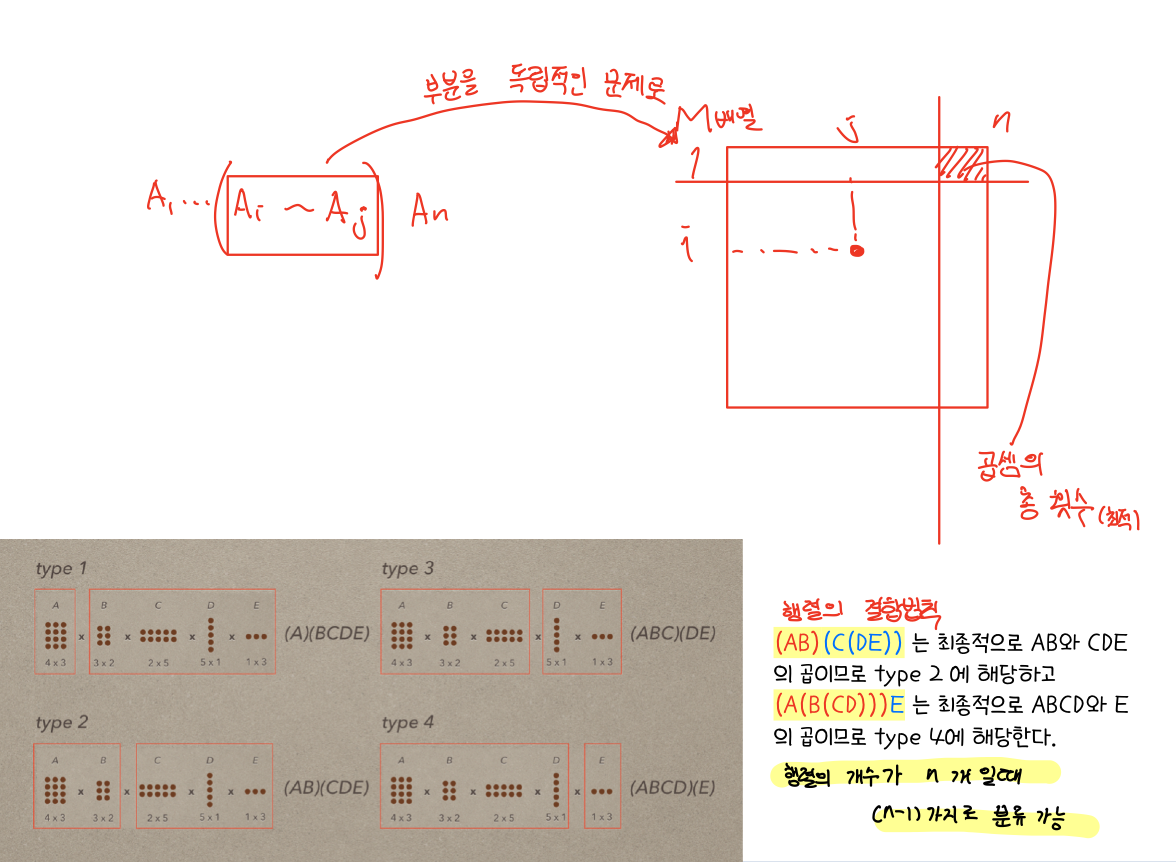


int minmult(int n, const int d[], index P[][]) {
index i, j, k, diagonal;
int M[1..n, 1..n];
for(i=1; i <= n; i++)
M[i][i] = 0;
for(diagonal = 1; diagonal <= n-1; diagonal++)
for(i=1; i <= n-diagonal; i++) {
j = i + diagonal;
M[i][j] = minimum(M[i][k]+M[k+1][j]+d[i-1]*d[k]*d[j]);
//i <= k <= j-1 반복
P[i][j] = 최소치를 주는 k의 값
}
return M[1][n];
}void order(index i, index j)
{
if (i == j)
cout << “A” << i;
else {
k = P[i][j];
}
}시간 복잡도:
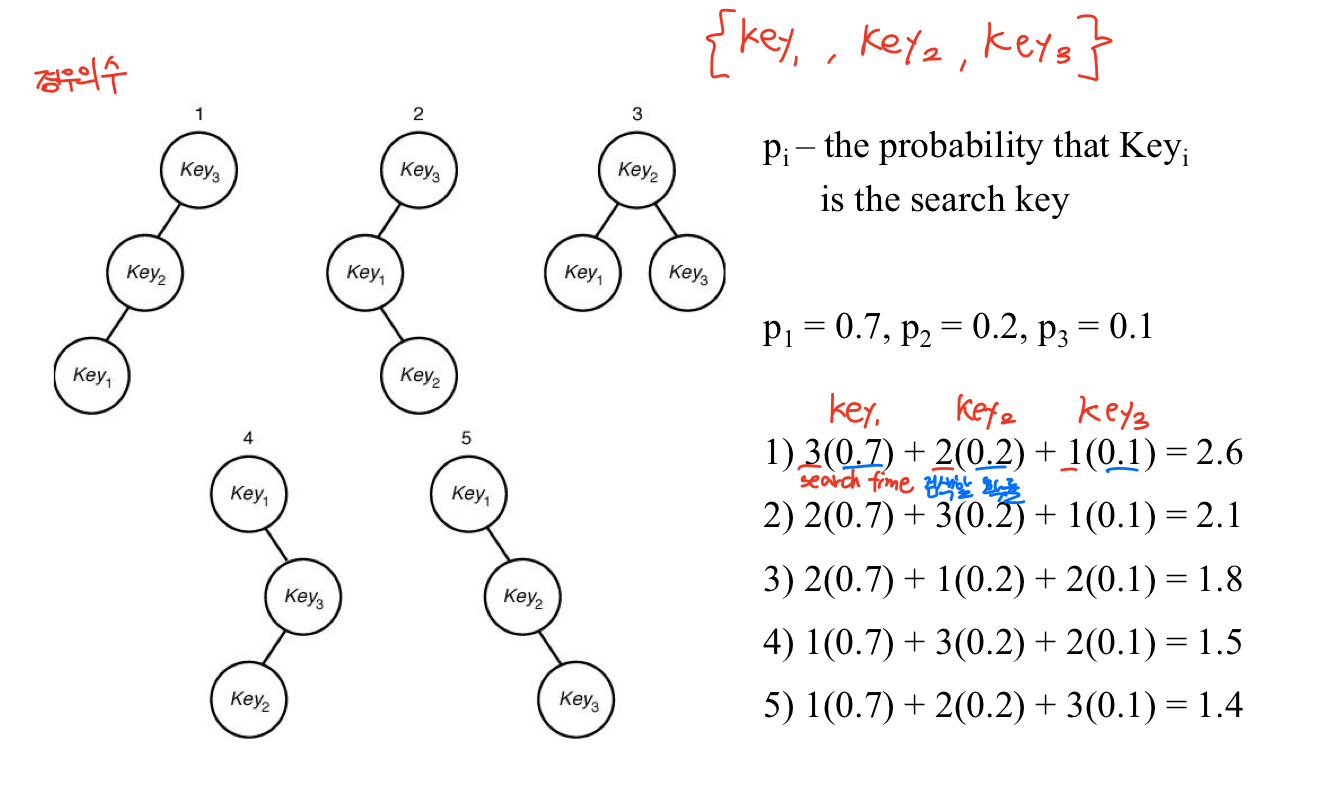
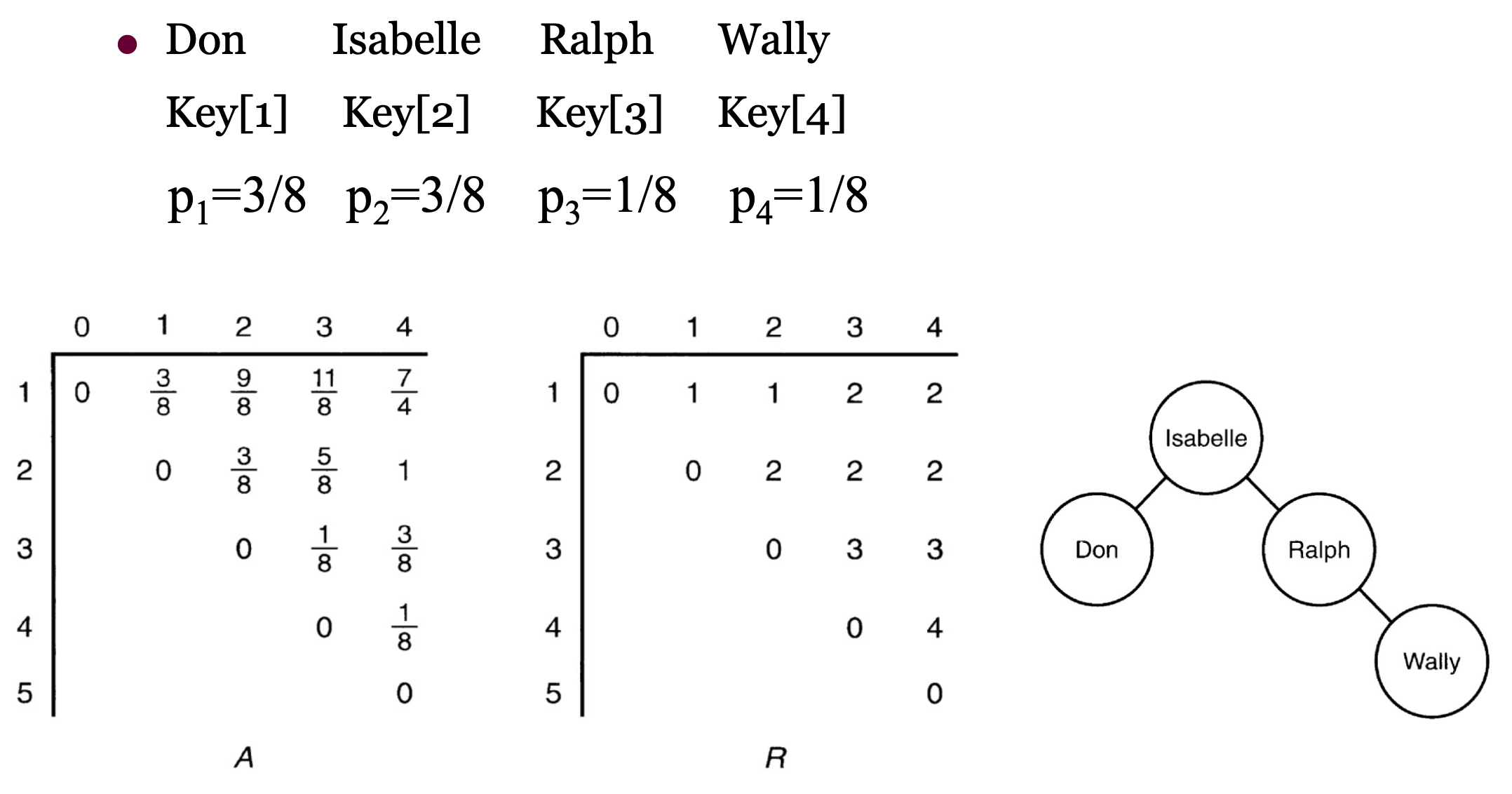
⭐Optimal Binary Search Trees - 최적 이진 탐색 트리
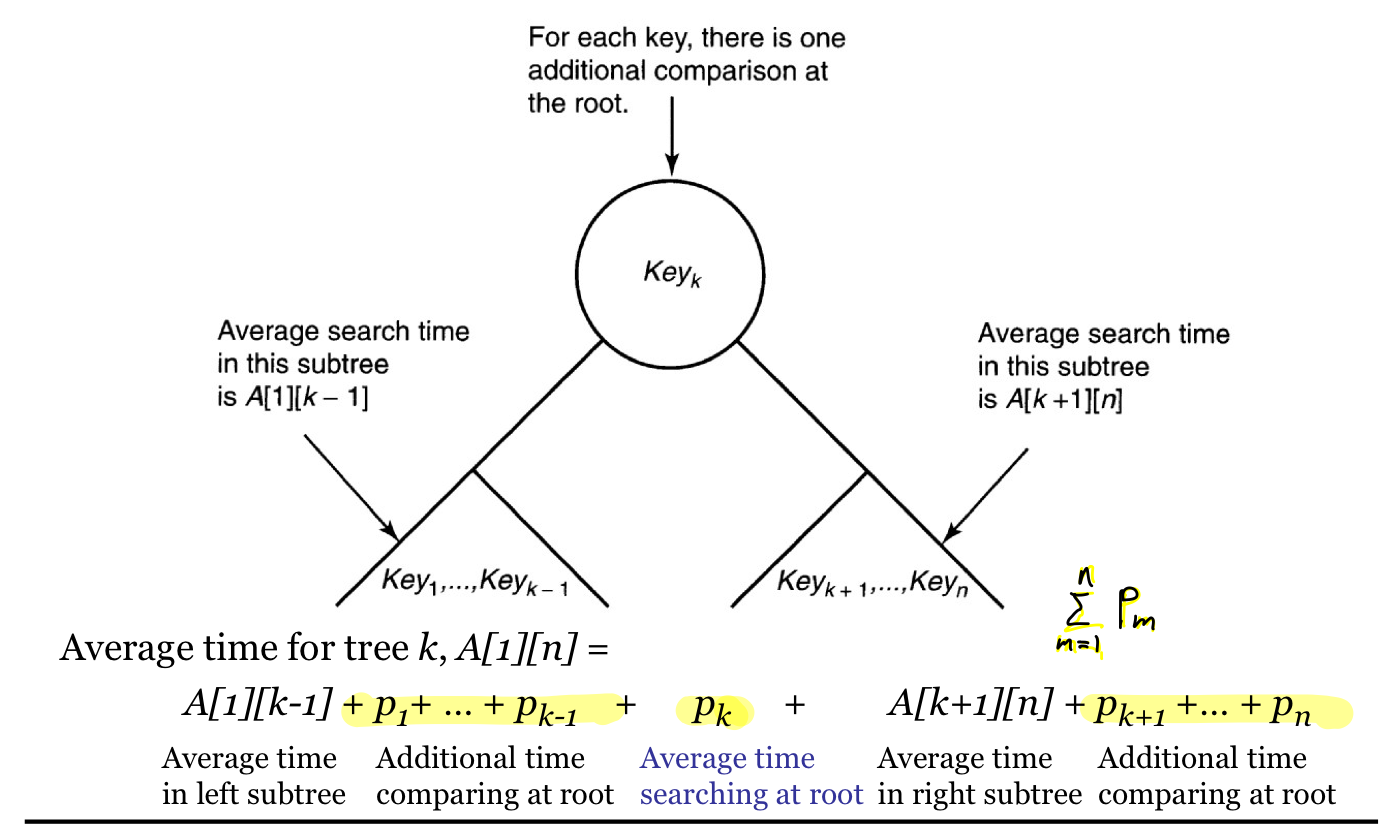
Optimal Binary Search Tree는 각 노드를 찾을 확률을 가질 때 트리 탐색 시 탐색하는 시간이 최적인 트리를 구성하는 알고리즘이다.
키를 찾을 때까지 비교 횟수 - dpth(key) + 1
핵심적인 설계 구조는 루트 노드를 기준으로 이미 구해놓은 트리를 왼쪽과 오른쪽에 붙여서 부분문제로 더 큰 문제를 구해가는 데에 있다.
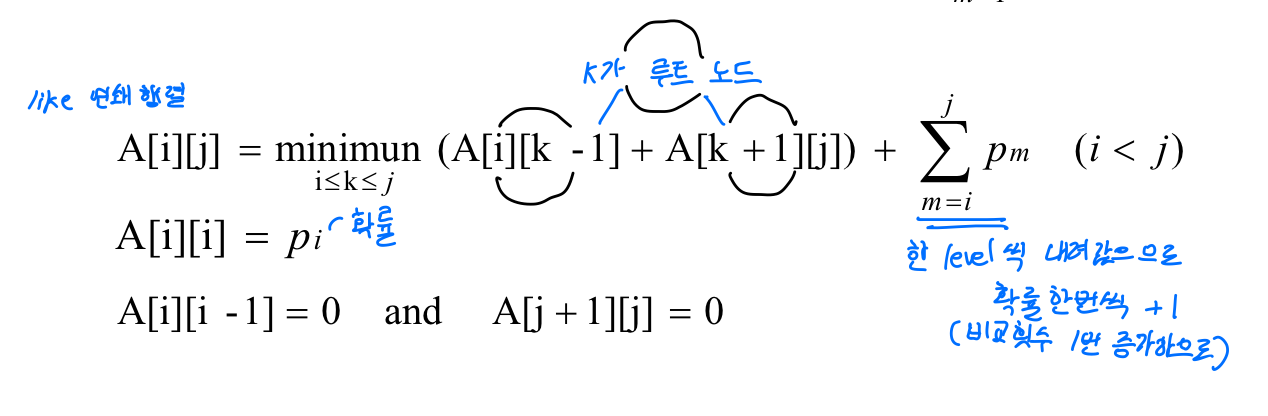
void optsearchtree(int n, const float p[], float& minavg, index R[][]) {
index i, j, k, diagonal;
float A[1..n+1][0..n];
for(i=1; i<=n; i++) {
A[i][i-1] = 0; A[i][i] = p[i]; R[i][i] = i; R[i][i-1] = 0;
}
A[n+1][n] = 0; R[n+1][n] = 0;
for(diagonal=1; diagonal<= n-1; diagonal++)
for(i=1; i <= n-diagonal; i++) {
j = i + diagonal
A[i][j] = min(A[i][k-1]+A[k+1][j]) + p//(p는 i부터 j까지 확률의 합)
//(i<=k<=j)
R[i][j] = a value of k that gave the minimum;
}
minavg = A[1][n];
} nodepointer tree(index i, j) {
index k;
node_pointer p;
k = R[i][j];
if(k==0)
return NULL;
else{
p = new nodetype;
p -> key = key[k];
p -> left = tree(i, k-1);
p -> right = tree(k+1, j);
return p;
}
}
시간 복잡도:
⭐The Traveling SalesPerson Problem - 외판원 문제 - DP 사용 불가
외판원 문제란?
어딘가를 순회하고 다시 돌아오는 알고리즘

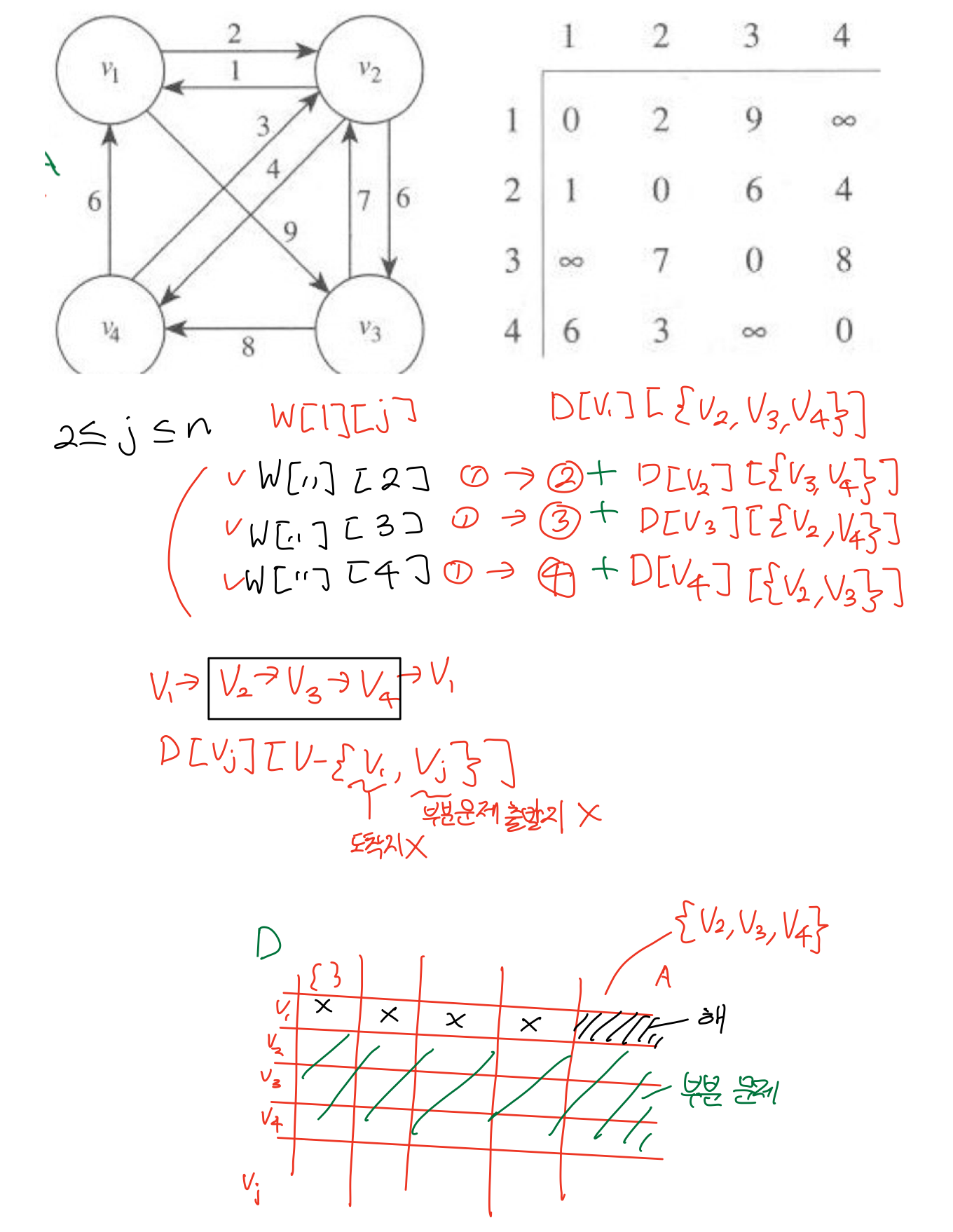

시간 복잡도:
결과적으로 지수승이 나오므로 사용할 수 없다.