
Print Node
순서에 맞게 트리의 노드들을 출력하는 함수를 설계해보자. "순서"를 정의한 다음 Recursive하게 돌면 모든 노드들을 방문하며(Traverse) 출력할 수 있다.
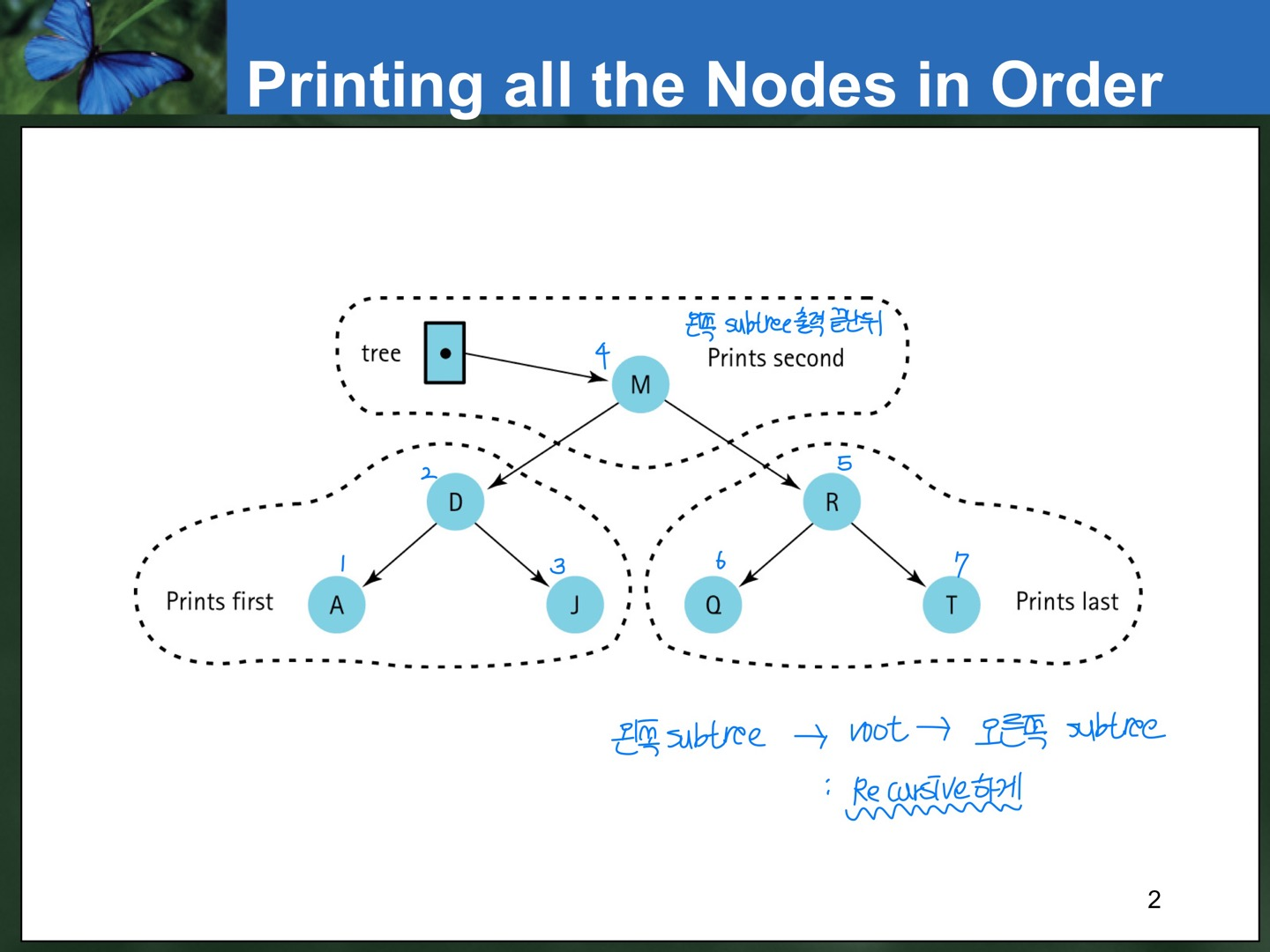
void PrintTree(TreeNode* tree, std::ofstream& outFile)
{
if(tree!=NULL) // general case
{
PrintTree(tree->left, outFile);
outFile<< tree->info;
PrintTree(tree->right, outFile);
}
// base case : tree==NULL일 때 do nothing
}Deconstructor
constructor의 경우에는 "root=NULL"이라고 설정해주면 끝이지만, Deconstructor의 경우에는 주의해야 한다. tree 포인터는 root node만 가리키고 있으므로, "delete tree;"만 실행하면 root node만 지워지고 나머지의 포인터들은 남아 있는 dangling pointer 문제가 발생한다. 따라서 모든 노드를 방문하면서 child->parent 방향으로 일일히 각각 지워줄 필요가 있다.
void Destroy(TreeNode*& tree);
TreeType::~TreeType()
{
Destroy(root);
}
void Destroy(TreeNode*& tree)
{
if(tree!=NULL) //general case
{
Destroy(tree->left);
Destroy(tree->right);
delete tree; // 반드시 왼쪽 오른쪽 다 지우고나서 자신 지워야 한다. 그래야 왼/오가 존재.
}
//base case : tree==NULL 이면 do nothing
}Copy Constructor
linked list와 마찬가지로 tree 포인터만 복사하면 root만 쉐어하게 되는 문제가 발생하므로 전부 독립적으로 만들어줘야 한다. (여기 좀 더 고민해봐야 할 듯)
if (originalTree is NULL)
Set copy to NULL
else
Set Info(copy) to Info(originalTree) // deconstructor와 반대로 왼쪽과 오른쪽이 존재하려면
// 자신이 먼저 복사되어야 한다.
Set Left(copy) to Left(originalTree)
Set Right(copy) to Right(originalTree)코드로 구현하면 다음과 같다.
TreeType::TreeType(const TreeType& originalTree) // reference로 받아서 메모리 할당X, 이름을 share한다.
{
CopyTree(root, originalTree.root);
}
void CopyTree(TreeNode*& copy, const TreeNode* originalTree)
// parent에도 영향가도록 refernece pointer로 받는다.
{
if(originalTree == NULL)
copy=NULL;
else
{
copy=new TreeNode; // 알아서 앞에서 호출한 애로부터 link가 생성된다.
copy->info=originalTree->info;
CopyTree(copy->left, originalTree->left);
CopyTree(copy->right, originalTree->right);
}
}Tree Traversal Methods
- Tree Traversal은 트리에 있는 모든 노드를 방문한다는 것을 의미한다.
- 방문한다는 것은 알고리즘이 노드 안에 있는 값에 무언갈 한다는 것을 의미한다. (예:출력)
✏️ Inorder Traversal : 노드(본인) 중심. 왼->나->오 순서 ( print )
✏️ Postorder Traversal : 내가 제일 뒤. 왼->오->나 순서 ( delete )
✏️ Preorder Traversal : 내가 제일 먼저. 나->왼->오 순서 ( copy )
Inorder
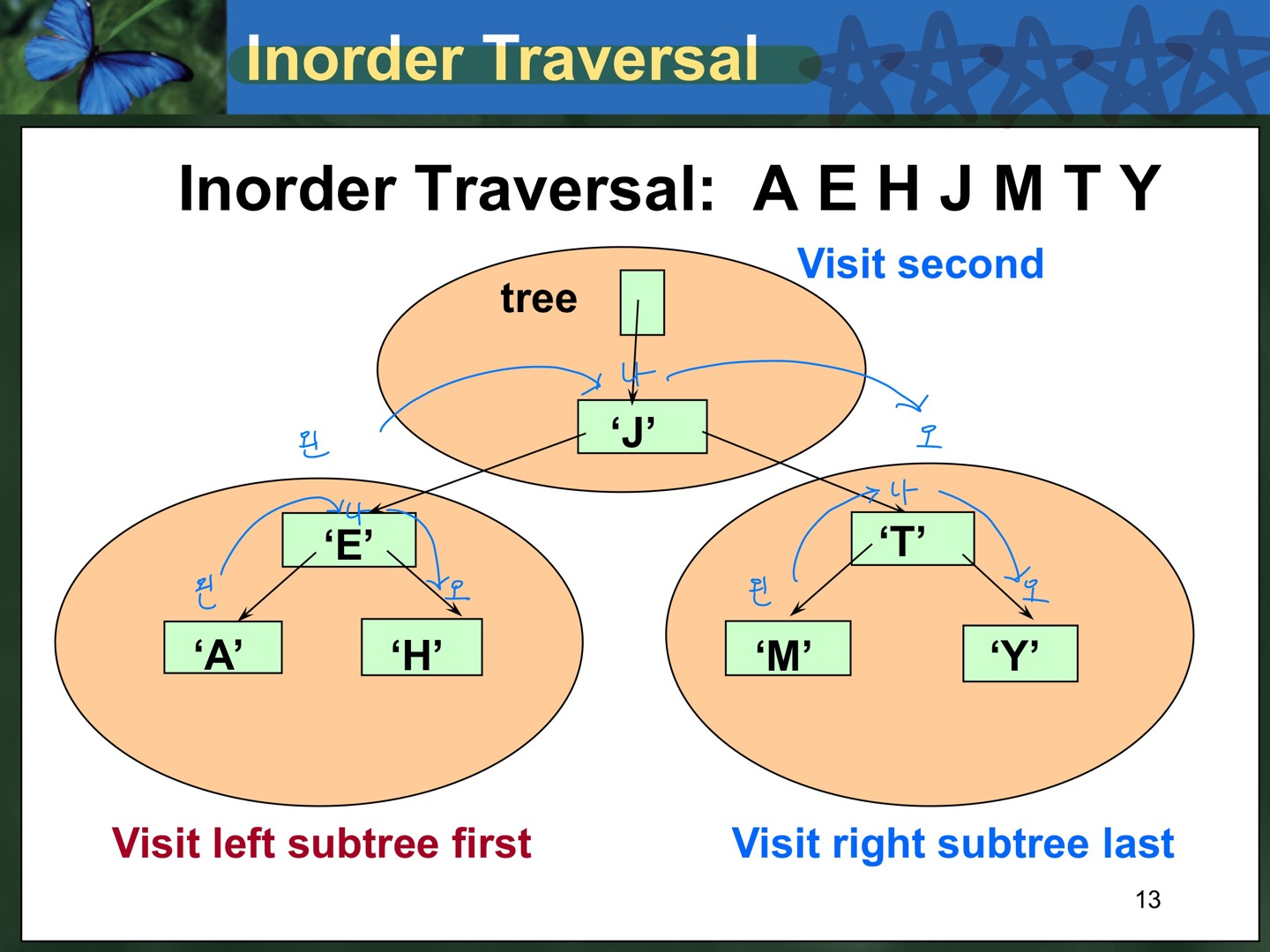
void InOrder(TreeNode* tree, QueType& inQue) // 2차원 tree를 1차원으로 저장하기 위해 queue에 저장
{
if(tree!=NULL) // general case
{
InOrder(tree->left, inQue);
inque.Enqueue(tree->info);
InOrder(tree->right, inQue);
}
// base case : tree == NULL
}Postorder
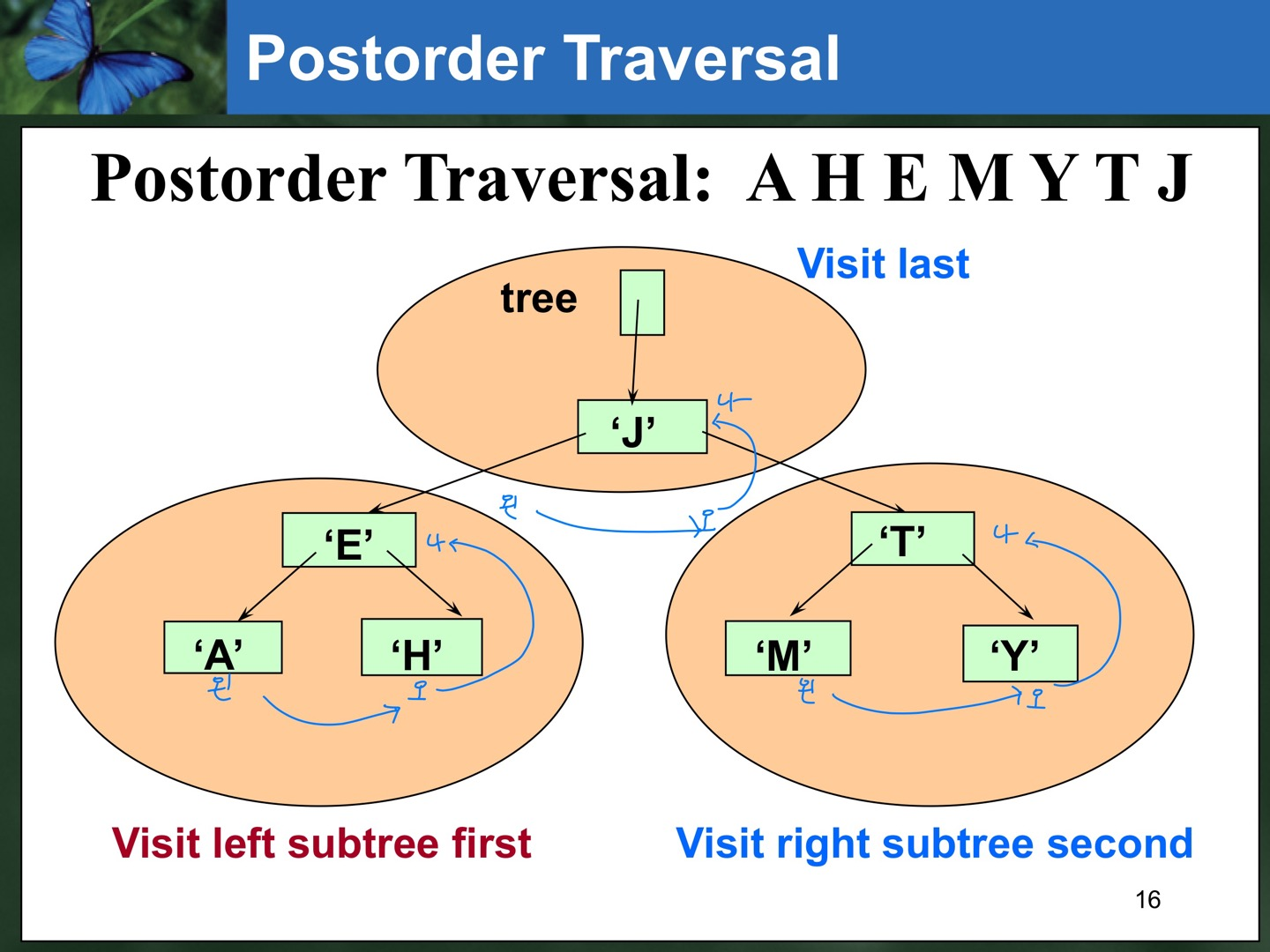
void PostOrder(TreeNode *tree, QueType& postQue)
{
if(tree!=NULL)
{
PostOrder(tree->left, postQue);
PostOrder(tree->right, postQue);
postQue.Enqueue(tree->info);
}
}Preorder
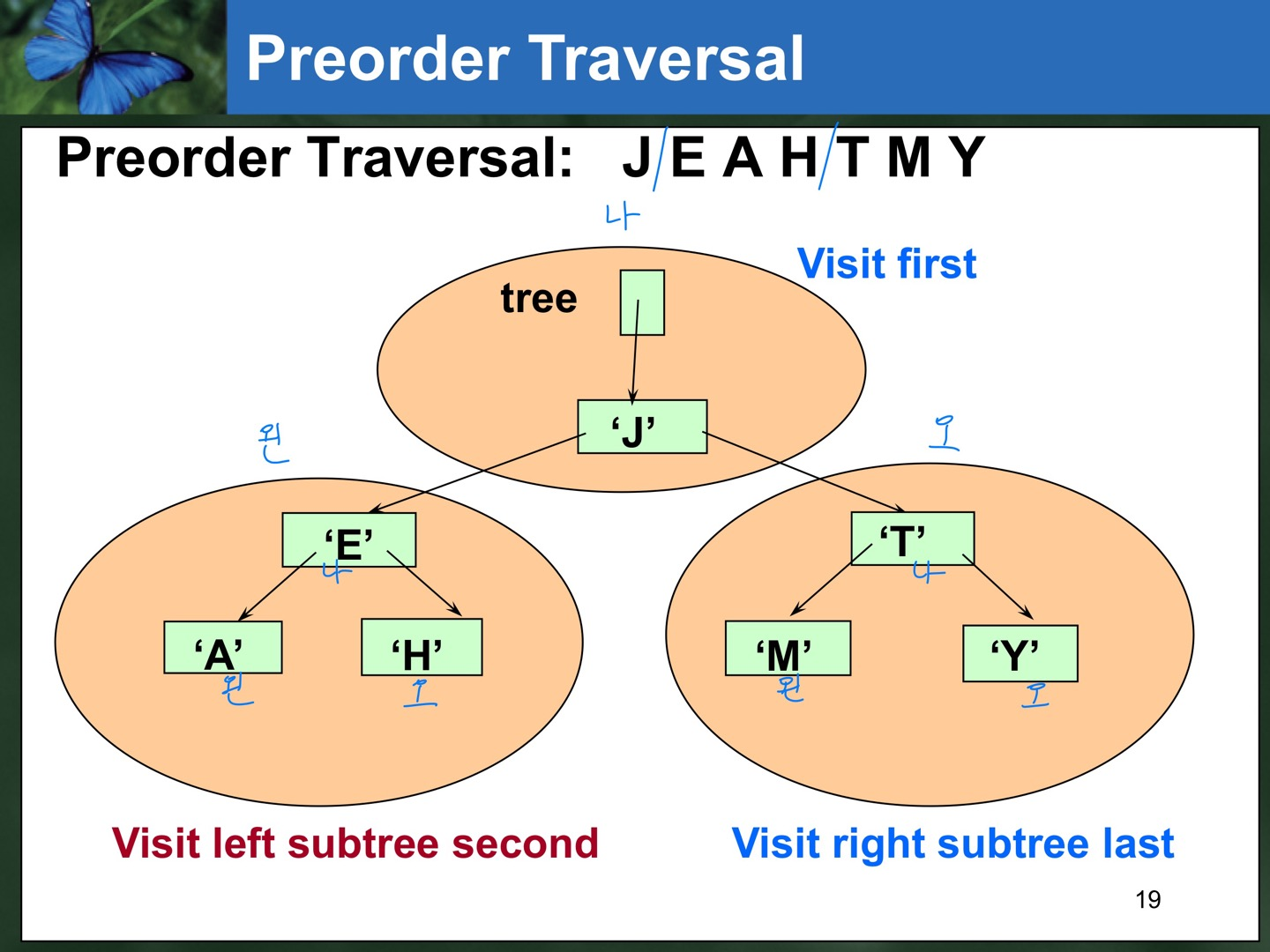
void PreOrder(TreeNode* tree, QueType& preQue)
{
if(tree!=NULL)
{
preQue.Enqueue(tree->info);
preOrder(tree->left, preQue);
preOrder(tree->right, preQue);
}
}ResetTree & GetNextItem
- ResetTree는 가리키는 순서에 따라 노드를 담는 Que를 만든다.
- GetNextItem은 적절한 Que에서 노드의 내용들을 가져온다.
enum OrderType {PRE_ORDER, IN_ORDER, POST_ORDER}; // compiler가 내부적으로 int로 mapping하는 symbol
class TreeType {
public:
// samse as before
prevate:
TreeNode* root;
QueType preQue;
QueType inQue;
QUeType postQue;
};ResetTree
void TreeType::ResetTree(OrderType order)
{
switch(order)
{
case PRE_ORDER : PreOrder(root, preQue);
break;
case IN_ORDER : InOrder(root, inQue);
break;
case POST_ORDER : PostORder(root, postQue);
break;
}
}GentNextItem
void TreeType::GetNextItem(ItemType& item, OrderType order, bool& finished)
// OrderType order : 2차원 to 1차원 mapping 방법
// next를 정의할 수 있게 된다. 다음이 존재하면 전체를 보는 iteration(for문)을 가능하게 한다.
{
finished=false;
switch(order)
{
case PRE_ORDER : preQue.Dequeue(item);
if (preQue.IsEmpty())
finished=true;
break;
case IN_ORDER : inQue.Dequeue(item);
if (inQue.IsEmpty())
finished=true;
break;
case POST_ORDER : postQue.Dequeue(item);
if (postQue.IsEmpty())
finished=true;
break;
}
}Iterative Versions : FindNode
void FindNode(TreeNode* tree, ItemType item, TreeNode*& NodePtr, TreeNode*& parentPtr)
{
nodePtr=tree;
parentPtr=NULL;
bool found=false;
while(nodePtr!=NULL & !found) // 끝에 도달하기 전까지 , 못 찾은 동안
{
if(item<nodePtr->info)
{
parentPtr=nodePtr; // parent를 바꿔줘야 한다. 내가 parent가 된다.
nodePtr=nodePtr->left; // 내 왼쪽을 nodePtr로 설정해준다.
}
else if (item>nodePtr->info)
{
parentPtr=nodePtr;
nodePtr=nodePtr->right;
}
else
found=true;
}
}InsertItem
아이템을 넣는 InsertItem의 메커니즘을 다음과 같이 생각할 수 있다.
- 새 노드를 만들고 값을 채운다.
- 들어갈 위치를 찾고 알맞게 붙여준다.
주의할 점 : 가장 처음 들어갈 때, 즉 parentPtr==NULL일 때 tree를 newNode로 설정해주는 예외 케이스를 명시해줘야 한다.
- &를 안쓰니까 parent node도 저장하고 함수 parameter로 함께 넘겨준다.
void TreeType::InsertItem(ItemType item)
{
TreeNode* newNode;
TreeNode* nodePtr;
TreeNode* parentPtr;
// 새 노드 생성
newNode = new TreeNode;
newNode->info=item;
newNode->left=NULL;
newNode->right=NULL;
// newNode의 위치를 찾아서 연결해준다.
FindNode(root, item, nodePtr, parentPtr);
if(parentPtr==NULL)
root=newNode;
else if(item<parentPtr->info)
parentPtr->left=newNode;
else
parentPtr->right=newNode;
}DeleteItem
void TreeType::DeleteItem(ItemType item)
{
TreeNode* nodePtr; // 지우고자 하는 노드를 pointing 하는 포인터
TreeNode* parentPtr;
FindNode(root, item, nodePtr, parentPtr);
if(nodePtr==root)
DeleteNode(root);
else
{
// nodePtr이 parent의 왼쪽인지 오른쪽인지에 대한 정보는 없기 때문에 case를 나눠야 한다.
if(parentPtr->left == nodePtr)
DeleteNode(parentPtr->left);
else
DeleteNode(parentPtr->right);
}
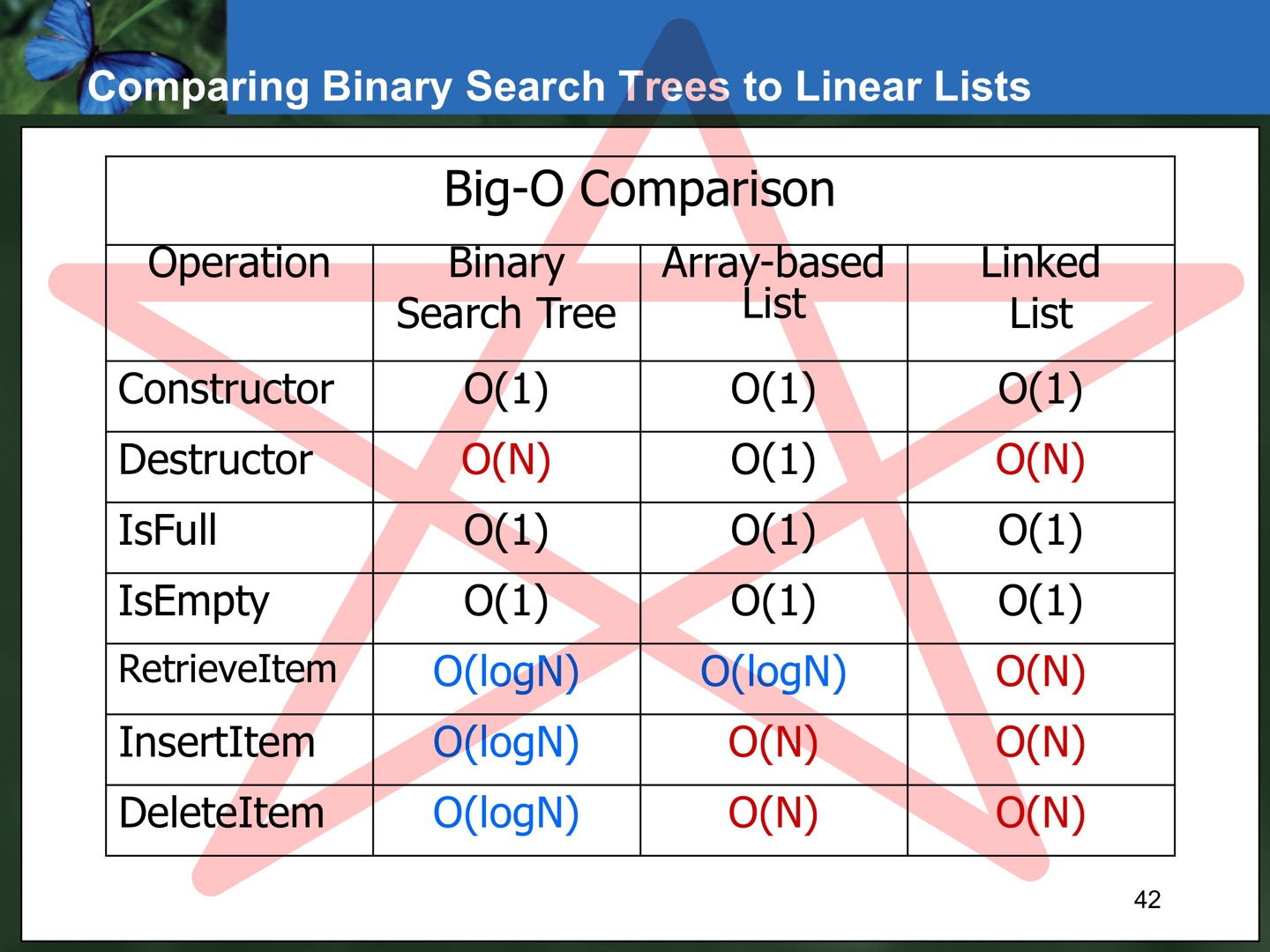
}Time Complexity
Array Representation
포인터 하기 싫으면 array로도 구현할 수 있다. array로 구현하면 node에 대한 규칙이 존재한다.
자기 자신을 index 번째 인덱스에 있다고 하면
- Left Child는 index*2+1 번째 인덱스에 있다.
- Right Child는 index*2+2 번째 인덱스에 있다.
- Parent는 (index-1)/2 번째 인덱스에 있다.
i가 0부터 시작하기 때문에 +1과 +2가 붙는다. 이는 최대 2개만 들어가는 BST라 가능한 구현이다.
Full Binary Tree & Full Complete Tree


