1. numpy
넘파이란?
- Tensors 다차원 배열로 데이터를 표현하는 방법입니다. 스칼라(0차원 텐서), 벡터(1차원 텐서), 행렬(2차원 텐서), 다차원 배열 등이 모두 텐서의 예시
- Tensor Operations(텐서 연산)
- 텐서의 덧셈과 뺄셈: 넘파이에서는
+및-****연산자를 사용하여 텐서 간의 요소별 덧셈과 뺄셈을 수행 - 행렬 곱셈:
np.dot()또는@연산자를 사용하여 두 행렬을 곱 - 스칼라 곱셈: 스칼라 값을 텐서와 곱하는 연산은 각 요소에 스칼라 값을 곱하여 수행
- 텐서의 변환과 크기 변경: 넘파이에서는
reshape()및transpose()와 같은 함수를 사용하여 텐서의 모양을 변경하거나 전치(transpose)를 수행 - 활성화 함수 적용: 시그모이드, 렐루, 소프트맥스 등과 같은 활성화 함수를 텐서에 적용하여 신경망의 출력을 계산
- 텐서의 덧셈과 뺄셈: 넘파이에서는
- Vectorizaion
- Efficiency
- Other Libraries
tensor: 다차원의 배열의 통칭
2. Objects and ndarrays
Objects in python
type() function
a = [1,2,3]
b = {'a':1, 'b':2, 'c':3}
c = (1, 2, 3)
print(type(a))
print(type(b))
print(type(c))
---
<class 'list'>
<class 'dict'>
<class 'tuple'>출력되는 데이터의 클래스를 보면 리스트 / 딕셔너리 / 튜플 이 나오는 것을 알 수 있다.
즉, 데이터 타입 이전에 오브젝트를 알아보는 것이 관건이라고 할 수 있다.
type() Function
#instantiate a list
a = [1,2,3]
#append 메서드를 이용해 리스트 3번째를 만들어준다
a.append(4)
print(a)간단한 예시지만, 오브젝트를 알아봐야 한다.
Object = Data + Methods
오브젝트는 데이터와 메서드가 합쳐진 것이라는 것을 잊어선 안된다.
dir() function
a = [1, 2, 3]
for attr in dir(a):
print(attr)
---
__add__
__class__
__class_getitem__
__contains__
__delattr__ 등등,,,이렇게 많은 메세드가 존재한다. 외울 필요는 없지만 활용할 수 있기는 해야할듯
- a - b = a.sub(b))
- a * b = a.mul(b))
- a**b = a.pow(b))
- a / b = a.truediv(b))
- a // b = a.floordiv(b))
- a % b = a.mod(b))
이렇게 스페셜 메서드를 활용해 연산을 처리할 수 있다.
dir() function
뿐만 아니라 directory에서도 특정 메서드가 존재한다.
a = [1, 2, 3]
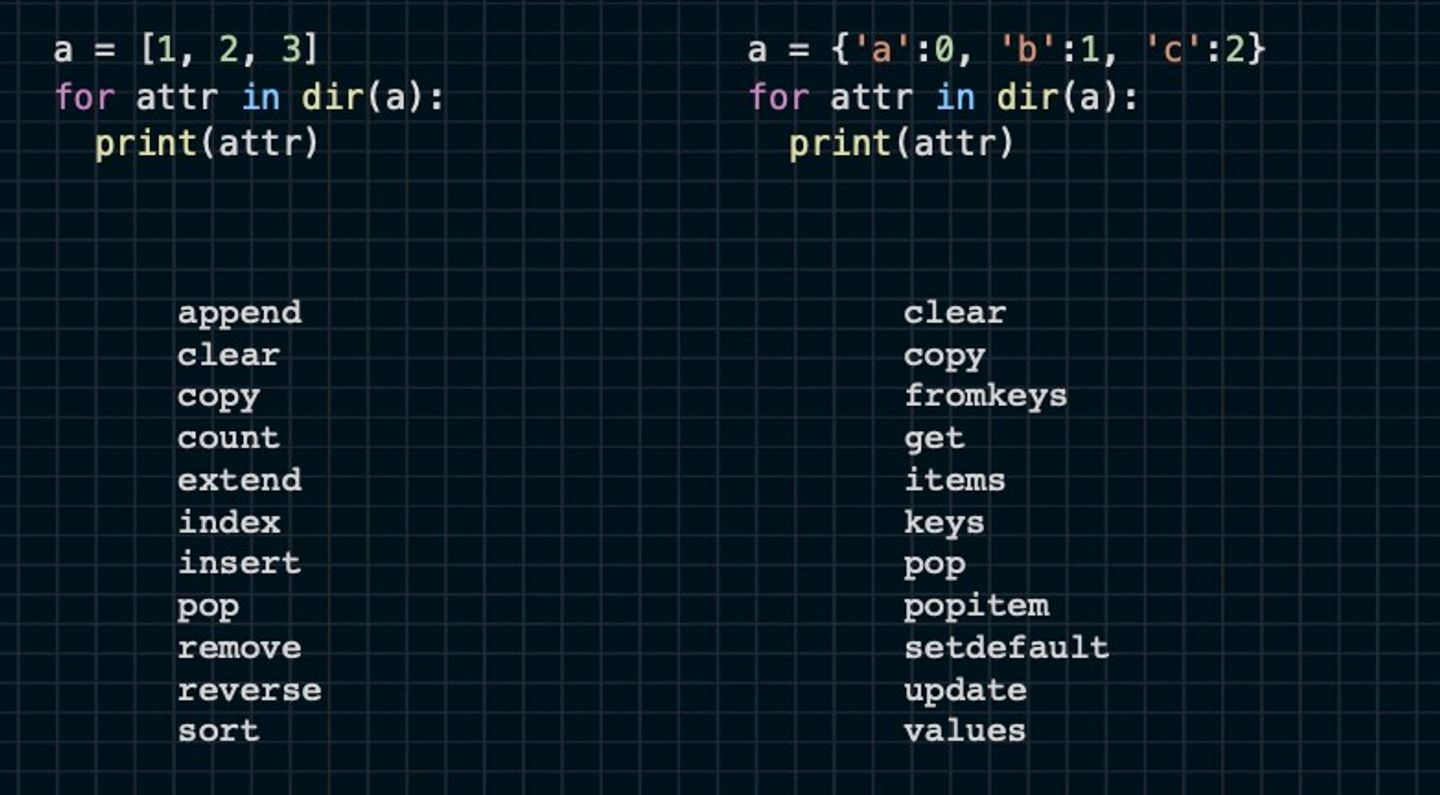
list와 dictionary 모두 특정 메서드를 지닌다는 것을 확인할 수 있음.
ndarrays Object of Numpy
ndarray Objects
import numpy as np
a = np.array([1, 2, 3])
print(type(a))
---
<class 'numpy.ndarray'>ndarray가 무엇일까? 간단하게 생각하면 편하다. 바로 numpy를 통해 연산하기 쉬운 array라고 이해하면 된다.
이 ndarray는 위에서 보여줬던 list / tuple / dictionary 보다 훨씬 많은 special method를 갖고 있다. 그 종류는 아래와 같은데, 이렇게 많은 연산을 통해 데이터의 시각화 이전의 전처리 과정에 도움을 줄 수 있다
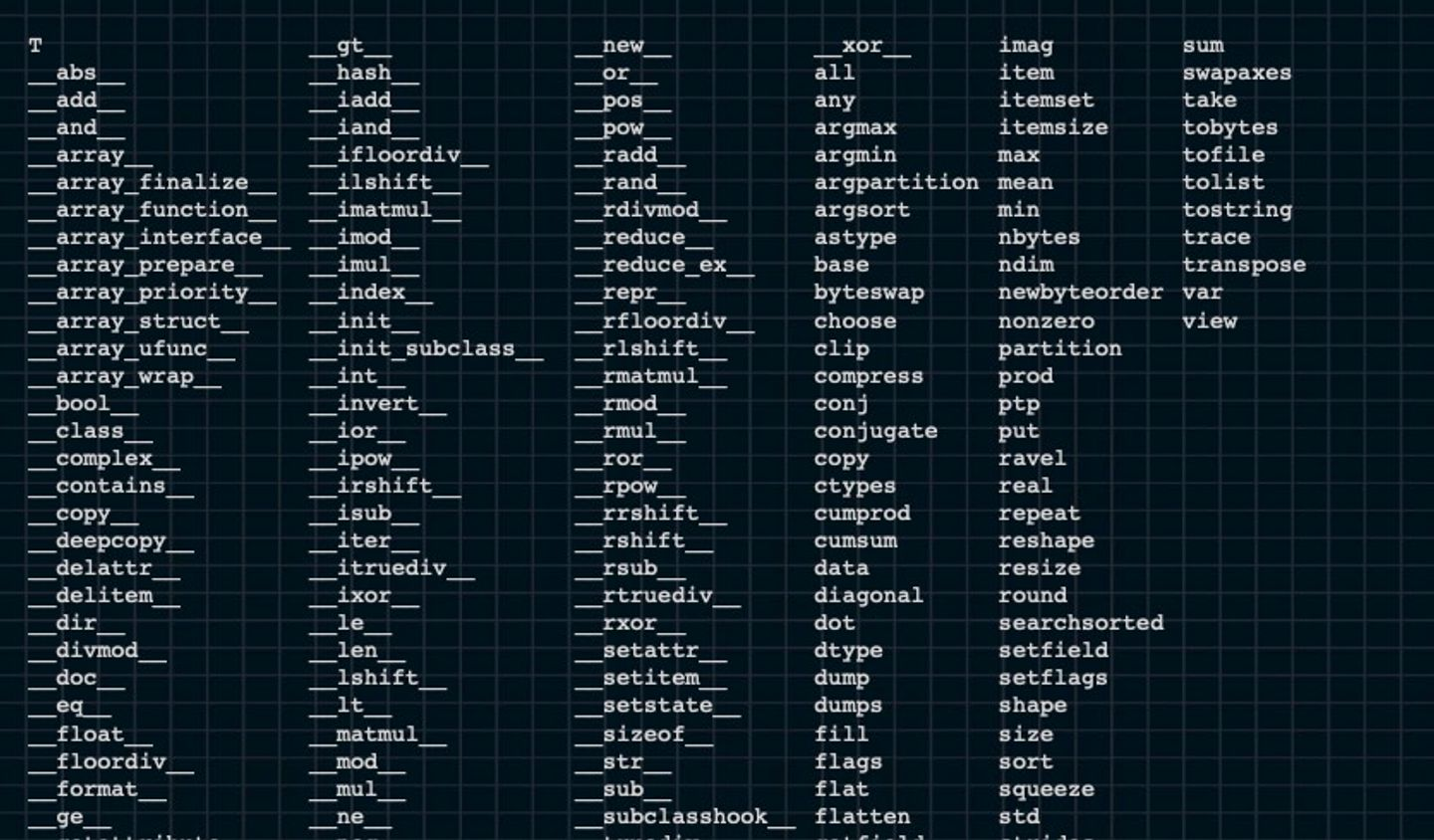
Element - wise Operations of ndarrays
얼마나 유용한지는 아래 예시를 통해 알아보자.


두 가지는 모두 같은 결과를 출력하지만 python list의 경우 for문을 통해 원소를 하나씩 더해주는 과정을 거친다.
하지만 ndarray같은 경우 array의 연산을 용이하게 도와주는 역할을 하기 때문에 데이터 시각화하기 용이한 라이브러리라고 할 수 있다.
위 두 개의 사진을 통해 알 수 있는 것은, vector와 matrix 간의 연산도 ndarray를 사용한다면 매우 간편하게 할 수 있다는 점이다.
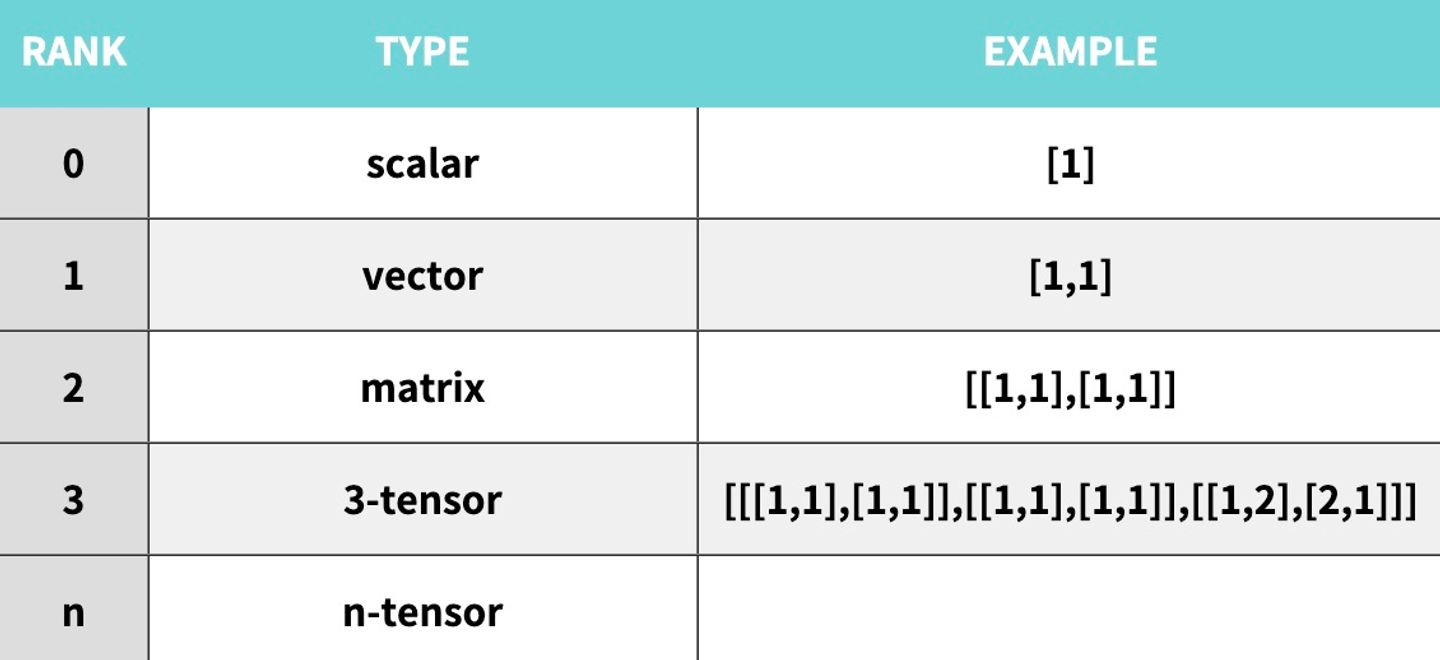
Hierarchy of Tensors
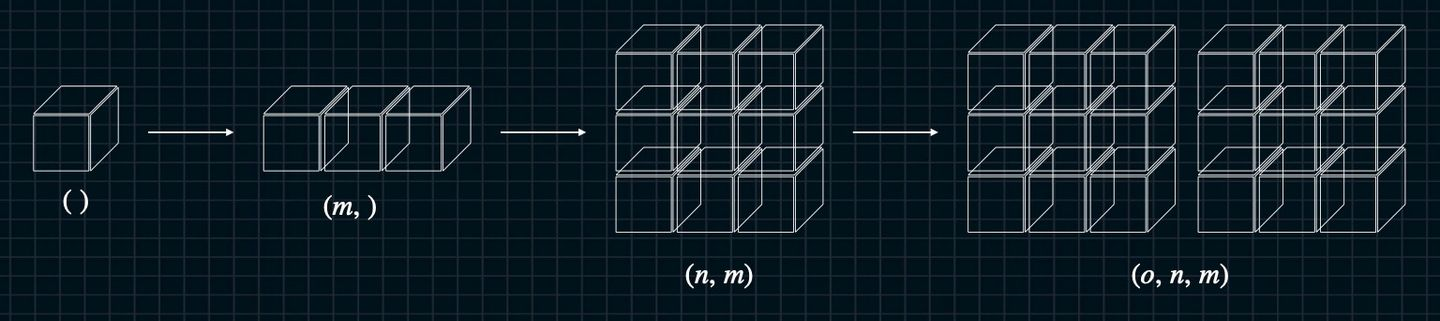
Tensor에 따라 데이터를 어떻게 연산해야 하는지도 달라진다.
0차 tensor: (), scalar 형태
1차 tensor: (m, ), vector 형태
2차 tensor: (m, n), matrix형태
3차 tensor: (m, ), 형태
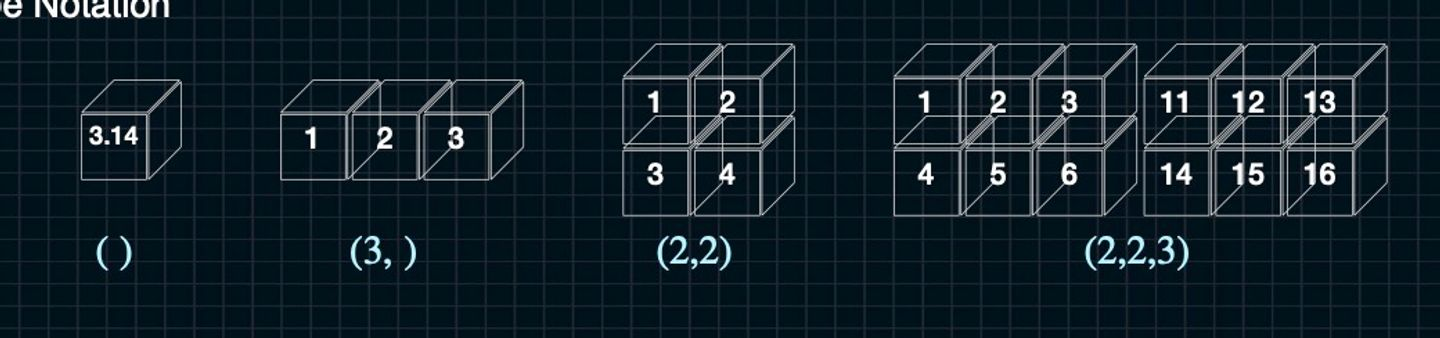
3. Making ndarray
with Shape
새로운 메서드가 보인다면 바로 검색하는 습관을 들이는 게 중요하다
- 공식 문서 확인
- 직접 하나하나 확인
- 하나하나 연습하는 과정이 필요
Shape of ndarrays
이번에 알아볼 내용은 ndarrays의 형태를 알아본다. ndarray에 대해 이론적인 부분만 알았던 나에게 큰 도움이 된 내용이다.
import numpy as np
#scalar 생성
scalar_np = np.array(3.14)
#vector 생성
vec_np = np.array([1, 2, 3])
#mat_np
ndarrays with Specific Values

numpy.full
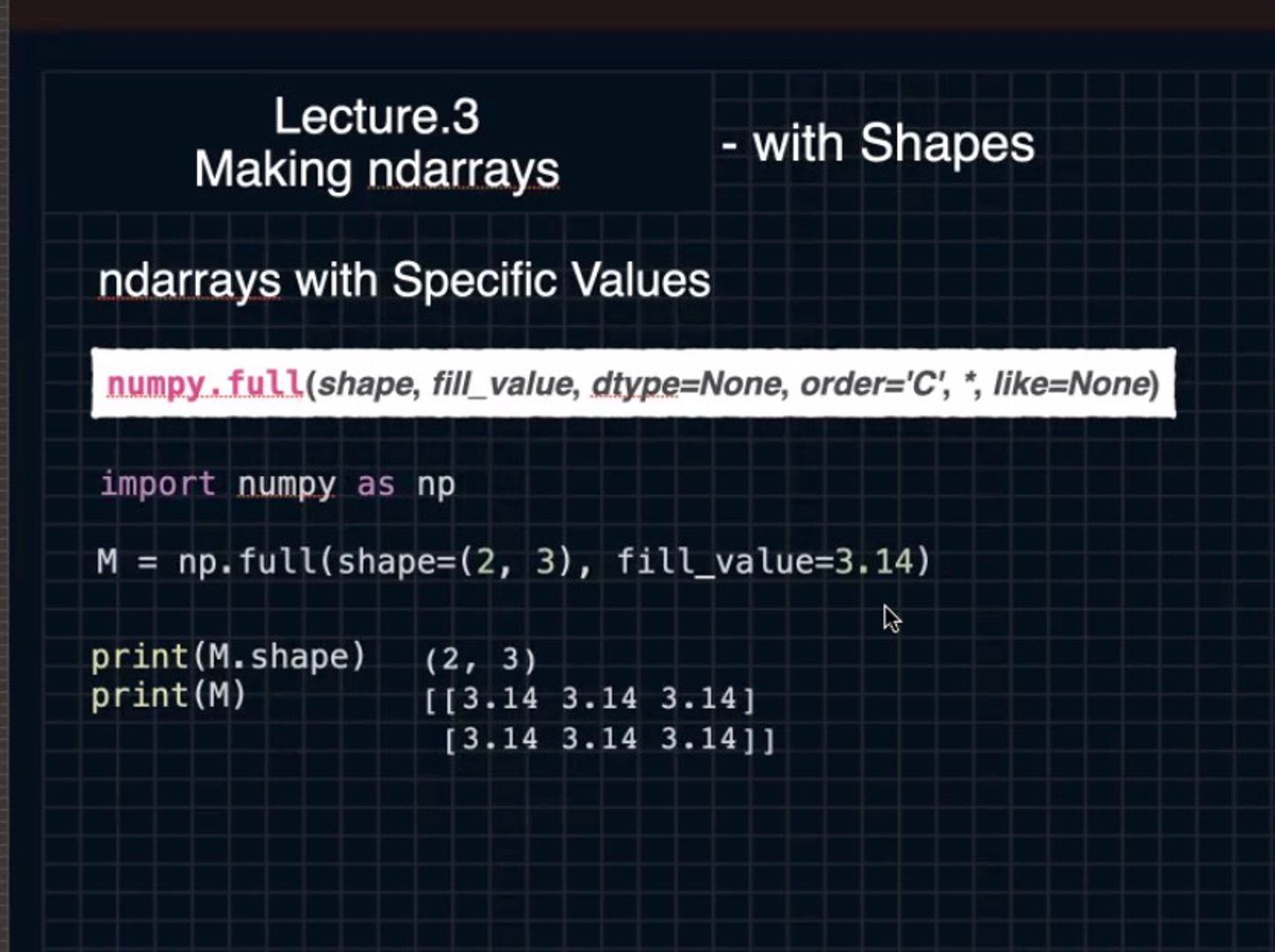
원하는 shape을 원하는 만큼 채워주는것
numpy.full(shape,fill_value,dtype=None, order='C',*,like=None)
import numpy as np
M = np.full(shape=(2, 3), fill_value=3.14
print(M.shape)
print(M)numpy.arange

numpy.arange([start]stop,[step,]dtype=None,*,like=None)
import numpy as np
print(list(range(10)))
print(list(range(2, 5)))
print(list(range(2, 10, 2)))
#얘들은 array로 처리
print(np.arange(10))
print(np.arange(2, 5))
print(np.arange(2, 10, 2))list랑 array의 차이점을 숙지할 것
import numpy as np
print(np.arange(10.5))
# [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
print(np.arange(1.5, 10.5))
#[1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5]
print(np.arange(1.5, 10.5, 2.5))
#[1.5 4. 6.5 9. ]
시작 값과 끝 값을 포함해서 값을 5개 뽑겠다는 의미
numpy.linspace(start, stop, num=50, endmpoint=True, retstep=False, dtype=None,axis=0
import numpy as np
print(np.linspace(0, 1, 5))
print(np.linspace(0, 1, 10))
]
numpy.normal

import numpy as np
#scale은 standard deviation
#np.random.normal은 정규분포값
normal = np.random.normal(loc=[-2, 0, 3], scale=[1, 2, 5], size=(200,3))
print(normal.shape)
#(200,3)numpy.randn
표준 정규분포는 데이터는 randn
randn은 표준정규분포
random.randn는 0과 1 사이에서 유니폼하게 뽑음
np.random.uniform 지정한 값에 따라 유니폼하게 뽑음
import numpy as np
import matplotlib.pyplot as plt
plt.styple.use('seaborn')np.random.randint
정수만 뽑아내는 것
import numpy as np
randint = np.randint(low=0, high=7, size=(20, ))
print(randint)
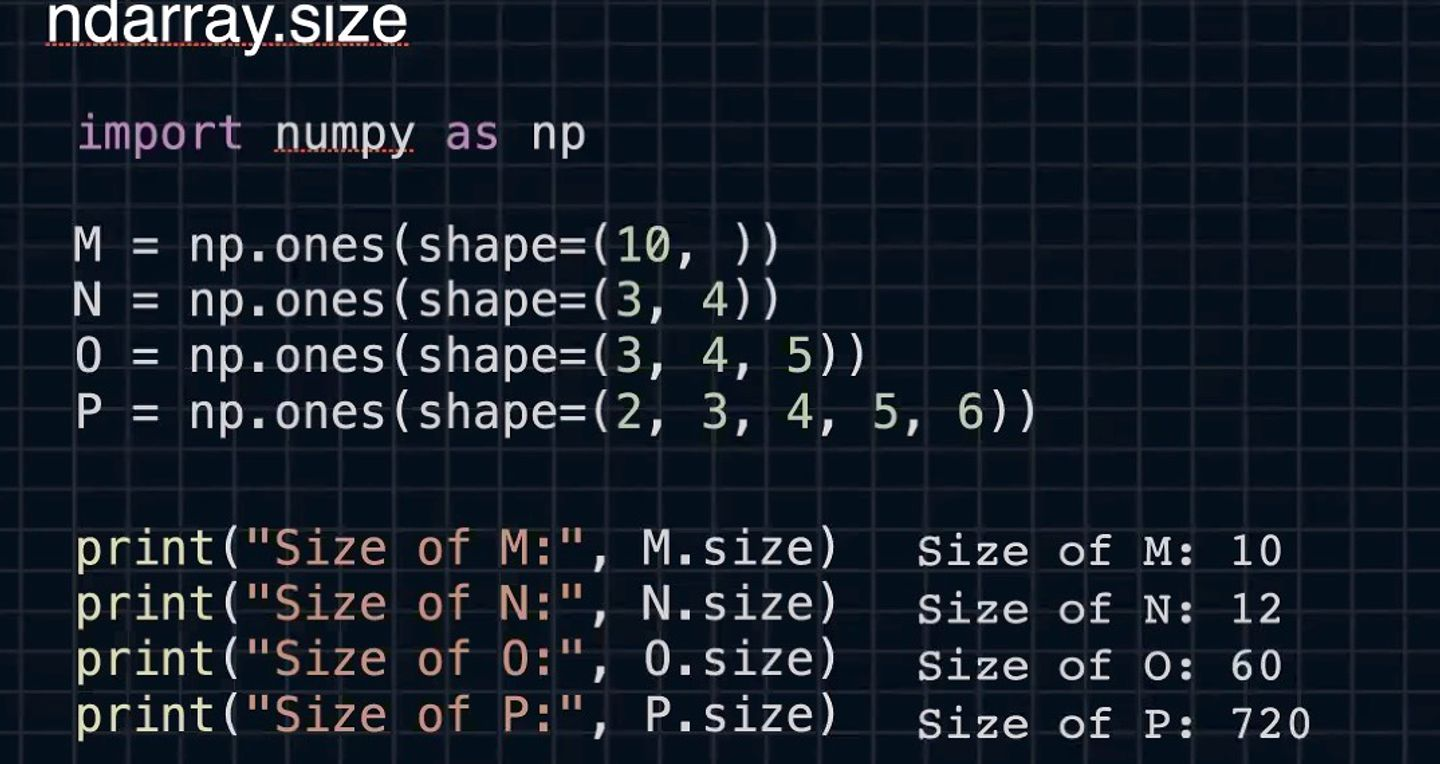
ndarray.size
size → 원소의 개수
import numpy as np
#ones: shape의 value를 전부 1로 바꿔주어 생성하는 모듈
#하나의 엑셀파일이라 생각하면 됨
M = np.ones(shape=(10, ))
N = np.ones(shape=(3, 4))
O = np.ones(shape=(3, 4, 5))
P = np.ones(shape=(2, 3, 4, 5, 6))np.reshape
size → 원소의 개수

원하는 형태로 원소 개수를 맞출 수 있어야 함
reshape은 많이 쓰이기 때문에 중요한 것
import numpy as np
a = np.arange(6)
b = np.reshape(a, (2, 3)원소의 개수가 맞다면 reshape는 언제든 할 수 있음
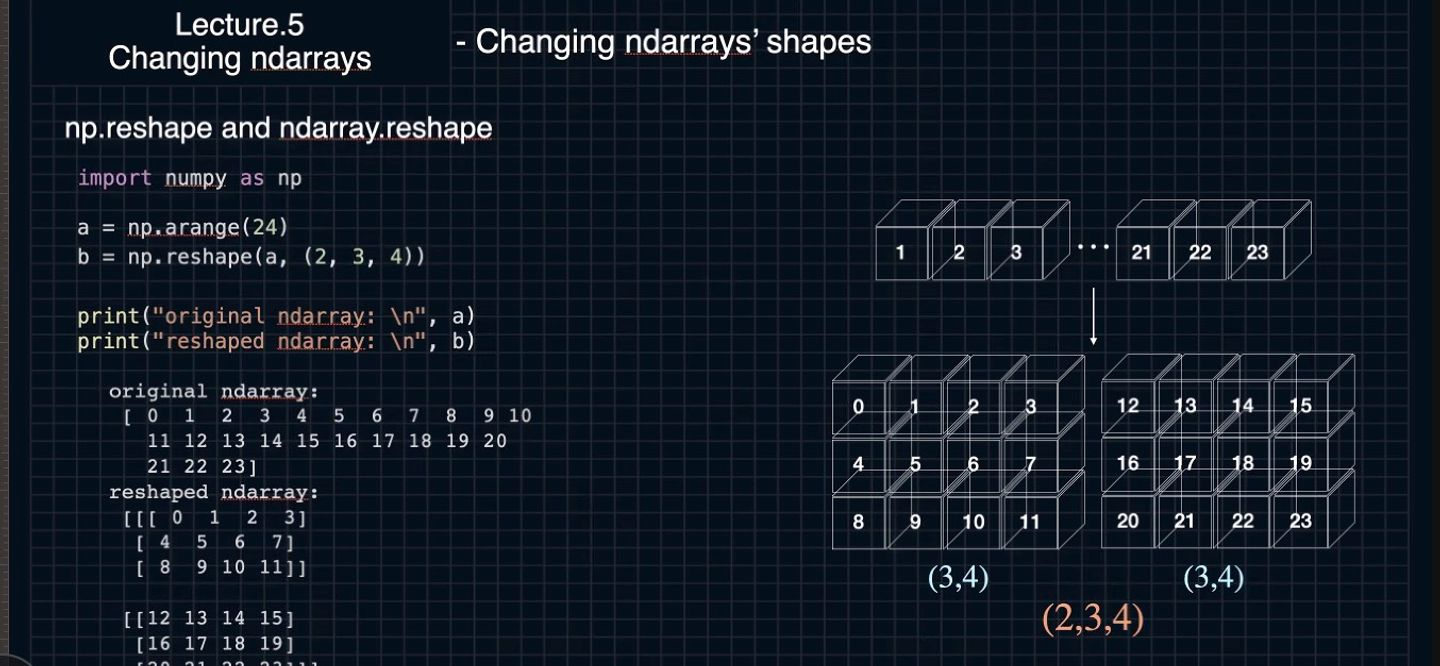
import numpy as np
a = np.arange(24)
b = np.reshhape(a, (2,3,4)
rpint(original ndarray: \n", a)
rpint(reshaped ndarray: \n", b)
- 원랜 12바이 짜리 vec
- -1?: size가 5만이라면 연산을 할 필요없이 넣으면 되니까
- b = a.reshape((2, -1))
- low
import numpy as np
a = np.arange(12)
b = a.reshape((2, -1))
c = a.reshape((3, -1))
d = a.reshape((4, -1))
e = a.reshape((6, -1))
randint를 사용해 row_vector(1, -1) / col_vector(-1, 1)
np.flatten

flatten: vector로 만들어주는 것
말 그대로 모든 요소를 1차원으로 펼쳐주는 것.
import numpy as np
M = np.arange(9)
N = M.reshape((3, 3))
O = N.flatten()
print(M, '\n')
[0 1 2 3 4 5 6 7 8]
print(N, '\n')
[[0 1 2]
[3 4 5]
[6 7 8]]
print(P, '\n')
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26]
import numpy as np
M = np.arange(27)
N = M.reshape((3, 3, 3))
O = N.flatten()
print(M, '\n')
print(N, '\n')
print(P, '\n')
넘파이를 이용하면 벡터 간의 연산을 도와준다는 것
원소 간의 연산을 자동적으로 가능하게 해줌

Broadcasting in numpy
차원이 맞지 않아도 자동적으로 계산하게 해주는 메서드
느무느무느무 중요한 메서드

이론적으로 연산이 불가능하지만 자동적으로 연산 가능하도록 shape을 맞게 해주어 원소별 연산이 가능하게 해주는 것
- 그렇다면 덧셈을 해주어야 할까?
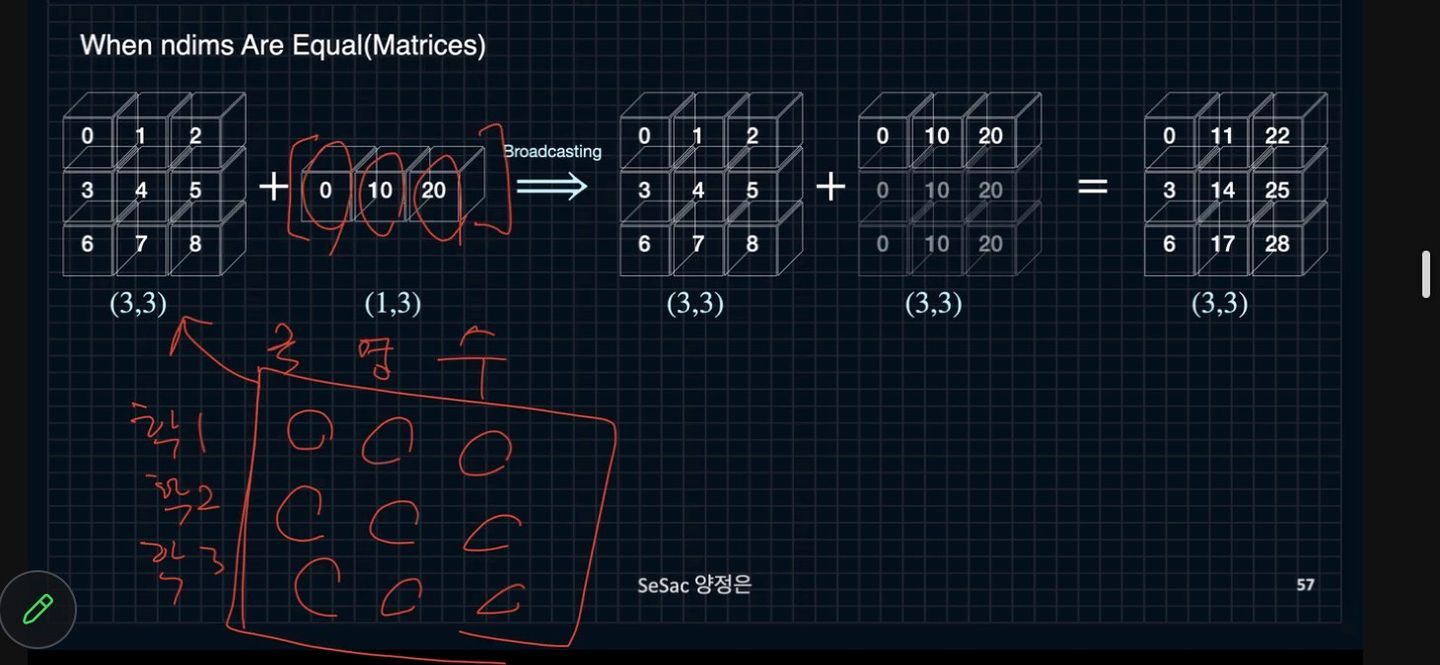
추가적으로 공통된 값을 더해주고자 할 때 이용할 수 있다import numpy as np
A = np.arange(9).reshape(3, 3)
B = 10*np.arange(3).reshape((-1,3))
C = A + B두 array의 차원이 같은 경우에만 가능
A: 2차 tensor
B: 2차 tensor
Broadcasting#2


3차원 tensor를 연산시켜주는 과정



a : scalar, 0차 tensor
u: vector, 1차 tensor

기존 방식에선 불가능하지만, numpy는 가능하다. scalar가 (5, )로 확장된다
import numpy as np
a = np.array(3)
u = np.arange(5)
print("shapes: {}/{}".format(a.shape, u.shape)
print("a: ", a)
print("u: ", u, '\n')
print("a*u: ", a*u)원소별로 가능해진다는 것이 매우 혁신적이라는 걸 인지해야 함



차원이 다른 경우 저렇게 일치한다면 matrix 끼리 연산 가능
numpy indexing and slicing

import numpy as np
a = np.arange(10)
pri
print("shapes: {}/{}".format(a.shape, u.shape)
print("a: ", a)
print("u: ", u, '\n')
print("a*u: ", a*u)



a[0] 첫번째 행이 뽑히는 것
a[0][0] 첫번째 행의 원소를 뽑는 것

