[논문] Variational Auto Encoder (VAE)

melan·2024년 3월 4일

paper_review

목록 보기

3/5

배경

큰 데이터셋이 주어졌을 때, 연속형 잠재 변수에 대해 intractable posterior distribution을 갖는 Directed Probabilistic models을 학습하는 것은 쉽지 않다. 이 문제를 해결하기 위해 많은 Mean field approach에서 posterior를 근사하는데, 근사한 posterior는 intractable한 경우가 빈번하다.

이 논문에서는 이런 문제를 해결하기 위해 먼저 intractable posterior를 근사하는 역할을 하는 probabilistic encoder $q_\phi(\textbf x|\textbf z)$ 를 포함하여 모델을 구성한다. 그리고 reparameterization trick을 이용하여 variational lower bound를 간단하고 미분 가능한 lower bound의 estimator를 만들어내는 방법을 소개한다.

아이디어 설명

원론적인 probabilistic model의 개념보다 이미지 생성 모델의 관점에서 개인적인 이해를 녹여 쓴 글이므로, 논문과 차이가 있을 수 있다.

Decoder 구조와 문제점

처음엔 $p_{\theta^*}(\textbf{z})$ 에서 continuous random variable $\textbf z$ 를 뽑는다. 그 다음, $\textbf{z}$ 를 condition으로하는 $p_{\theta^*}(\textbf{x|z})$ 분포에서 $\textbf{x}$ 를 샘플링하는 방식으로 생성형 모델이 구상되었다.

이 때 $p_{\theta^*}(\textbf{z})$ 와 $p_{\theta^*}(\textbf{x|z})$ 의 $\theta^*$ 는 True parameter를 의미하며 모든 데이터 또는 변수를 가장 잘 표현하는 상태라고 이해해도 좋다.

초기 컨셉

이 시나리오의 문제는 true parameter $\theta^*$ 를 모른다는 것이고, 더 나아가서 $p_{\theta^*}(\textbf z)$ 분포를 모르기 때문에 continous latent variables $\textbf z$ 가 어떤 값이 나올 수 있는 지 모른다는 것이다. 그리고 학습이 가능하려면 $\theta$ 와 $\textbf z$ 에 대해서 미분이 가능해야 한다.

Marginalization & Bayes’ rule

적절한 Parameter $\theta$ 를 하나의 방법은 parameter $\theta$ 를 모수로 갖는 분포가 주어진 데이터셋의 이미지인 $\textbf{x}$ 에 대해서 큰 data likelihood( $p_\theta(x))$ 를 갖도록 loss 함수를 구성하는 것이다. 그러나 $p_\theta(x)$ 를 marginalization하게 되면 $\int p_\theta(z)p_\theta(x|z)dz$ 가 된다. 이 식에서 모든 $\textbf{z}$ 에 대해서 적분하는 것이 불가능하다.

다른 전략으로는 true posterior density를 이용해서 EM algorithm을 이용한 분포 추정을 하는 것이다. 그러나 이 방법도 true posterior를 bayes’ rule에 의해 $p_\theta(\textbf{x|z})=p_\theta(\textbf{x|z})p_\theta(\textbf{z})/p_\theta(\textbf{x})$ 로 분해했을 때, $p_\theta(\textbf{x})$ 를 알 수 없기 때문에 intractable하다.

이처럼 intractable한 문제를 해결하기 위해서 true posterior를 근사하는 $q_\phi(\textbf{z|x})$ 를 정의하고 이것을 encoder로써 사용한다. 여기서 encoder는 Gaussian distribution의 형태일 것이라고 가정을 하고 true posterior와 비슷해보이도록 하는 $\phi$ 의 값을 찾게 된다.

Loss & 모델 설명

Loss 함수

$q_\phi(\textbf{z|x})$ 를 이용한 loss 함수는 다음과 같은 과정을 통해서 정의된다.

\begin{aligned} E_{z\sim q_\phi(z|x)}[log p_\theta(x)] &=E_q[log\frac{p(x|z)p(z)}{p(z|x)}]\\ &=E_q[log\frac{p(x|z)p(z)}{p(z|x)}\cdot\frac{q_\phi(z|x)}{q_\phi(z|x)}]\\ &=E_q[logp(x|z)+log\frac{q_\phi(z|x)}{p(z)}+log\frac{q_\phi(z|x)}{p(z|x)}]\\ &=E_q[logp(x|z)]-D_{KL}(q_\phi(z|x)||p(z))+D_{KL}(q_\phi(z|x)||p(z|x))\\ &\geq-D_{KL}(q_\phi(z|x)||p(z))+E_q[logp(x|z)]&& \end{aligned}

각 줄에 대한 설명은 다음과 같다.

(1): data log likelihood를 의미하는 $p_\theta(x)$ 의 기댓값을 Bayes’ rule에 의해서 풀어 쓴 것이다.
여기서 그냥 $p_\theta(x)$ 를 쓰는 것이 아니라 $log$ 를 붙여서 사용한 이유는 이후에 나오는 $q_\phi(z|x)$ 분포를 다른 분포와 함께 KL Divergence를 이용하여 표현할 것이기 때문이다.
이 이유 외에도 MLE를 할 때 log likelihood를 이용하는 경우가 많으며, $log$ 를 활용하면 곱의 형태를 합의 형태로 변형시킬 수 있다는 장점이 있다.
(2): true posterior $p(\textbf{z|x})$ 를 근사하는 $q_\phi(\textbf{z|x})$ 를 분자와 분모에 모두 곱해준 형태이다.
(3): $log$ 의 성질에 의해서 곱으로 표현된 항들을 합으로 표현한 것이다.
(4): 앞서 분수 형태로 표현된 분포들을 KL Divergence로 표현한 것이다. 이것을 통해 두 분포 간의 거리를 계산하게 된다.
참고로 여기서 사용하는 KL Divergence는 reverse KL Divergence이다. reverse가 붙은 이유는 두 분포의 순서가 바뀌었기 때문인데, 한번쯤 읽어보는 것이 좋다.
(5): $D_{KL}(q_\phi(z|x)||p(z|x))$ 항이 양수라는 특징 때문에, 남은 두 항의 합이 (4) 식보다 작다는 것을 표현한 것이고 이것이 ELBO(Evidence Lower BOund)가 된다. 이것이 최종적인 loss 함수이고 이것을 최대화하는 방향으로 학습이 진행된다.
(4) 식에서 $D_{KL}(q_\phi(z|x)||p(z|x))$ 항이 intractable 하지만 KL Divergence 특성 상 항상 양수가 된다. 해당 항이 intractable한 이유는 true posterior $p(z|x)$ 분포는 directed graphical model의 특성 상 알아낼 수 없기 때문이다.

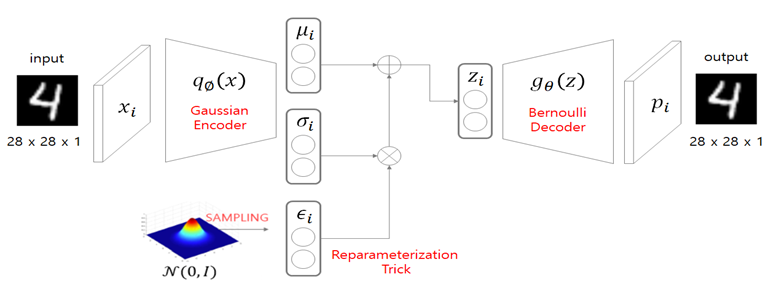
모델 구조

위 그림에서 살펴볼 만한 점은 encoder( $q_\phi(x|z)$ ) 부분이다. Continuous latent variables $z_i$ 를 Gaussian으로 가정을 하기 때문에 해당 분포의 모수에 해당하는 $\mu, \sigma$ 를 추론하는 encoder로 만든 것이다.

이외에 주목해야 하는 부분은 reparameterization trick 부분이다. 분포를 만들고 거기서 샘플링한 $z$ 를 이용하게 되면 $\mu, \sigma$ 에 대해 미분하는 것이 어렵다. 이런 문제를 해결하기 위해 적용된 것이 reparameterization trick이다. 먼저 $\mathcal{N}(0, I)$ 에서 하나의 값을 샘플링( $\epsilon_i$ )하고, 이 값에 표준편차를 곱한 후( $\sigma_i \epsilon_i$ ) 평균을 더하여( $\mu_i+\sigma_i \epsilon_i$ ) 실제 분포에서 샘플링한 것과 동일한 값을 만들어준다. 이렇게 표현한 값은 $\mu$ 와 $\sigma$ 의 선형 결합이기 때문에 미분이 가능해서 미분 가능한, 즉 학습이 가능한 형태가 된다.