ResNet

Abstract

신경망의 깊이가 깊어질 수록 정확도를 높이는데 도움이 되지만, 깊어질 수록 학습시키기 어려워진다. ResNet은 residual learning framework를 이용해서 앞선 연구보다 깊은 신경망을 만들었다. residual function은 함수의 입력을 다시 참조하는 구조이다.

이 구조는 최적화가 더 쉽고, 깊이를 상당히 늘려서 높은 정확도를 얻을 수 있다. VGGNet보다 8배 더 깊은 152 layer로 구성했으며, 이 모델을 앙상블 해서 ImageNet dataset을 학습시켰을 때 3.57%의 에러를 달성했다.

1. Introduction

깊은 신경망은 여러 수준의 feature(논문에서는 low/mid/high-level feautures라고 표현함)와 분류기로 구성되어 있고, feature의 수준은 신경망의 깊이가 깊어질 수록 풍부해진다. 많은 연구에서 깊이가 중요한 요소임을 많이 보였고, 여러 곳에서 깊은 신경망을 이용하고 있다.

하지만 깊은 신경망을 학습이 쉽지 않다. 학습이 쉽지 않다는 것은 weight가 괜찮은 상태에 안정적으로 수렴하지 못한다는 것인데, 이것을 발생시키는 대표적인 문제가 vanishing/exploding gradient 문제이다. 하지만 이 문제들은 초기화와 정규화 기술로 어느 정도 해소되었다.

이 문제가 끝나고 degrading 문제가 나왔다. 깊이를 늘릴 수록 어느 지점부터 정확도가 줄기 시작했는데, 문제는 overfitting이 아니라는 것이다.

이 논문에서, deep residual learning framework를 이용해서 degrading 문제를 해결했다. 몇 개의 layer를 바로 연결하는 것 대신에 residual mapping이라는 것을 한다.

구조는 위와 같다. $F(x)$는 기존의 것과 동일하고 여기에서 identity라고 하는 x를 추가하는 것이다. 이 연결을 “shortcut connection”이라고 하고 이것이 추가된 것이 그렇지 않은 것에 비해서 학습이 쉽다고 이야기한다.

3. Deep residual learning

3.1 Residual Learning

Degrading 문제는 단순한 multiple nonlinear layer만을 이용해서 입력과 동일한 출력을 만들어 내는 것이 어렵다는 것을 보인다. 만약 identity mapping이 최선이라면, multiple nonlinear layer는 0에 가까운 값을 출력하면 된다.

실제로 identity mapping을 하는 것이 최선은 아니지만 도움이 된다. 만약 최적의 함수가 zero mapping보다 identity mapping에 가깝다면, 학습하는 과정에서 identity mapping을 기준으로 미세한 변화를 감지할 수 있다.

논문에서 언급하는 내용이지만 Residual의 학습이 더 쉬운 이유가 직관적으로 이해되지 않아서 더 찾아본 내용을 적어보겠다.

Weight layer를 통과한 결과값이 $H(x)$라고 할 때, $H(x)$가 $x$와 유사한 값이라고 가정해보자. (이 가정이 성립하는 이유는 이후에 설명). 이런 결과값을 만들어 내는 방법은 크게 두 가지가 있다.

1. $H$가 identity matrix이다.
2. $H(x)$가 0에 가까운 값이고 $x$를 더해준다.

ResNet은 이 두 방법 중 후자를 선택한 것이다.

가정($H(x)$는 $x$와 가까운 값이다.)에 대해서 이야기하겠다. 깊은 신경망이 단 몇 회 만에 loss를 급격하게 줄이는 방식으로 학습을 한다면, 이것은 weight를 크게 조절하는 것이고 이것은 test set에 대한 좋은 일반화 성능을 기대하기 어렵다.

따라서 (일반 신경망도 그렇지만) 깊은 신경망일 수록 점진적으로 값을 조절해야 하고, 점진적으로 변해간다면 어떤 블록의 입력값 $x$와 출력값 $H(x)$의 차이는 크지 않을 것이라는 것이 핵심 아이디어이다.

차이가 크지 않을 것이기 때문에, residual mapping 없이 입력값 $x$를 넣어서 “$x$ 근처의 값”을 생성해내는 weight를 계산하는 것보다, identity $x$를 더하고 편차(residual)에 해당하는 0 근처의 값을 생성해내는 weight로 맞추는 것이 더 쉬운 task라는 것이다.

3.2 Identity Mapping by Shortcuts

Shortcut connection을 추가한다고 해서 parameter의 수가 늘거나 computation complexity를 늘리지 않는다.

Shortcut connection을 이용해서 identity mapping을 해주는 것만으로도 degrading 문제를 해결할 수 있다.

연산 중간에 matrix $W_s$를 사용하는데, 이것은 연산 과정에서 conv layer의 stride를 2로 설정해서 feature map의 크기를 변경하게 되면 identity도 크기를 맞추기 위함이다. 성능은 shortcut connection만으로 향상된다.

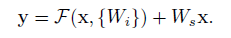
3.3 Network Architectures

Plain Network는 VGGNet을 바탕으로 몇가지 사항을 수정하였다.

1. 각 레이어는 동일한 크기의 feature map을 만들기 위해서 같은 개수의 필터를 이용한다.
2. feature map의 크기가 반으로 줄게 되면 필터의 개수를 2배로 늘린다.

또한 downsampling을 할 때는 filter의 stride를 2로 설정하여 줄인다. 마지막에는 global average pooling을 해서 1000종 분류를 한다.

이런 구조는 기존의 VGGNet보다 적은 필터를 사용하며 낮은 복잡도를 갖는다.

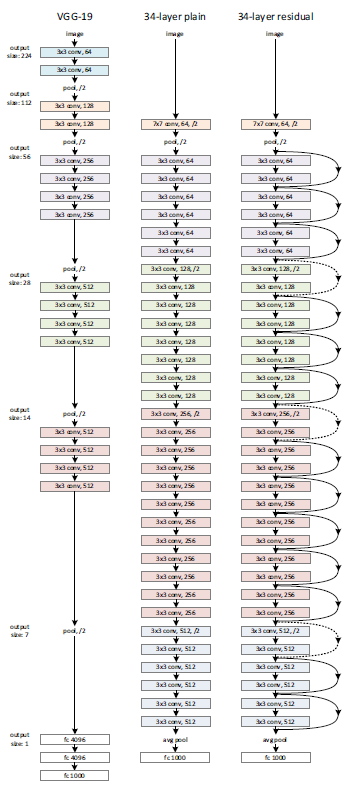
Residual Network는 VGGNet을 기반으로 만든 plain network에서 shortcut connection을 추가한 형태이다.

shortcut connection은 identity와 feature map의 크기가 같으면 그냥 더해지지만, 차원이 증가하면 다음 두 옵션 중 하나를 선택해서 수행한다.

1. 0으로 구성된 패딩을 추가해서 단순하게 차원의 수만 맞춘다.
2. 1x1 convolution을 이용해서 차원을 늘린다.

3.4 Implementation

• Image resize: [256, 480] 사이의 값 random sampling하여 이미지의 짧은 부분 rescale
• crop: rescaled image에서 224x224 크기의 crop을 무작위 추출 후 horizontal flip. 각 픽셀의 평균값을 빼준다. color augmentation 이용한다.
• Batch Normalization(BN): convolution → BN → activation 순으로 적용
• Weight initialization: ???
• SGD
  • batch size: 256
  • LR: start=0.1, error plateaus에서 10씩 나누기
  • epochs: 60 * 10^4
  • weight decay (regularization): 0.0001
  • momentum: 0.9
  • dropout: X

Testing에서는 10-crop testing을 했고 fully convolutional을 이용했다. 또한 여러가지 scale에 대해서 average score를 이용해서 평가를 진행했다.

4. Experiments

Plain and ResNet

Layer의 수가 동일한 상황에서 plain보다 ResNet가 더 낮은 train error를 보였다.

Plain에서 깊이만 변화시켰을 때, lyaer가 많아질 수록 더 높은 train error가 나왔다.

반면에 ResNet에서 깊이만 변화시켰을 때, layer가 많아질 수록 train error가 낮게 나온다.

깊이가 깊지 않다면 plain도 괜찮은 솔루션을 만들어내지만, 이 경우에서도 ResNet이 더 적게 반복하고 빠르게 최적에 수렴하게 된다.

Identity vs. Projection shortcuts

ResNet의 구조를 보면 중간에 convolution의 stride를 2로 설정하여 크기를 줄임과 동시에 필터의 개수를 2배로 사용해서 차원의 수를 늘린다. 이 과정에서 고려해야하는 것이 shortcut으로 들어가는 입력의 차원 수를 늘려줘야 한다는 것이다.

만약 입력의 차원이 $n$이고 shortcuts으로 전달해야하는 차원의 수가 $2n$이라고 할 때, 차원의 수를 늘리는 방법은 세 가지가 있다.

(a) zero-padding shortcuts: 부족한 차원의 수($n)$만큼을 0으로 채워서 전달하는 방법이다.

(b) projection shortcuts: 부족한 차원의 수($n$) 만큼을 1x1 convolution으로 만들어서 전달한다.

(c) all shortcuts are projections: 기존의 입력을 1x1 convolution에 넣어서 $2n$개의 새로운 값을 만들고 전달한다.

3가지 방법을 모두 시도했을 때 a, b, c 순으로 성능이 좋았다. 하지만 이 방법이 degrading 문제를 해결하는데 필수적인 부분이 아니고 b와 c의 성능 차이가 크지 않으며, b보다 c가 더 많은 자원을 이용한다는 점에서 논문에서는 (b) 방법을 채택했다.

Deeper Bottleneck Architectures

학습 시간의 문제 때문에 블록의 구조를 Bottleneck design으로 변경했다.

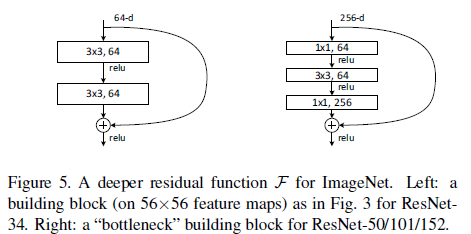
Bottleneck구조는 Fig 5의 오른쪽과 같은 형태이다. 위 아래로 있는 1x1 convolution은 차원의 수를 줄이고 다시 복원하는 역할을 한다. Fig 5에서 표현된 블록의 차원 수를 보면 왼쪽은 64개의 차원을 계산하는 것이고 오른쪽은 결과적으로 256개의 차원을 계산한 것과 같은 효과를 내는데, 이 두 구조는 비슷한 time complexity를 갖는다.

50-layer ResNet

기존의 2-layer 블록으로 구성된 ResNet은 34-layer이다. 이 블록을 bottleneck 구조의 블록으로 변경하면 50-layer ResNet이 된다. 앞서 말한 것과 같이 shortcut의 차원을 늘려줄 때에는 projection에서 option B를 이용한다.

101-layer and 152-layer ResNet

50-layer와 마찬가지로 3-layer 블록을 이용해서 101-layer와 152-layer ResNet을 만들었다. 두 가지 구조 모두 VGG-16/19 보다 낮은 복잡도를 갖는다.