문제 설명

N으로 3*2^K (0 <= k <= 10)인 수가 들어온다.
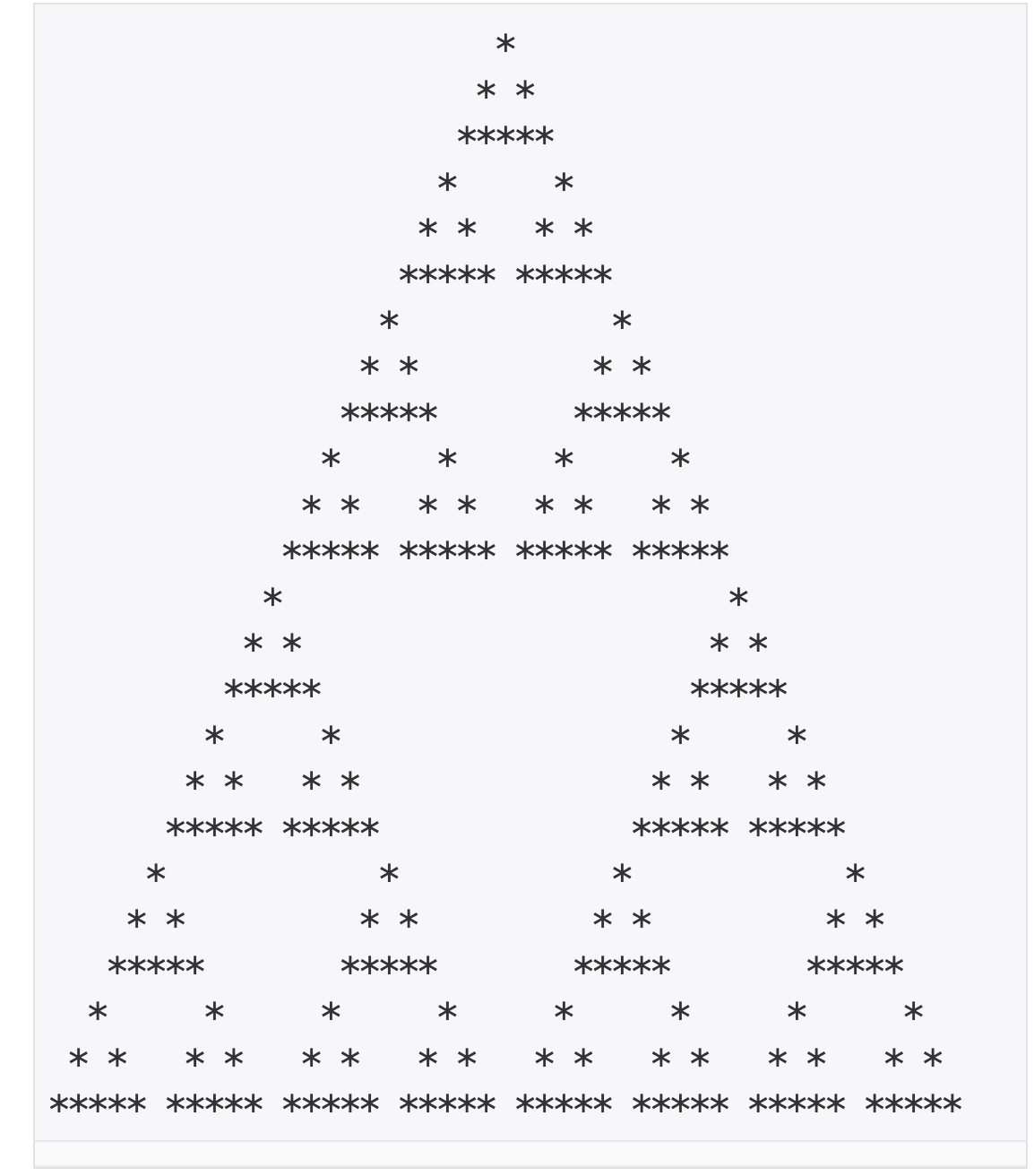
이때, 다음과 같은 패턴을 만족하도록 출력해라. 아래 예시는 N이 24인 경우다.

문제 접근

처음엔 재귀로 하려했으나, 재귀로 하면 중간 중간에 DP로 저장하지 않는한, 반복적인 탐색이 존재해서 비효율적이라고 생각했다. 예를 들어 생각해보자. 이전 과거의 탐색에서 만약 k가 3인 경우의 삼각형을 찾았다면 다른 탐색들에서는 k가 3인 삼각형에서 k가 2인 삼각형을 찾기 위해 다시 재귀를 할 필요가 없어야 한다는 것임(왜? 과거에 나는 이미 k가 3인 경우에 대해 재귀를 통해 구한 경험이 있으므로). 하지만, 이를 위해 dp를 적용해서 사이즈가 다른 삼각형들의 모양을 기억하는 것은 코드가 복잡해지며 메모리 낭비라고 판단했다.

때문에 이전에 배웠던 슬라이딩 윈도우 기법을 적용(이제보니 온라인 알고리즘이라고 말하는게 더 정확해보인다)했다. 다음과 같이 하면 메모리와 시간 양쪽에서 모두 이득이라고 생각했다.
방법은 다음과 같다.

(형광색 친 곳은 leftStart와 rightEnd의 초깃값이 가리키는 열임)

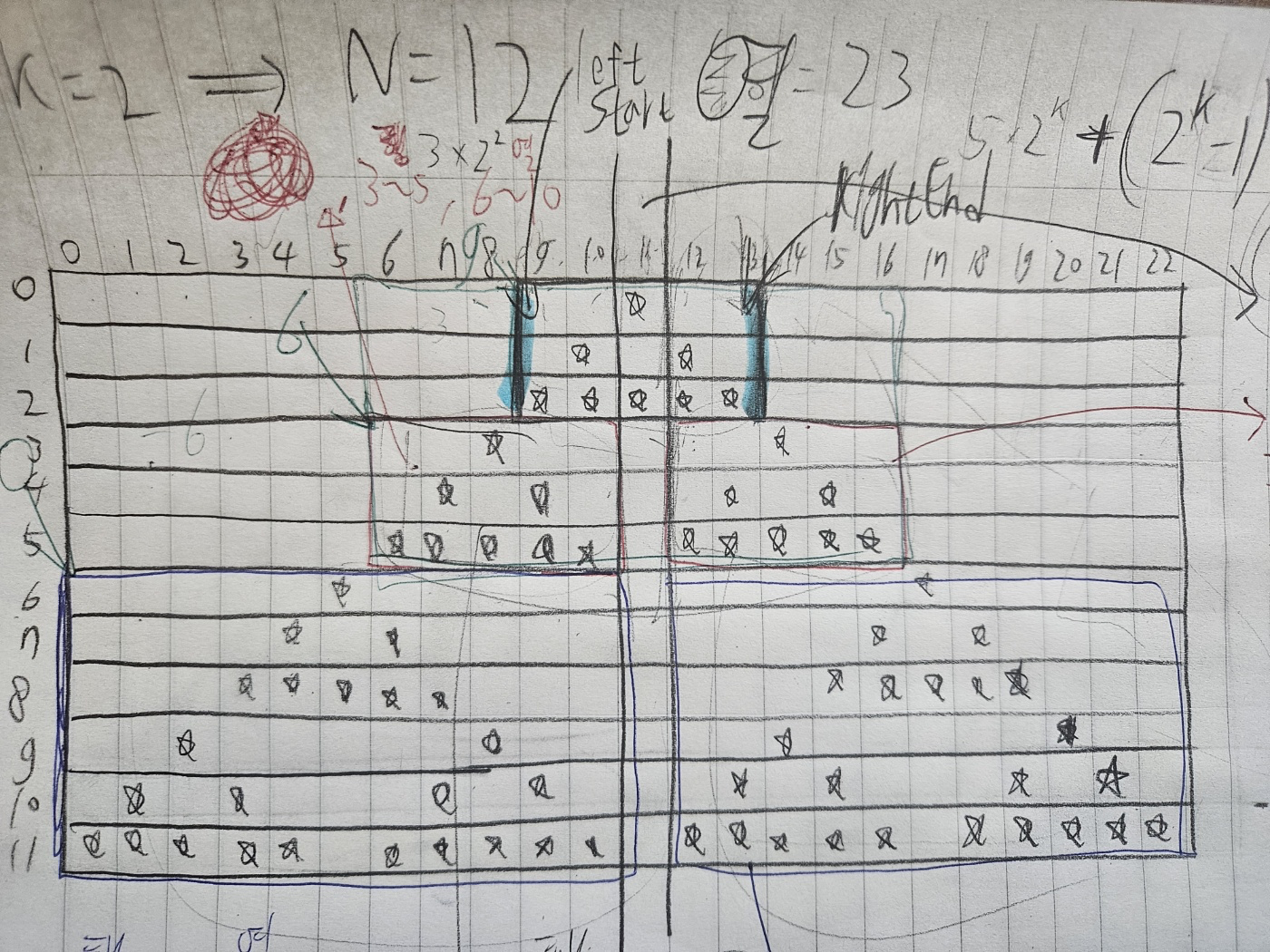
우선, 입력받은 N으로부터 k를 찾고, 이를 활용해서 전체 배열의 행,열 크기를 찾는다.
그리고 배열을 준비한다.
k=0이상이므로 항상 N은 3이상이다. 따라서, 우선적으로 가로크기5, 세로크기3의 박스를 배열 중간|위쪽에 배치하고 이 안에 삼각형을 그린다.
그리고 이 삼각형의 왼쪽을 leftStart, 오른쪽을 rightEnd로 지정한다. 그리고 topRow를 현재까지 구한 삼각형의 행크기인 3으로 설정한다.
그리고 k번 반복문을 반복한다. 위 그림에서는 k가 2다.

처음반복에는, 3~5까지의 행에 좌우로 삼각형 두개를 복붙한다. 이 삼각형은 바로 행0~topStart-1까지 그려진 삼각형이다.
그리고 leftStart와 rightEnd, 그리고 topStart를 갱신한다.

그리고 두번째 반복에서도 0~topStart-1까지의 행에 그려진 삼각형을 6~11까지의 행안에 좌우로 복붙한다.
이렇게 되면 우리는 포인터들만 기억하고, 추가적인 메모리 공간을 전혀 사용하지 않으며, 함수 콜 스택도 쌓이지 않는다.

풀이

import java.util.*;
import java.io.*;

public class Main {

    static int N;
    static char[][] stars;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        int rowSize = N;
        int k = findK(N);
        int colSize = 5 * (int) Math.pow(2, k);
        colSize = colSize + (colSize / 5 - 1);

        stars = new char[rowSize][colSize];
        for (int i = 0; i < rowSize; i++) Arrays.fill(stars[i], ' ');

        int center = (colSize - 1) / 2;
        int leftStart = center - 2;
        int rightEnd = center + 2;

        stars[0][center] = '*';
        stars[1][center - 1] = '*';
        stars[1][center + 1] = '*';
        for (int i = leftStart; i <= rightEnd; i++) {
            stars[2][i] = '*';
        }

        int topStart = 3;
        int curLeftStart;
        int curRightEnd;
        int curBottomRow;

        for (int i = 1; i <= k; i++) {
            curLeftStart = leftStart - topStart;
            curRightEnd = rightEnd + topStart;
            curBottomRow = 2 * topStart - 1;

            for (int ri = 0; ri < topStart; ri++) {
                for (int ci = 0; ci < rightEnd - leftStart + 1; ci++) {
                    stars[topStart + ri][curLeftStart + ci] = stars[ri][leftStart + ci];
                    stars[topStart + ri][center + 1 + ci] = stars[ri][leftStart + ci];
                }
            }

            leftStart = curLeftStart;
            rightEnd = curRightEnd;
            topStart = curBottomRow + 1;
        }

        // 결과를 출력한다.
        for (char[] row : stars) {
            System.out.println(row);
        }
    }

    static int findK(int n) {
        int temp = n / 3;
        int k = 0;
        while (temp != 1) {
            temp /= 2;
            k++;
        }
        return k;
    }
}

오오... 적어도 자바 11 기준으로는 내가 최근 모든 풀이 중에 메모리와 시간이 가장 적다... 이런적이 처음이라 자랑을 조금만 하고싶다. 그동안 백준 공부했던게 조금씩 효과가 나오고 있는 것 같다. 슬라이딩 윈도우 기법은 매우 효율적이다 bb
수정) 그런데, 이제보니 dp가 더 가까운듯 싶다. 메모리를 추가적으로 안쓰는 DP 라고 봐야할듯. 그리고 슬라이딩 윈도우보다는 더 넓은 범주인 온라인 알고리즘이 맞는듯 싶다.