아직 학생이기도하고 영어가 미숙하다보니 본 리뷰에 오류가 있을 수도 있습니다. 이 점 감안해주시고 혹시나 찾으신다면 피드백 감사히 받겠습니다.
Introduction
View syntheis에 대한 수많은 연구들이 있어왔지만, 해당 연구에서 연구진은 5D scene representation를 기반으로 parameter들을 조절하며 여기에 Volume Rendering을 적용해 View Synthesis를 구현했습니다.
연구진은 한 정적인 장면을 Color 값과 density를 output으로 뱉는 5D 함수로 표현했습니다. 이때 5D 함수의 input는 위치와 방향 으로 이루어져있습니다. 각 위치의 density 값은 해당 위치를 통과하는 빛의 양에 따라 radiance가 얼마나 얻어지는지를 나타냅니다. 즉, 연구진의 방법은 위치와 방향을 나타내는 5D 좌표로부터 single volume density와 view 기반의 RGB color를 추정합니다.
NeRF는 다음과 같은 과정을 통해 rendering됩니다. 우선 해당 시점으로부터 목표로하는 image의 pixel에 camera ray를 march시킵니다. 그 후, 해당 ray가 통과하는 3D point들의 sample set을 형성한 후, 해당 점의 좌표와 ray의 direction을 Neural Network에 input으로 넣어 색과 density 값과 color 값을 얻어냅니다. 그 후, classical volume rendring 기법을 통해 해당 값들을 기반으로 2D image를 생성해냅니다. 이러한 과정들은 모두 differentiable하기 때문에 gradient des들ent algorithm을 이용해 쉽게 optimize할 수 있습니다. 아래 사진은 위 과정을 그림으로 보여주고 있습니다.
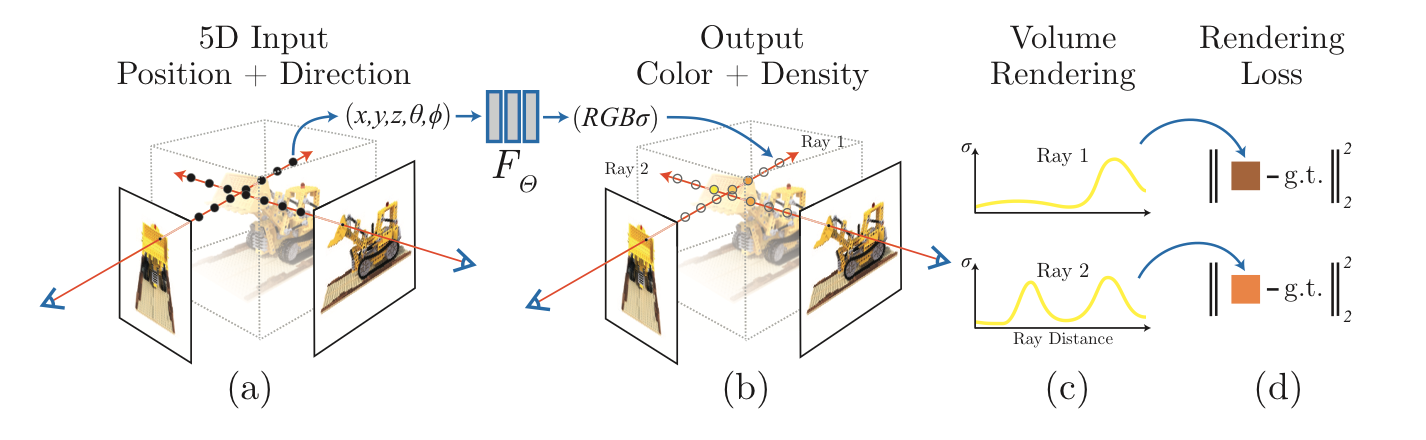
하지만 연구진은 이러한 단순한 neural radiance field의 표현법은 고해상도의 image를 출력하기는 어렵다는 사실을 알게 되었습니다. 따라서 positional encoding 기법과 또한 hierarchical sampling 과정을 통해 MLP만으로 좀 더 고해상도의 image를 표현할 수 있게 하였습니다.
Neural Radiance Field Scene Representation
연구진은 5D vector-valued function으로 연속적인 장면을 표현하고 있습니다. 이 5D vector의 input은 크게 location 과 2D viewing direction 으로 구분되고,output은 color 와 volume density 로 구분됩니다. 사실 함수 내부에서 view direction에 관한 input은 3D Cartesian unit vector 로 표현되기 때문에 사실상 6개의 input을 지닌 함수라고 표현해도 될 것 같습니다. 이렇게 최종적인 식은 로 표현을 할 수 있습니다.
또한 multiview에서 consistent한 image를 생성하기 위해 density 의 경우는 location input인 의 영향만 받게 하고, color는 모든 input의 영향을 다 받도록 설계하였습니다.
여기서 Radiance Field라는 개념을 이해하기 위해 저는 다음과 같이 해석했습니다. ray가 생성한 점들의 집합에 대해 해당 점은 다양한 ray가 지날 수 있을 것입니다. 그렇기에 각 점은 지나는 빛의 방향에 따라 다양한 radiance를 가질 것이고, 그 radiance를 distribution으로 표현이 가능하다는 점에서 NeRF에 네이밍이 Neural Radiance Field가 아닐까 해석하였습니다. 아래 그림에서는 한 점에서의 radiance distribution을 확인할 수 있습니다. 사실 위에서 표현한 color라는 표현이 결과론적이고 실제로는 radiance로 표현을 하는 것이 좀 더 올바르지 않을까라는 생각도 하였습니다.
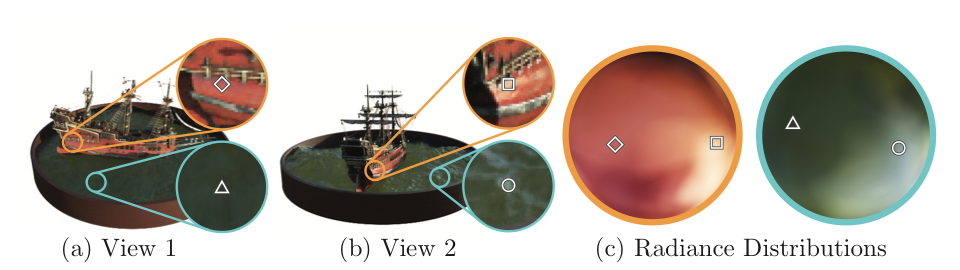
Volume Rendering with Radiance Fields
연구진의 5D NeRF는 한 장면을 volume density와 directional emitted radiance(위에서는 color로도 표현)로 표현하였습니다. 빛의 색은 빛이 뚫고 지나가는 장면들에 대해서 volume rendering을 기반으로 정해지며, 해당 과정에서 volume density는 각 x마다의 빛이 종료될 확률분포를 의미한다고도 해석될 수 있습니다. 그리고 해당 ray의 예측되는 색은 다음과 같은 수식으로 표현됩니다.
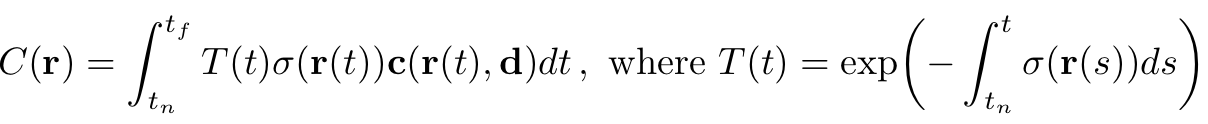
본 식에서 로 해석되고 t의 범위인 near한 곳부터 가장 far한 곳 까지 지나가는 ray의 범위를 의미합니다.
또한 여기서 유의해야할 점은 식입니다. 해당 식은 Density에 대한 constraint function으로 해석을 하였는데, 어떠한 점이 존재할 때 ray가 그 점에 닿기 전까지 지나온 점들의 Density값을 조사해 해당 점이 최종 색의 영향을 끼치는 결과를 어느정도 반영하는 식이라고 생각하였습니다. 예를 들자면 Density가 0.5인 두 점이 존재할 때 하나는 앞의 존재하는 점들의 density가 평균적으로 0.1이고 한 점은 평균적으로 0.9일 때 해당 점들이 최종 color 결과에 기여하는 정도는 다를 것이기 때문에 해당 정도를 조절하는 식 정도로 생각하면 될 것 같습니다.
하지만 이러한 연속적인 식은 MLP가 이산적인 결과값을 제공하고 이미지와 Voxel 역시도 이산적인 data이기 때문에 Integral 기반의 식을 사용하는데 문제가 생길 수가 있어서 식을 이산형으로 변환합니다. 우선 를 N으로 공평하게 나누어서 계산을 실시하는데 이러한경우 각 는 다음과 같이 표현이 가능합니다.
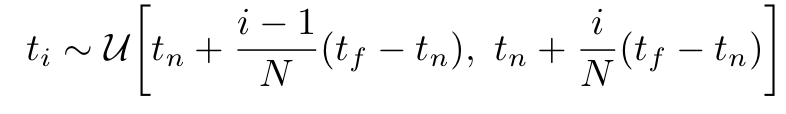
또한 위에서 언급했던 역시도 적분이 시그마로 바뀌면서 다음과 같은 식으로 표현 될 수 있습니다. 이 과정에서 density에 대한 식에 변형이 있었는데 이 부분은 Volume Rendering에 대한 개념으로 차차 알아가는 대로 수정하도록 하겠습니다.
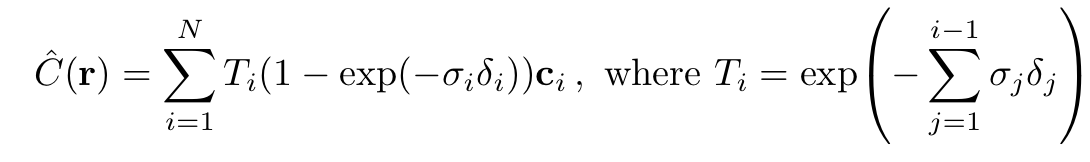
Optimizing a Neural Radiace Field
위와 같은 식으로 NeRF를 구현할 수 있었지만, 위의 식만으로 State-Of-The-Art를 차지할 정도의 혁신적인 결과가 나오지는 못했습니다. 그래서 연구진은 Positional Encoding과 Hierarchical Sampling 과정을 통해서 더 NeRF를 Optimize했고 그 결과 SOTA quality를 가진 결과물을 낼 수 있게 됩니다.
1. Positional encoding
NeRF의 경우는 저차원의 input을 갖고 있기에, high resolution의 image를 도출하는데 불리함이 있습니다. 그렇기에 연구진은 input을 higher dimensional space에 mapping함으로써 이러한 문제를 해결하였습니다. 위에서 언급했던 에 대해서 로 표현을 하면서 performance를 확장해주었습니다. 여기서 는 을 로 mapping 해주는 parameter로 다음과 같은 식으로 표현이 됩니다.
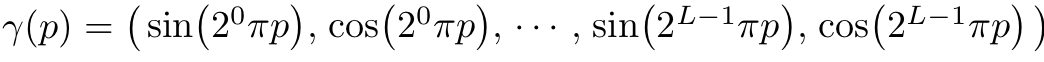
는 에 속해있는 3 좌표에 대해서 따로 분해되서 사용되며 이러한 과정은 와도 동일하게 나타나며 L의 값은 사용자가 설정하는 값으로 본 논문에서는 에 대해서는 으로,에 대해서는 로 설정하였다고 합니다.
Positional encoding에 대한 mapping은 Transformer에서 사용한 positional encoding과 비슷한 성격을 띄고 있지만, 이 두 Positional encoding은 목적부분에서 차이가 있다고 합니다. Transformer의 경우는 model에게 token들의 순서에 대한 정보를 알려주기 위함이지만 NeRF의 경우에는 MLP로 하여금 더 고밀도 함수를 처리할수 있도록 input coordinate를 고차원의 공간으로 mapping하는 방법이라고 합니다. 아래 사진은 위에서 언급하는 view dependent 기법과 positional encoding 기법을 적용했을 경우와 적용하지 않았을 경우에 대한 비교 사진이다.

2. Hierarchical volume sampling
연구진이 사용한 N개로 ray로 분할 후 값을 얻어내는 rendering 기법은 free space와 occluded된 부분은 결과값에 별 기여를 안하기 때문에 비효율적이라는 단점을 갖고 있습니다. 그렇기에 scene을 표현하기 위해 단 하나의 network를 사용하기보다는 coarse network와 fine network로 구분해 두 가지 network를 학습시키는 방법으로 network를 진행시켰습니다. 위에서 설명한 방법으로 진행된 network는 coarse network에 가까우며, 주어진 coarse network의 결과에 따라 fine network의 구성이 바뀌게 됩니다. coarse network에 대해서는 우선 다음과 같이 다시 표현할 수 있게 됩니다.
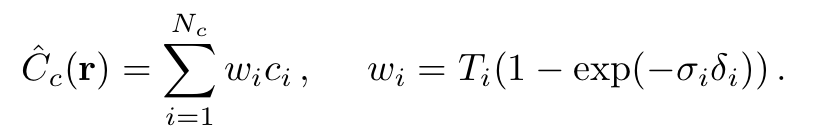
해당 식에 대해서 값들 Normalizing해주면 값들에 대한 하나의 PDF가 형성이 되고 이러한 PDF를 기반으로 값이 높은 곳에 대해서 , Fine하게 더 세세한 색의 분포를 얻게 됩니다. 즉 개의 색 분포를 얻게 되는 결과를 얻으며 이를 기반으로 한 최종 Loss function은 다음과 같습니다.
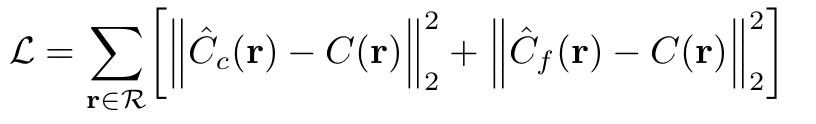
Result
수치적으로는 다음과 같은 결과를 얻었다고 합니다.

사진을 기반으로 한 비교를 보면 다음과 같습니다.

좀 더 세부적인 구현 결과에 대한 내용은 다음 링크에서 확인할 수 있습니다. 보면 굉장히 신기합니다...
https://www.matthewtancik.com/nerf
Reference
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis - Ben Mildenhall, Pratul P. Srinivasan
