A Survey of Trustworthy Graph Learning: Reliability, Explainability, and Privacy Protection

1. Introduction

• DGL의 다양한 활용 분야: finance (e.g., fraud detection, credit modeling), e-commerce (e.g., recommendation system), drug discovery, advanced material discovery
  $\rightarrow$ 하지만 GNN의 trustworthiness가 문제가 됨
• 오늘날, various emerging laws and regulations in AI ethics, e.g., EU GDPR, promote different companies to develop trustworthy algorithms for meeing regulatory compliance requirements of privacy, explainability and fairness, etc.
• DGL (Deep Graph Learning): Accuracy
  $\downarrow$
  TwGL (Trustworthy Graph Learning): Accuracy, Reliability, Explainability, Privacy Protection

2. Reliability

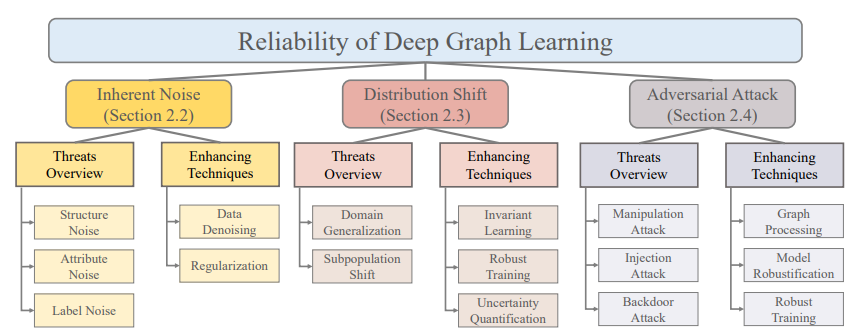
• 정의: 다양한 potential threats (Inherent noise, Distribution shift, Adversarial attack)에도 robust 해야함

• Potential threats 구분
  

• Summary - Reliable DGL
  

• Reliablity against Inherent Noise

  • Threats Overview
    • Structure Noise
      • 생기는 원인: error-prone data measurement & collection, sub-optimal graph construction with task-irrelevant edges
      • 왜 악영향을 끼치는가?: DGL은 message-passing scheme에 기반하고 있기 때문
    • Attribute Noise
      • 생기는 원인: raw attribute의 부정확성, information loss when transforming raw node attributes into node embeddings
      • 왜 악영향을 끼치는가?: DGL은 message-passing scheme에 기반하고 있기 때문
    • Label Noise
      • 생기는 원인: unavoidable erroneous annotations
      • 왜 악영향을 끼치는가?: DL 자체가 label noise에 오버피팅 되는 경향이 있기 때문
  • Enhancing Techniques
    • Data Denoising
      • Structure noise의 해소: Task-desired subgraph만 추출하여 사용 (assign learnable weights for each node, self-attention module 도입, prune task-irrelevant edges)
      • Label noise의 해소: Graph 구조를 도입하건 하지 않건간에 수행하는 label correction (backward loss label correction, random walks 기반 label aggregation, pseudo labels 기반 high-quality edges 생성)
      • Attribute noise의 해소: 특별한 방법이 아직 개발되지 않음, 특히 앞선 세가지 noise를 동시에 제거할 수 있는 방법이 개발되면 좋을 듯함
    • Regularization
      • 핵심: Reduce overfitting to inherent noises by decreasing the complexity of the gypothesis space implicitly or explicitly
      • Implicit regularization: randomly drop edges, nodes, or hidden representations of GNNs, Bayesian graph learning framework, advanced augmentation (Mixup) 기반 ensemble
      • Explicit regularization: building GNN models with some predefined constrains or inductive bias (p-Laplacian based GNNs)

• Reliablity against Distribution Shift

  • Threats Overview
    • Domain Generalization
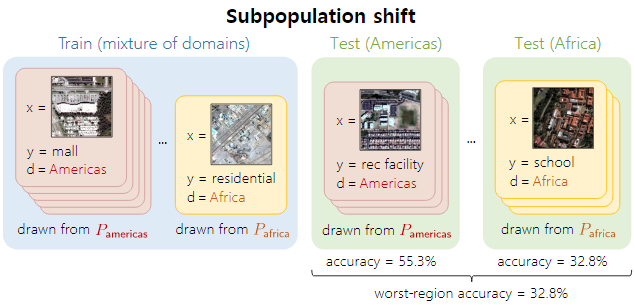
      Training and testing distributions consist of distinct domains (e.g., covariate shift, open-set recognition)
      
    • Subpopulation Shift
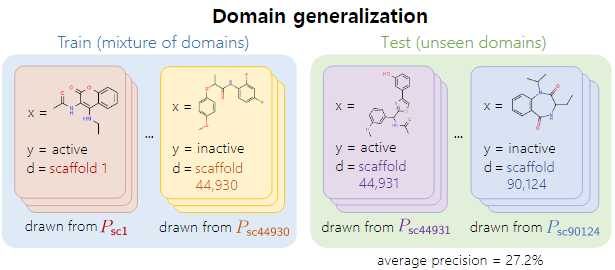
      Training and testing distributions consist of the same group of domains but differ in the frequencies of each domain (e.g., fairness, label shift a.k.a. class-imbalance)
      
  • Enhancing Techniques
    • Invariant Learning
      • 핵심: learn invariant graph representations across different domains that well extrapolate between the training and testing domains
    • Robust Training
      • 핵심: Enhance the model robustness against distribution shift either by data augmentation or modifying the training framework
      • Data augmentation: Mixup, fairness-aware data augmentation
      • Integrate adversarial training technique: Iteratively augments node features with adversarial perturbations during training and helps the model generalize to out-of-distribution samples by making it invariant to small fluctuations in input data
    • Uncertainty Quantification
      • 핵심: 위 두 방식이 model robustness를 키우는 것이라면, 이 방식은 rejecting unreliable decisions with high model predictive uncertainties와 같이 쓰임
      • Introduce probabilistic blocks into original GNNs (Softmax layer $\rightarrow$ Gaussian process block) 왜냐면 GNNs with Softmax prediction layer are typically under-confident 하기 때문
      • Bayesian GNNs: transforms whole GNN layers into Bayesian counterparts
      • Confidence calibration by temperature scaling (성능 $\downarrow$)

• Reliability against Adversarial Attack
  Recent studies have shown that GNNs are vulnerable to adversarial attacks, posing significant security risks to several application domains. Therefore, the adversarial reliability of GNNs is highly desired for many real-world systems, especially in security-critical fields.

  • Threats Overview
    Adversarial attacks can be performed in the training phase (poisoning attack) and the inference phase (evasion attack)
    • Manipulation Attack (training, inference)
      Graph structure 혹은 node attributes를 수정하여 adversarial sample을 만듦 (일반적으로 supervised signal에 기반하여 만들지만, unsupervised adv attack에서는 graph contrastive loss를 기반으로 만들 수도 있음)
      • GF-Attack (black-box)
    • Injection Attack (training, inference)
      The manipulation attack requires the attacker to have a high privilege to modify the original graph, which is impractical for many real-world scenarios. Alternatively, injection attack has recently emerged as a more practical way that injects a few malicious nodes into the graph.
      • Poisoning attack setting: reinforcement learning based framework to poison the graph (malicious node를 빼는데도 RL-based approach를 쓸 수 없을까?)
      • Evasion attack setting: 효과적으로 공격하기 위해서는 inject할 노드의 attribute와 structure을 동시에 고려해야함
      • 관측: the success of injection attacks is built upon the severe damage to the homophily of the original graph $\rightarrow$ optimize a harmonious adversarial objective to preserve the homophily of graphs
    • Backdoor Attack (training)
      Node 혹은 (sub)graph 형태를 띠는 backdoor trigger을 사용하여 backdoor trigger이 포함된 input은 공격자가 원하는 target label로 분류하도록 만듦
      • A work selected the optimal trigger for GNNs based on explainability approaches.
  • Enhancing Techniques
    • Graph Processing (data 관점)
      • Process the training/testing graph to remove adversarial noise thus mitigating its negative effects
      • Currently supported by empirical observations on specific adversarial attacks
      • 장점: cheap implementation cost, adversarial robustness $\uparrow$
      • 단점: difficult to resist unseen attacks, trade-off between performance and robustness
    • Model Robustification (model 관점)
      • The robustification of GNNs can be achieved by improving the model architecture or aggregation scheme.
        • Employ different regularizations or constraints on the model itself
        • Robust median function instead of mean function to improve the aggregation scheme
    • Robust Training(optimization 관점)
      • Adversarial training
        • Make adversarial samples via specific perturbations on the graph structure, node attributes, and even hidden representations
        • 단점: adversarial samples에 오버피팅, evasion attack에만 robust함
      • Enhance the model robustness against poisoning attacks through transferring knowledge from similar graph domains.
        • GCN-LFR

• Overall Discussion

  • For the message-passing based models used by most DGL algorithms, the adversarial perturbation, inherent noise and distribution shift of one node can be transmitted to its neighbors and further hinder the model performance.
  • One can inject probabilistic decision module into GNNs to provide predictions and its uncertainty estimation. Uncertainty estimation can be further enhanced by introducing OOD and adversarial samples into the training phase. Thus, the estimation can be used to detect the above threats, improving the decision reliability of various DGL algorithms.

• Future Directions

  • 현실에서는 세가지 threats가 동시다발적으로 일어날 수 잇으므로, unified solution 개발 필요
  • From the optimization perspective, how to build robust learning algorithm for DGL is an interesting direction (there is a strong connection between robustness and learning stability)
  • 실세계의 large-scale 그래프에 위 메소드들을 적용하는 연구가 필요
  • Explore fair and robust DGL algorithms and develop principled evaluation metrics beyond accuracy
  • In vision tasks, counterfactual explanations and adversarial samples are shown to be strongly related approaches with many similarities[94] $\rightarrow$ 확장 to DGL

3. Explainability

• GNNs are generally treated as black-box since their decisions are less understood, leading to the increasing concerns about the explainability of GNNs
  $\rightarrow$ It is imperative to develop the explanation techniques for the improved transparency of GNNs

• Summary - Explainability of GNNs
  

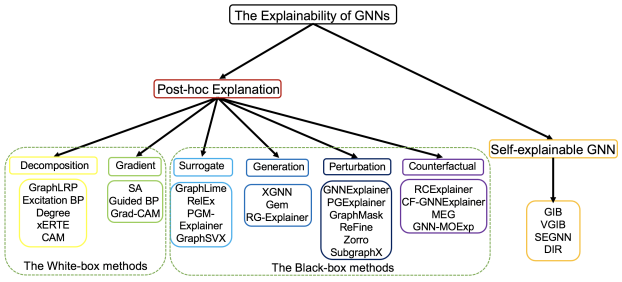
  • Post-hoc Explanation
    Highlight the important patterns of the input graphs such as nodes, edges, and sub-graphs which are crucial for the model predictions
    • White-box: 모델 파라미터 및 gradient에 접근 가능
    • Black-box: 모델의 input과 output에만 접근 가능
  • Self-explainable GNN
    Make predictions and produce the corresponding explanations simultaneously, need built-in module for intrinsic explanations (도메인 지식 기반)

• Post-hoc White-box Methods

  • Decomposition-based
    Decompose the prediction into the contributions of different input substurctures
    • GraphLRP: ML의 해석 메소드인 LRP(Layer-wise Relevance Propagation)을 GNN에 적용한 것임 $\rightarrow$ compute the node-level importance scores of the final preictions in terms of the weights and the hidden representations of the GNN layers (relevance $\ne$ gradient)
      
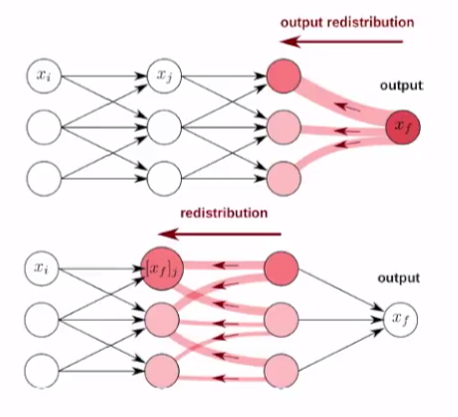
    • Excitation BP: GraphLRP와 비슷하게 LRP를 도입하지만 bayesian perspective을 추가
    • DEGREE: two-stage method; first decomposes the contributions of the node groups, and then generates subgraph-level explanation via the aggregation algorithm (more human-intelligible than the node-level explanation)
    • xERTE: iteratively sample the relevant edges and nodes that are important to forecast future links in the temporal knowledge graph, interpretation+improved performance
    • CAM: identifies the important node features by decomposing the contributions of the node features in the last graph convolutional layer instead of the input domain, only applicable to the GNN model with GAP layer, only applicable for graph-level tasks
  • Gradient-based
    Employ the output-gradient or logits-gradient w.r.t. the input graph to identify the importance of the input portions
    • SA: the higher gradient norm(square norm of the gradients w.r.t. node features and edge features), the higher influence on the prediction $\rightarrow$ node-level, feature-level explanation
    • Guided-BP: SA에서 negative gradients를 clipping하여 발전시킴
    • Grad-CAM: CAM과 비슷하지만, employs the gradients instead of weights between the GAP and the FC layer(CAM의 아이디어) to sum up different feature contributions, GAP layer 없는 GNN에도 적용 가능하지만 여전히 graph-level tasks에만 applicable

• Post-hoc Black-box Methods

  • Surrogate
    Leverage a simple and explainable model to fit the output space of the complex graph model
    • GraphLIME: XAI의 LIME 메소드를 그래프에 확장한 것으로, 인풋 노드와 k-hop 떨어진 이웃 노드의 feature들, 그리고 node class prediction을 가지고 HSIC Lasso 등의 surrogate 모델을 fit함. Model-agnostic한 메소드지만 node classification task에만 적용 가능함
    • RelEx: 어찌보면 surrogate와 perturbation-based 방식의 중간에 있는 것 같은데, 여기서는 surrogate으로 GraphLIME처럼 가벼운 interpretable 모델을 쓰기 보다는 원래 graph model을 쓰되 로컬 데이터셋을 전체 그래프의 k-hop subgraph으로 구성후 원래 graph model과 surrogate 간의 disagreement를 줄임으로써 중요한 node feature을 파악함, 이 메소드도 node-level tasks에만 applicable
    • PGM-Explainer: 여기서는 surrogate으로 explainable Bayesian network를 사용하며, 로컬 데이터셋은 k-hop subgraph의 랜덤한 node feature에 perturbation을 가한 그래프로 구성함, 이 메소드는 node-level, graph-level tasks에서 모두 사용 가능
    • GraphSVX: 인풋 그래프에 node masks와 feature masks를 가함으로써 perturbed samples를 만들고, surrogate으로 interpretable Weighted Linear Regression(WLR) 모델을 사용함으로써 노드와 노드 feature의 importance를 구함, 이 메소드는 node, graph classification에서 모두 사용될 수 있음
  • Generation-based
    Use generative models to synthesize the crucial patterns customized for an input, or generate key structures to globally explain the behavior of model predictions
    • XGNN: 각 인풋 instance 별로 커스터마이징 된 explanation을 제공하기 보다는 특정 class에 전반적으로 적용될 수 있는 essential 그래프 패턴을 만듦, RL을 활용하여 graph generator로 하여금 reward를 높일 수 있는 edge를 점차 부착하게 만들며, policy gradient를 optimizing 함으로써 학습됨
    • RG-Explainer: 또한 RL을 활용하여 GNN의 예측에 대한 explanation을 생성하는데, policy 학습 목표는 input prediction과 subgraph의 label distribution 사이의 mutual information을 최대화 하는 것임. 이 메소드는 node-level, graph-level tasks에 모두 쓰일 수 있음
    • GEM: GNN explanation을 causal 학습으로 보고, input instance에 대한 prediction의 causal subgraph를 생성 후 그 사이를 graph auto-encoder로 mapping함, 이 메소드는 model-agnostic하며, node-level, graph-level tasks에 모두 활용 가능
  • Perturbation-based
    Remove the unimportant edges and nodes so that the final prediction remains unchanged under such perturbations
    • GNNExplainer: 뭔가 읽기에는 RG-Explainer과 비슷하게 느껴짐. Trainable parameter로써 soft mask를 랜덤 초기화 한 후, 원래 adjacency matrix와 element-wise multiplication 함으로써 perturbed 그래프를 만듦. Mask는 원본 그래프와 perturbed 그래프의 prediction 사이 mutual information을 최대화 하는 방향으로 optimize됨. 각 그래프 instance에 대해 각기 다른 mask가 만들어지고 적합되므로 local explanation을 제공할 수 있음
    • PGExplainer: 모두 동일한 방식의 메소드이고, 유일한 차이는 무엇을 mask로 두냐, 어떻게 perturbed graph를 만드냐의 차이이기 때문에 이에 대해서만 언급하겠음. 여기서는 edge mask를 쓰고 제거될 edge의 분포가 베르누이 분포를 따르게끔 최적화 됨. 이 때 Gumbel-Softmax가 쓰여 end-to-end 학습이 가능. 데이터셋 내의 다양한 그래프 instances에 대해 edge predictor이 학습되므로 global explanation을 제공한다고 말할 수 있음
    • GraphMask: PGExplainer과 거의 동일한데, 두 가지 차이점은 첫째, masking할 edge가 정해지면 drop하는 것이 아닌 baseline으로 대체한다는 점과 둘째, straight-through Gumbel-Softmax를 써서 strictly discrete mask를 쓴다는 점임. 역시나 global explanation을 제공함
    • ReFine: 앞의 세 모델이 각각 local 혹은 global explanation 중 하나만을 제공할 수 있었다면, ReFine은 둘 다, 즉 multi-grained explanation을 제공할 수 있음. 2-stages 중 pre-training 단계에서는 predictor을 여러 그래프에 대해 학습시키고, finetuning 단계에서 specific instance에 대해 적합시키기 때문에 이가 가능한 것으로 보이지만, 실제 작동 원리와 이유가 unclear함
    • Zorro: 이 친구는 greedy algorithm을 통해 하나씩 input nodes와 node features을 perturb 해보며 가장 높은 fidelity score를 갖는 노드를 선택함으로써 해석을 제공해줄 수 있는 subgraph를 만들어나감. 이 메소드는 local explanation을 제공함
    • SubgraphX: 이전 방법들처럼 mask를 학습하고 이런건 아니고, Monte Carlo Tree Search(MCTS) 알고리즘을 통해 다양한 subgraph 중 가장 중요한 subgraph를 선정함. 이 때 reward로는 Shapley value를 사용함. Shapely value를 사용하여 가장 human-intelligible한 local explanation을 제공하지만, MCTS 특성상 연산량이 어마무시함
  • Counterfactual-based
    Identify the minimal substructure of the input which would change the original prediction if removed
    * Counterfactual Explanation(반사실적 설명): X가 발생하지 않았다면 Y가 발생하지 않았을 것, 반사실적 설명은 예측값을 사전 정의된 결과값으로 변경하는 특성값의 작은 변화를 설명함
    • CF-GNNExplainer: Iteratively removes edges from the adjacency matrix based on matrix sparsification techniques until the prediction of the input changes. Counterfactual subgraph가 반드시 원 prediction의 원인이 되는 것은 아니므로 faithfulness의 문제가 있음
    • RCExplainer: Counterfactual explanation이 input noise에 더 강건하도록 만듦 $\leftarrow$ GNN의 decision logic을 linear-wise decision boundary로 모델링 함으로써. 이전 방식에 비해 faithfulness가 개선됨
    • MEG: 얘는 특별히 molecule property prediction task에서 counterfactual explanation을 만들어 내는 친구이며, RL을 활용하여 substructure을 정제해 나간다는 특징이 있음
    • GNN-MOExp: 사람의 인지 과정을 따라하는 2-stage, multi-objective 방법인데, 일단 explanation의 simulatability를 평가 후, 괜찮다 싶으면 두번째 stage로 넘어가서 counterfactual relevance를 평가받게 됨. 이 메소드는 타 메소드들에 비해 더 comprehensive, human-intelligible한 explanation을 도출할 수 있음

• Self-explainable Methods
  Embed the intrinsic explanations in the architectures of the GNN models so that they can make predictions and generate the corresponding explanations during the infrerence time, simultaneously. Either recognize the predictive substructures of the input graph or induce the evidence of the outputs via regularization. (학습 프레임워크 자체를 바꾸는 느낌인 것 같음)

  • GIB: Information Bottleneck 기술을 그래프 학습에도 확장 적용하여 Graph Information Bottleneck 프레임워크를 제안함. 인풋 그래프가 들어오면 compressed yet informative subgraph인 IB-Subgraph를 만들고, 이 IB-Subgraph만을 GNN의 인풋으로 이용하여 compression term과 prediction term을 동시에 최적화 함. 이 IB-Subgraph가 원본 그래프의 explanation으로 사용될 수 있음
  • VGIB: GIB의 unstable training을 gprah perturbation+subgraph selection으로 바꿈으로써 단번에 해결함. 이 메소드는 node-level, graph-level tasks에 모두 적용 가능함
  • DIR: 확실히 이해는 안가지만 causal inference를 사용했음은 알 수 있음
  • SEGNN: 그냥 단순하고 heuristic한 방법으로 node classification task에서 K-Nearest Neighborhood clustering을 통해 노드 라벨을 결정하는 방식임

• Datasets and Tools (for explainability!!!)

  • The evaluations of graph explanation are non-trivial because annotating the ground-truth explanations require intensive labor and even expertise.
  • Synthetic graph datasets: BA-shapes(node classification), BA-Community, Tree-Cycle, Tree-Grids, BA-2Motifs $\rightarrow$ 문제: simple synthesis로 인한 simplistic evaluations
  • Sentiment graph datasets(+with text): Graph-SST2, Graph-SST5, Graph-Twitter
  • Molecular graph datasets: MUTAG, BBBP, Tox21, QED, DRD2, HLM-CLint, RLM-CLint
  • Tools: PYGeometric(https://github.com/pyg-team/pytorch_geometric), DIG(https://github.com/divelab/DIG)

4. Privacy (PPGL; privacy-preserving graph learning)

• Federated Graph Learning (FGL)
  그래프 데이터가 device간에 어떻게 분배되었는지에 따라 4가지 종류로 분류할 수 있음, 내 연구분야가 전혀 아니기 때문에 생략하겠음
• Privacy Inference Attack
  • Membership Inference Attacks (MIA)
    • Aims to determine if a target graph element (e.g., a node or an edge) is within the victim model's training set (data-level attack)
    • test phase에 일어남
      
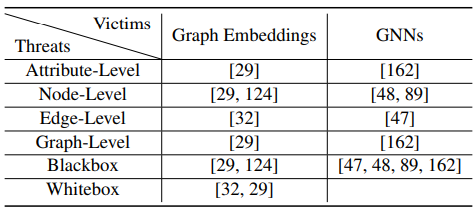
  • Model Extraction Attacks (MEA)
    • Aim to reconstruct a surrogate model with similar performance as the victim model (model-level attack)
    • test phase에 일어남
• Private Graph Learning
  • Differential privacy (DP) based
  • Multi-party computation (MPC) based
    Employ cryptographic techniques to prevent privacy inference attacks

• Counterfactual Explanation - https://moondol-ai.tistory.com/430
• Adversarial Attack - https://blog.lgcns.com/2191