확률분포 | 연속확률분포와 이산확률분포 | 정규분포, 표준정규분포, t분포, 카이제곱분포, f분포, 이항분포

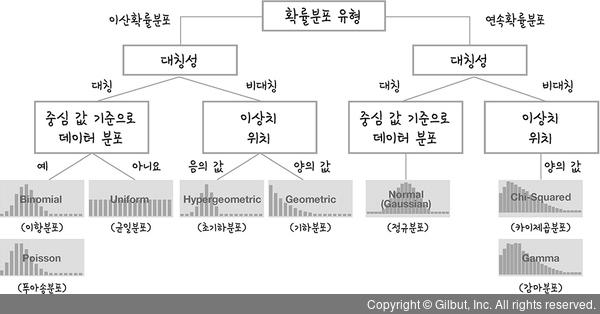
확률분포는 연속확률분포와 이산확률분포로 나뉜다. 확률분포란 확률변수에 대하여 정의된 실수를 0과 1 사이의 실수(확률)에 대응시키는 함수이다.

• 이산확률분포 PMF
• 연속확률분포 PDF
• 누적확률분포 CDF

1. 정규분포
   가우스분포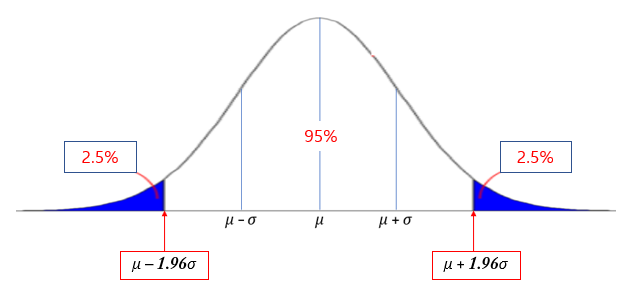
   X ~ N(mu, sigma)
   prob = stats.norm.cdf(x, mu, sigma)

2. 표준정규분포 (z분포)
   정규분포 밀도함수를 통해 X를 Z로 정규화함으로써 평균이 0, 표준편차가 1인 표준정규분포
   z검정에 사용된다.

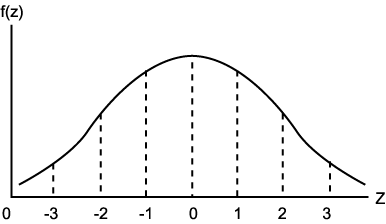
Z ~ N(0, 1)

3. t 분포
   정규분포의 평균을 측정할 때 사용
   표준 정규분포와 유사하게 0을 중심으로 좌우대칭
   표준 정규분포보다 평평하고 기다란 꼬리를 가짐
   모집단의 평균을 추정할때 (모표준편차 모를때) 정규분포 대신 사용
   자유도가 클수록 표준정규분포와 비슷
   회귀분석에서 개별 회귀계수의 유의성 검정

stats.t.cdf(t, df)

4. 카이제곱 분포
   정규분포를 따르는 모집단에서 크기가 n인 표본을 무작위로 반복하여 추출할 때, 각 표본에 대해 구한 표본분산들은 카이제곱 분포를 따름
   모집단의 분산을 추정할 때 사용
   빈도 기반의 분포 또는 형태 적합도 검정
   여러 집단 간의 독립성/동질성 검정

stats.chi2.cdf(chisq, df)

5. f 분포
   분산이 같은 두 정규모집단으로부터 크기 n1과 크기 n2인 확률표본을 반복하여 독립적으로 추출한 후, 구한 두 표본분산의 비율들의 표본분포
   두 분포의 분산을 비교하는 데 사용 (자유도 2개)
   아노바 분석에서 그룹 내 변동과 그룹 간 변동 여러개의 평균값 비교할 때 사용
   회귀분석에서 회귀모형 자체의 유의성 검정

stats.f.cdf(f, dfn, dfd)

6. 이항분포
   베르누이 실험을 여러번 실행해서 특정한 횟수의 성공/실패 또는 양품/불량품이 나타날 확률을 알고자 할 때
   확률밀도함수 P(X=x) = Cp(1-p)
   기대값 E(X) = np
   분산 V(X) = np(1-p)

stats.binom.pmf(k=x, n, p)