Causality and happens-before

Lamport diagram (spacetime diagram)

When we draw events that happen in two processes, we don't know what event causes one another in what time. The diaram like the following seems benign but it definitely causes some confusion.

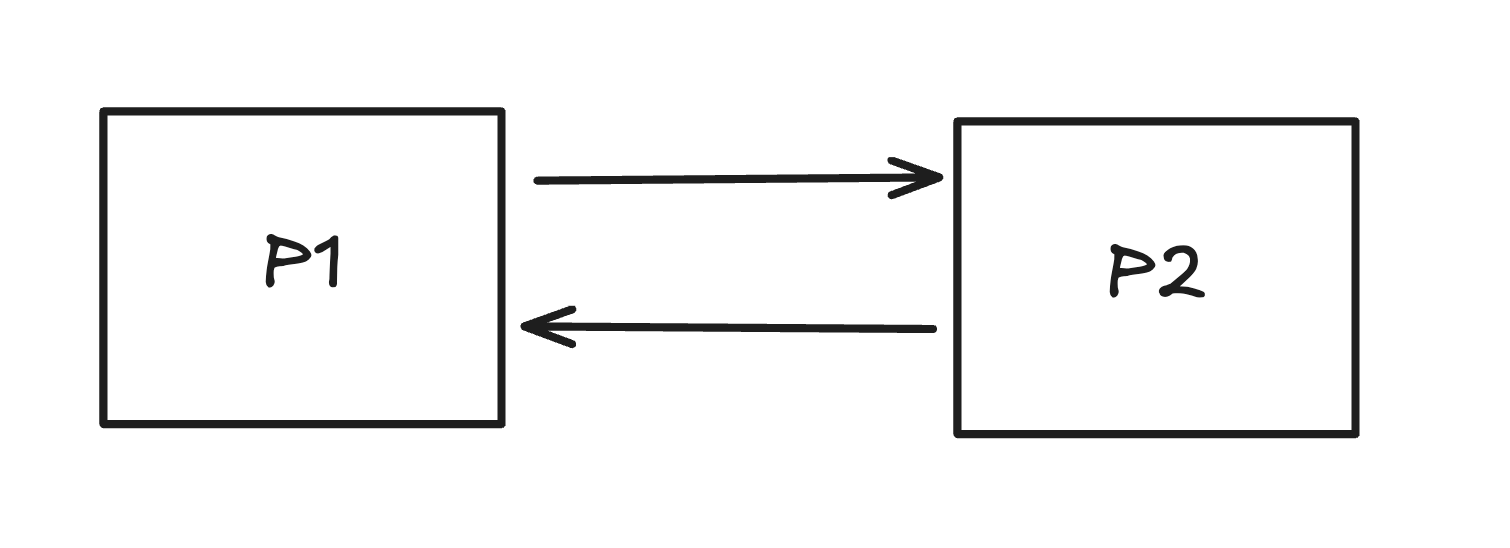
So Leslie Lamport suggested the following diagram instead:

Here, for P1 raises events x, y, z in order, meaning that x might have causes event y, or perhaps it didn't.

Communication between process

Communication between process is also depicted as events as follows

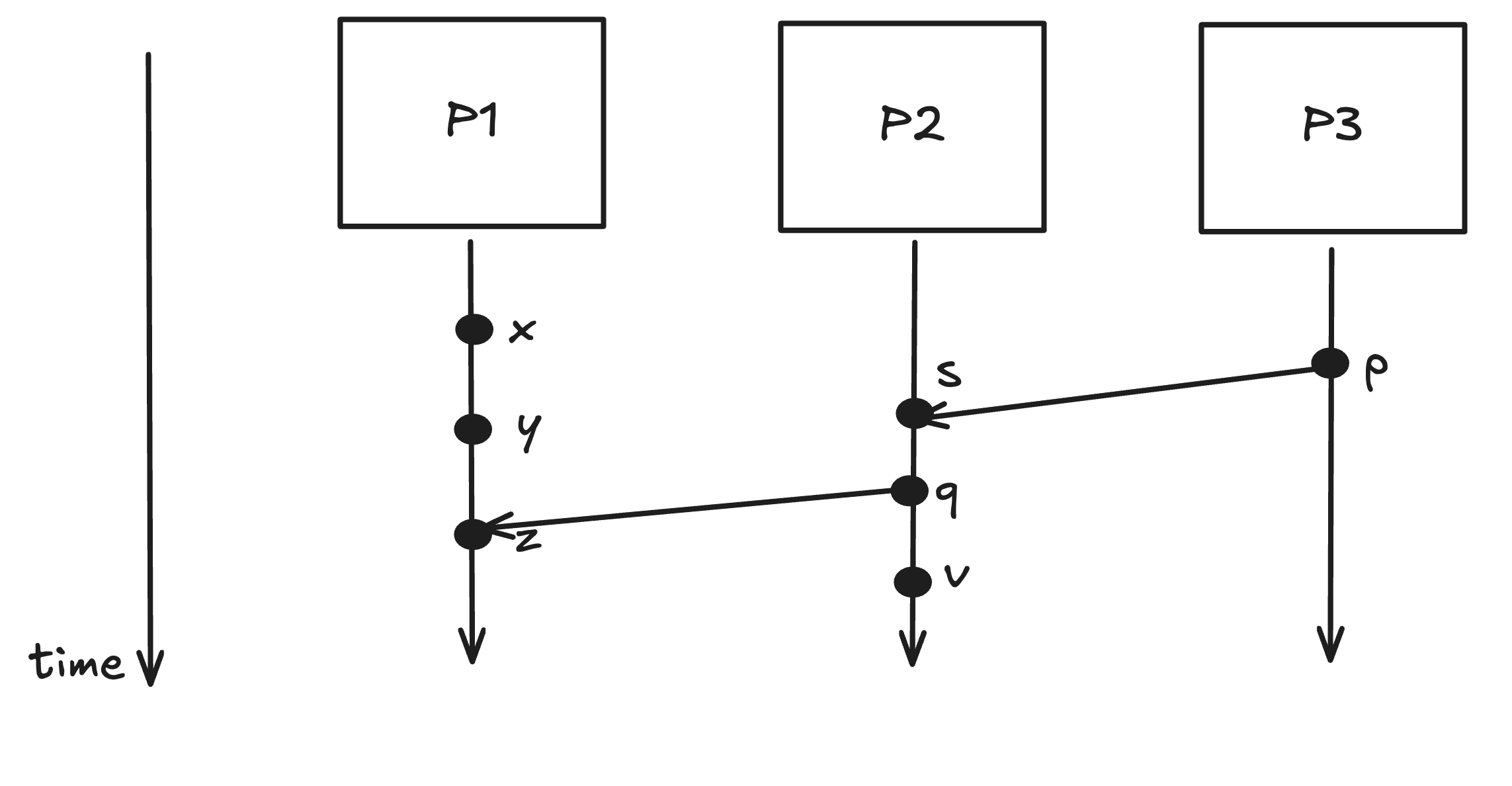
Here, s is probably "message received" event, so is z whereas p and q are "message sent" kind of event. And x, y, v are internal events.

Definition of happens-before

Given two events A and B, we say A happened before B if any of the following is true:

• A and B occur on the same process line with B after A
• A is a message send event and B is the corresponding receive.
• if A->C, and C->B, then A->B (transitive closure)

Causal anormaly

Let's say we have three people in the chat room: Migo, Kay and Carl. Imagine the following situation.

1) Kay sends message saying "Migo is stinky"
2) Migo receives and replies saying "Fuxx you"

But then how do we make sure, from Carl's perspective Kay's message receives arrives first and then Migo's one?

Turns out, there is no guarantee in distributed system unless you have some mechanism.

So, the following could happen.

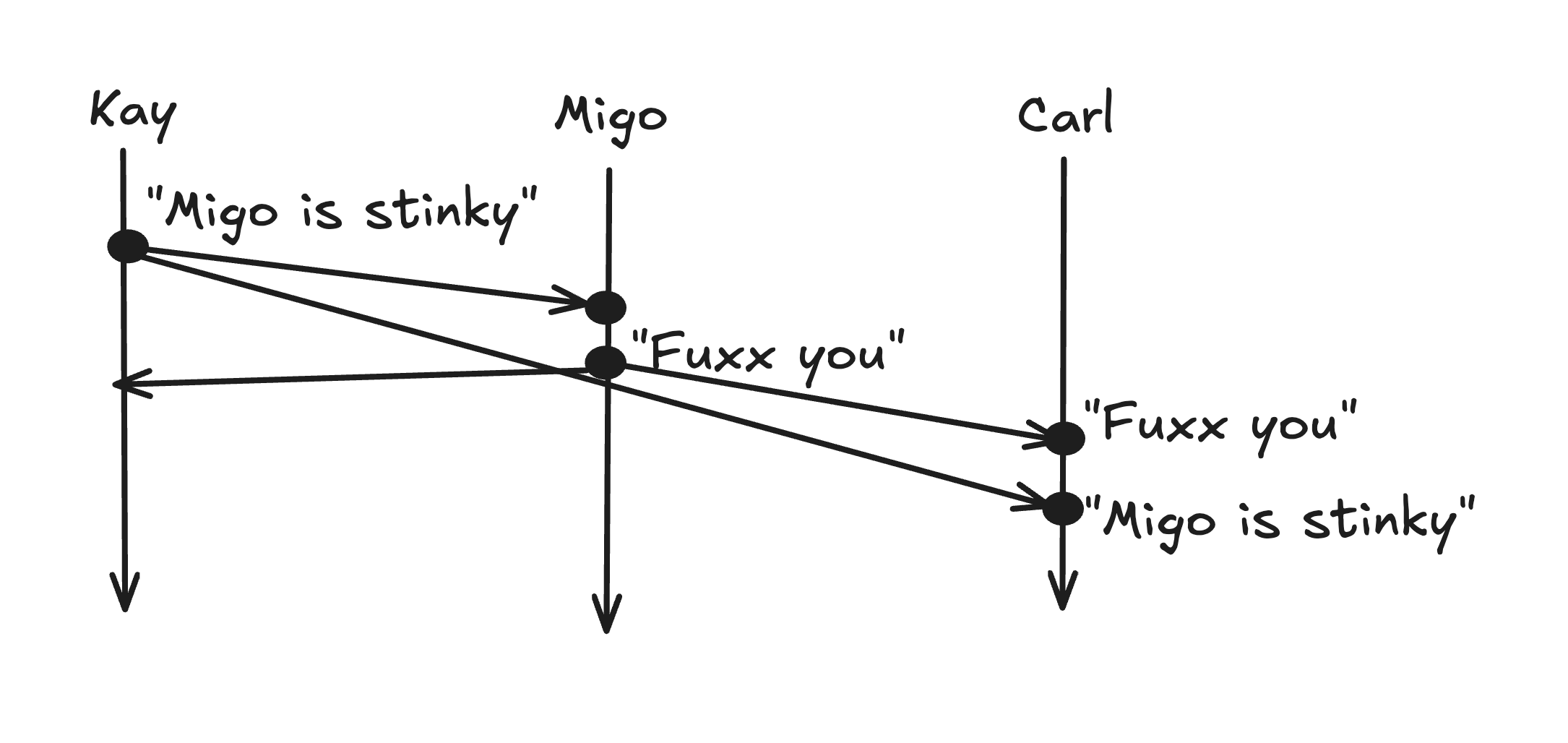
This phenomenon is known as Causal anormaly.

Smallest relation

Happens-before relation is the smallest relation. What it means is it CANNOT confirm if A happens before D from the following:

We know:

• A happens before B (A -> B)
• B happens before C (B -> C)
• A happens before C (A -> C)
• D happens before C (D -> C)

Concurrent

Let's find happens before relationship from the following:

There are happens-before relationships for the following events

• P->S
• X->Z
• P->Z
• U->R
• Z->R

And the like.

But what about Q and R?
We cannot tell is Q happens before R and nor can we say R happens before Q.

When this is the case, we say they are concurrent, also denoted as Q||R.

Partial orders

Happens-before relation is also called Irreflexive Partial Orders - or irreflexive version of partial orders in math.

Partial orders are two things glued together.

• a set S

• a binary relation, usually (but not always) written <=, that lets you compare things from S and has theses properties:

  • Reflexity: for all A that are in set S, A is less than or equal to A

  • Anti-symmetry: for all A and B that are in set S, if A<=B AND B<=A, then A=B

  • Transitivity: for all A,B,C that are in set S, if A<=B and B<=C then A<=C.

Think of set of events mentioned above like (Q,S,X,Z) as the set S in the partial order.

We can check Transitivity, Antisymmetry are right there but Reflexivity is not because for that to be true, it would need to be the case that given an event A, A happens before A.