Logical clocks(1) - Lamport clocks

In the previous post, we discussed why we shouldn't use physical clock in distributed system.

In this post, I'll be talking about number of logical clocks we can use.

Lamport Clocks

Again, Leslie Lamport, the guru and father of distributed system.

Let's say we have event A and LC(A)=3 denotes that:

• If A->B, then LC(A) <= LC(B)

Lamport clocks are consistent with causality. This means that if there's a causal relationship between A and B then we know that LC(A) is less than or equal to LC(B)

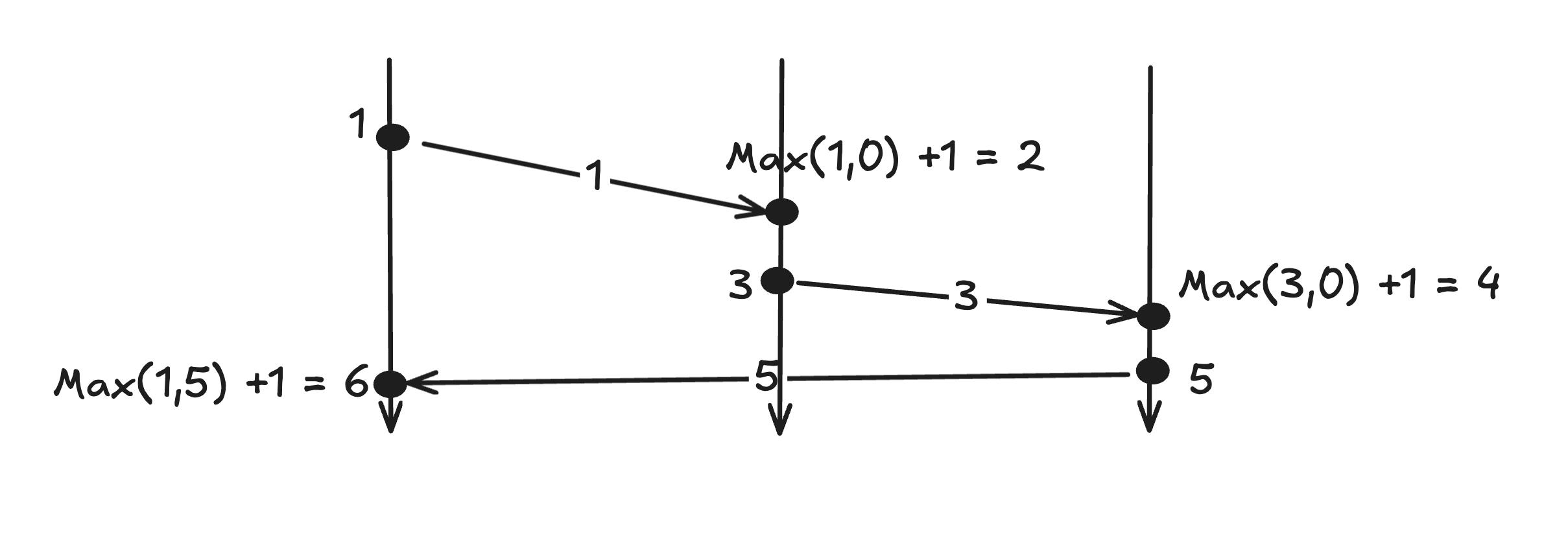
Given the following diagram, let's assign the lamport clocks to events.

Here is the rule:

• Every process has a counter initialized with zero.
• On every event, a process increments its counter by one.
• When sending a message, a process includes its current counter along with the message.
• When receiving a message, set your counter to max(local counter, message counter) plus one.

Note however in some formulation of this algorithm, "message received" is not counted as events. For now, let's consider that as event.

The following is the result:

Now, we know that if A happens before B, then LC(A) < LC(B) for sure. But is the following also true?

If LC(A) < LC(B), then A happens before B?

Perhaps surprisingly the answer is NO.

Let's look at an example and try to give lamport clock numbers to the event:

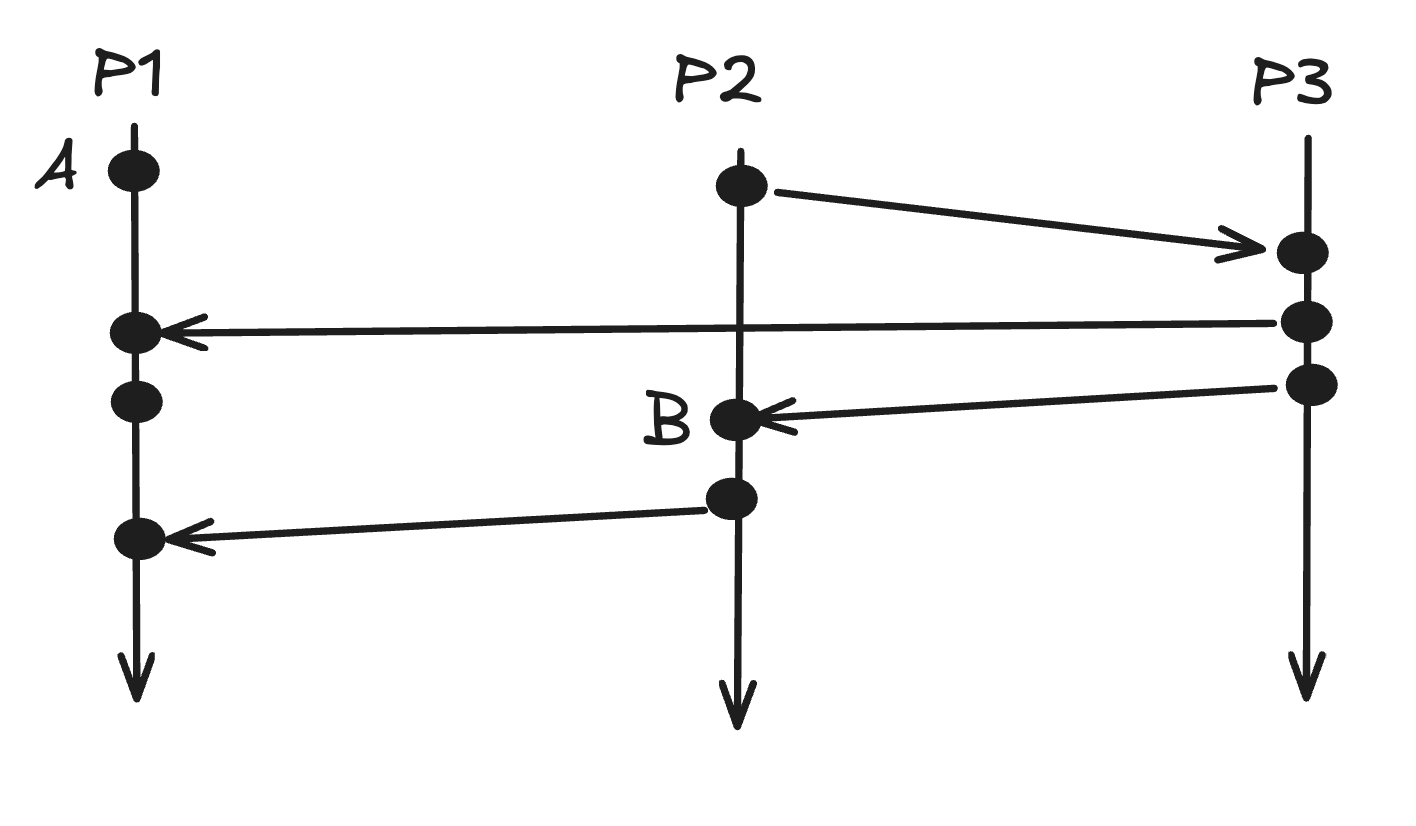
When you give the lamport clock to each event according to the rules above, it is as follows:

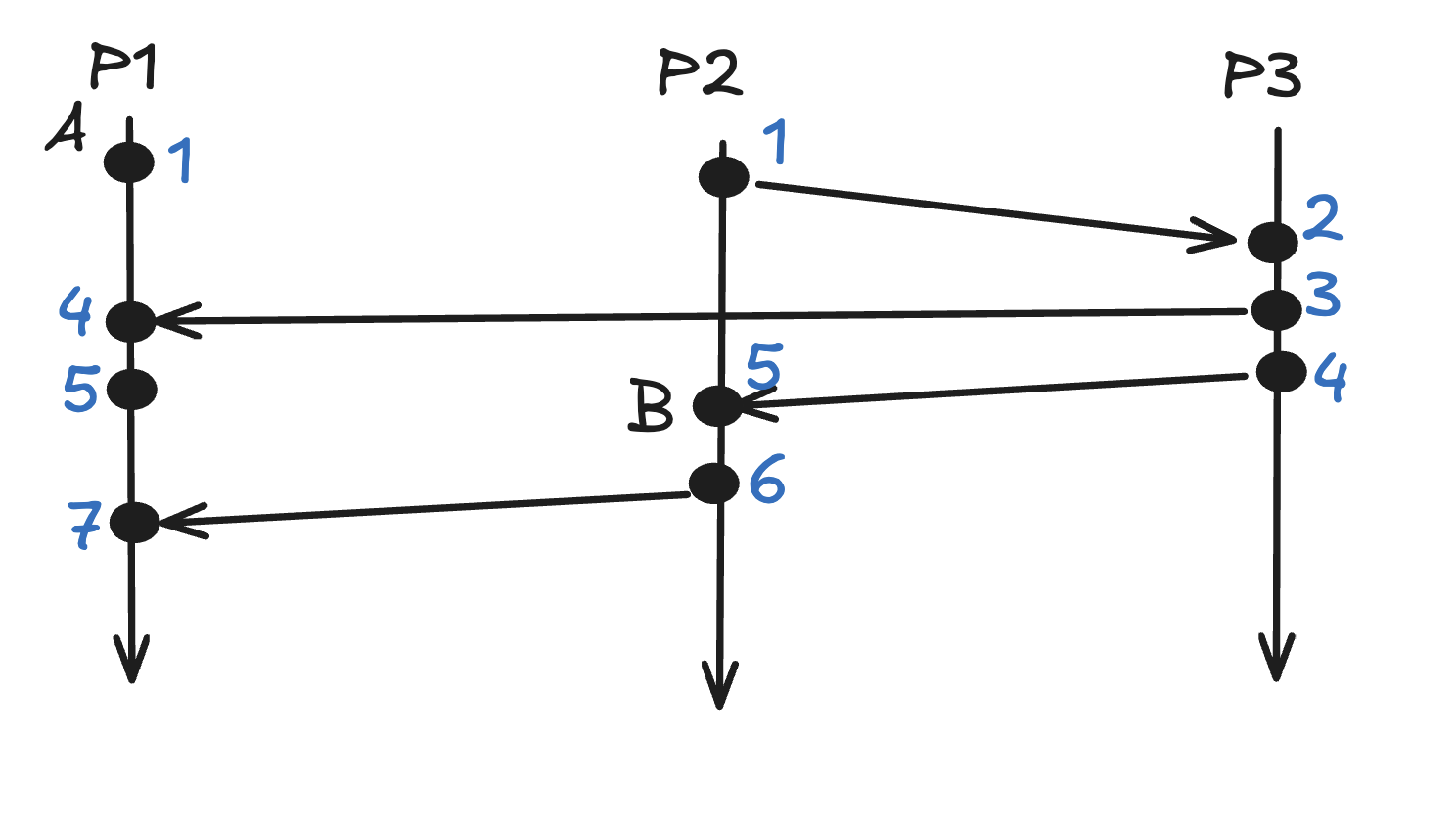
Here is the question: Does A happen before B?

The first way for one event to happen before another is when they're on the same process line - which they don't.

Or, one has to be a send and the other has to be a corresponding receive - which they don't.

Or, they have to be happens before relationship by transitivity - that's not the case either.

So, now we have situation where the Lamport clock of A is less than Lamport clock of B but it certainly doesn't mean that A happened before B.

Now we confirm the following statement:

Causality is graph reachability in spacetime

Which is very fancy of saying that "You try to follow the graph from A to B, if you can reach B, they are causally related.

So as you can see, Lamport clocks are consistent with causality because if A->B then LC(A) < LC(B).

But it's not the case that if LC(A) < LC(B) then A->B, meaning that Lamport clocks do not characterize causality.

Use case for Lamport Clock

So, should we throw away Lamport clock and move on to the next? Well, even though it doesn't characterize causality, it has its own goodness because it's still true that if A->B then LC(A) < LC(B)

We can conclude the following counter positive of the statement.

if !(LC(A) < LC(B)) then !(A ->B)

With this, we can rule out things as not having caused other things. When debugging, this will be a useful technique.

But still, it is, with all due respect to the foundational work, kind of a week tool to be used - we want something better, and there comes Vector clocks, suggested by Schwarz & Mattern - which will give us the other half of implication