활성화 함수의 이해(FUN23)

(1) 활성화 함수(activation function)

• 활성화(activated) or 비활성화(deactivated) = 조건을 만족 or 조건 불만족

• 신경망 속의 퍼셉트론(혹은 노드) 도 특정조건이 만족하면 활성화가 되도록 디자인되어 있음

• 노드에 입력으로 들어오는 값이 어떤 임계치를 넘어가면 활성화가 되고, 넘어가지 않으면 비활성화가 되게끔 코딩이 되어있음

  • 예로 ReLU 함수 : 입력값 음수(0미만) 조건 만족 0출력, 0이상이면 입력값 그대로 출력

• 활성화 혹은 비활성화 표현하려면, 활성화되는 기준이 먼저 정해져야함

  • 예로 출력값이 0보다 큰 경우를 활성화 되었다고 정의한다면, ReLU 함수란 0미만일때는 비활성화가 되고 0이상인 경우에 활성화가 되는 함수가 된다고 할수있다.

• 시그모이드

  • −∞ 로 갈수록 0을 출력하고 +∞ 로 갈수록 1을 출력하며, 0일 때는 1/2 을 출력하는 함수
  • 입력값에 '무관하게' 0∼1 사이의 값으로 출력하는 특징이 있으며, 따라서 "참" / "거짓" 혹은 "앞면" / "뒷면" 처럼 2가지 상황을 구분할 때 용이(참=0, 거짓=1 로 대응 시켜 구분)

@ 활성화 함수를 쓰는 결정적 이유!!!!

• 딥러닝 모델의 표현력을 향상시켜주기 위해서
• 모델의 representation capacity 또는 expressivity를 향상시킨다라고 함
  • 선형" 함수(직선)로는 "비선형"함수(사인곡선 혹은 고차항)을 표현할 수 없다
  • 딥러닝 모델의 파라미터(f(x)= Wx+b 에서 W 와 b를 가리킴)들은 입력과 x와 선형관계임, 곱하고 더하는 연산만 하면서 그다음 레이어로 전달 하는데 이런것들이 아무리 겹쳐도 결과는 선형이 된다.
  • 사인곡선처럼 직선으로는 근사시킬수없는(고양이,강아지사진처럼 무수히 많고 복잡한 특징을 가진) 비선형 데이터를 표현하려면 딥러닝 모델도 비선형을 지니고 있어야함
  • 이때 쓰인것이 '활성화 함수'
  • 활성화 함수를 레이어 사이 사이에 넣어줌 -> 모델이 비선형 데이터도 표현할수 있게 되었음
  • 활성화 함수 : 하이퍼볼릭 탄젠트, 시그모이드, 소프트맥스, 렐루 등이있다.

(2) 퍼셉트론

• 우리가 알고있는 딥러닝 모델은 보통 여러개의 층으로 이루어져있음

• 그 한 층을 가져와 다시 쪼개면 '노드'라고 불리는 것으로 쪼개짐

• 쪼개진 노드를 퍼셉트론이라고 함

• 퍼셉트론을 쌓으면 단층 퍼셉트론, 이 단층퍼셉트론을 쌓으면 다층 퍼셉트론이 됨

• 결국 딥러닝 모델은 퍼셉트론들이 다양한 구조로 쌓인것

• 퍼셉트론은 어떻게 나온것일까?

  • 우리의 목표는 컴퓨터를 학습시키는 것
  • 학습시키는 방법은 잘 자인 머신이라고할수잇는 동물의 학습방법을 모방하기로함
  • 학습방법을 모방하기 위한 학습시킬 머신자체를 동물의 신경세포와 유사하게 설계해 나오게 된것이 최초의 퍼셉트론!

(2-1) 신경세포의 구조

• 신경세포(Nueron)
• 신경세포의 구성
  • 세포체(몸) : 각 가지돌기로부터 들어온 신호드롤부터 자신의 출력신호를 만들어 다음 세포에 전송, 출력신호는 비선형방식으로 결정, 합이 일정수준이하이면 비활성상태로 무시, 일정수준을 넘으면 활성상태가 되어 신호를 다음 세포로 전송
  • 가지돌기(머리) : 세포로 전달되는 신호를 받아들이는 부분
  • 축삭돌기(발) : 세포에서 다른 세포로 신호를 전달하는 부분
  • 시냅스 : 가지돌기와 축삭돌기 사이에 있는 부분, 신호전달의 세기 담당, 발달정도에 따라 같은 신호도 강하게 전달되거나 약하게 전달됨, 사용빈도에 따라 커지거나 작아지며 자체가 사라지기도함
  • 한 신경세포의 축삭돌기와 그다음 신경세포의 가지돌기는 연결되어 있고, 그 연결되어 있는 부분에 존재하는 것이 시냅스

(2-2) 퍼셉트론의 구조

• 입력 : 신경세포에서 가지돌기로 받아들이는 신호
• 각 입력항에 곱해지는 가중치: 신경세포들의 연결 부위에 형성된 시냅스의 발달 정도,
• wx 값들은 각 가지돌기에서 스냅스를 거쳐서 오는 신호들에 해당되고 세포체(몸)에서 이 신호들이 합쳐짐, 여기에 신경세포에는 없는 편향이라고 불리는 b 신호가 합산에 포함됨.
• wx값들이 합쳐치고거기에 b신호가 합쳐진 신호는 세포체에서 신호를 처리하는 하는 방식과 비슷하게 적절한 활성한 함수 f 를 거쳐서 출력이 결정됨
• 식을 나타내면
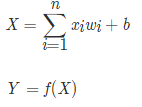
• X는 합쳐진 신호, Y는 퍼셉트론의 최종 출력
• 퍼셉트론을 다양한 구조로 연결, 가중치와 편향값을 적절히 조정해주는것이 신경세포와 유사하게 작동하게끔 만들어줄수있다.
• 적절히 조정하는 과정이 학습이며, 학습을 통해 동물과 비슷한 일(과일분류, 결함 탐지, 음성인식등)을 처리할 수 있게됨

(2-3) 활성화 함수

• 세포체(몸,f)에서 일어나는 일을 맡고있다.
• 들어온 신호가 특정 임계점을 넘으면 출력, 넘지못하면 무시
• 활성화 함수는 신호를 전달하기때문에 Transfer function라고 함
• 활성호 함수의 표현에 따라 두가지로 나눔
  • 선형 활성화 함수(Linear activation function)
  • 비선형 활성화 함수(Non-linear activation function)
    -딥러닝에서는 일반적으로 비선형 활성화 함수를 사용.
    선형 활성화 함수를 딥러닝에서 사용하지 않는 이유는 무엇일까?

2. 선형과 비선형

(1) 선형(Linear)

• 선형 활성화 함수를 사용한다면, 노드의 개수를 아무리 많이 붙여도 결국 하나의 노드를 사용하는 것과 차이가 없다.
  -선형 활성화 함수를 사용한다면, 모델의 표현력이 떨어지게 됨

(2) 비선형(Non-linear)

• 딥러닝에서 비선형 활성화 함수를 주로 사용하는 이유는 러닝 모델의 표현력을 향상시키기 위해서

(3) 비선형 함수를 쓰는 이유

• 그렇다면..(비선형 함수를 쓴다면?)

3.활성화 함수의 종류(hidden layer 사이에 들어가는 활성화 함수)

(1) 이진 계단 함수

• 초기의 퍼셉트론에서 쓰이던 것

• 이 함수로 들어온 입력이 특정 임계점을 넘으면 1(혹은 True)를 출력하고 그렇지 않을 때는 0을 출력

• 이진 분류 문제에서 꽤 유용
  -이진 계단 함수의 치역(range)은 00,11 (00과 11만 나온다는 뜻)
  -단층 퍼셉트론(single layer perceptrons)라는 초기의 신경망에서 자주 사용
  -선형적으로 구분 가능한(linearly separable) 문제(예를 들면, AND gate 또는 OR gate)를 구현 가능

• 하나의 선으로 구분할 수 있는 문제를 풀 수 있다.

• 단층 퍼셉트론은 이 XOR gate를 구현할 수 없

• 이진 계단 함수의 한계

  • 역전파 알고리즘(backpropagation algorithm)을 사용하지 못하는 것
  • 이진 계단 함수는 00에서는 미분이 안 될 뿐더러 00인 부분을 제외하고 미분을 한다고 해도 미분값이 전부 00이 나옵니다. 때문에 역전파에서 가중치들이 업데이트되지않음
  • 현실의 복잡한 문제는 사실상 해결하기 어렵다
  • 다중 출력은 할 수 없다
    • 이진 계단 함수는 출력을 11 또는 00으로 밖에 주지 못하기 때문에 다양한 클래스를 구분해야 하는 문제는 해결할 수 없음

(2) 선형 활성화 함수

• 선형 활성화 함수(linear activation function)은 말 그대로 선형인 활성화 함수
• 다중 출력이 가능, 이진 분류는 물론이고 간단한 다중 분류 문제까지도 해결가능
• 미분이 가능해서 역전파 알고리즘 사용가능
• 대표적인 선형 함수는 f(x)=x, 신호를 받은 그대로 출력
• 선형 활성화 함수의 치역은 실수 전체
• 선형적으로 구분 가능한 문제를 해결가능
• 선형 활성화 함수의 한계는 비선형적 특성을 지닌 데이터를 예측하지 못 한다는 것

(3) 비선형 활성화 함수

• 역전파 알고리즘을 사용가능, 다중 출력도 가능, 비선형적 특성을 지닌 데이터도 예측가능

(3-1) 시그모이드/로지스틱(sigmoid 혹은 로지스틱 logistic)

• 시그모이드 함수의 치역은 (0,1) 즉, 0<<σ(x)<1
• 시그모이드 함수를 쓰는 가장 주된 이유가 바로 치역이 0과 1사이라는 것
• 확률을 예측해야하는 모델에서 자주 사용
• 로그램을 이용해서는 해석 미분을 구할 수 없기 때문에 꽤 많은 분들이 모르는 함수의 미분을 구할 때 수치 미분(numerical differentiation) 을 구한다.
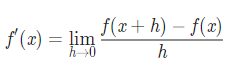
  • 수치 미분: h의 값을 최대한 0에 가까운 값으로 잡아서 실제 미분값에 근사하게 만들어주는 것
  • h의 값을 0에 가까운 아주 작은 수로 잡으면 수치 미분을 통해 계산한 값과 실제 미분을 통해 계산한 값은 차이가 없을 것.적당한 h를 주지 않는다면 생각보다 큰 차이가 있을 수 있음 ((아주 작은 hh를 주려고 h=1e−20이라고 선언한다면, 컴퓨터가 이를 그냥 0으로 인식해 x+h=x라는 결과를 출력)
• 시그모이드 함수 단점
  • 시그모이드 함수는 0 또는 1에서 포화(saturate) : 입력값이 아무리 커져도 함수의 출력은 1에 더 가까워져 갈 뿐 11 이상으로 높아 않고, 입력값이 아무리 작아져도 함수의 출력은 00에 더 가까워져 갈 뿐 00 이하로 떨어지지 않는다 -> 포화가 되면 그래디언트가 0과 아주 가까워지는 것, -> 역전파에서 이 0과 가까워진 그래디언트는 앞에서 온 역전파 값에 곱해지게 되는데 그렇게 되면 그 이후로 전파되는 모든 역전파 값이 0에 근접하게 되어 사실상 가중치 업데이트가 일어나지 않게된다 -> 이것이 그래디언트를 죽인다라고 함(어떤 모델의 초기 가중치 값들을 아주 크게 잡아 포화상태를 만들면 역전파 때 그래디언트가 죽기 때문에 아무리 많이 에포크를 돌려도 훈련이 거의 되지 않음)
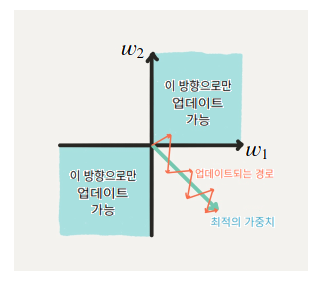
  • 시그모이드 함수의 출력은 0이 중심(zero-centered)이 아님
  • 훈련의 시간이 오래걸리는 것: upstream gradient의 부호에 따라 이 노드의 가중치는 모두 양의 방향으로 업데이트되거나, 모두 음의 방향으로 업데이트가 됨 -> 지그재그로 업데이트(2,4분면방향으로만)되어서, 최적값을 향해 직선적으로 업데이트되는 것보다 훨씬 시간이 오래걸림

(3-2) Softmax

• 10가지, 100가지 class 등 class의 수에 제한 없이 "각 class의 확률"을 구할 때
• 가위, 바위, 보 사진 분류 문제는 3개 class 분류 문제-> softmax는 각 class의 확률값, 즉 (0.2, 0.5, 0.3)(0.2,0.5,0.3) 이렇게 출력값을 준다.
• Softmax는 모델의 마지막 layer에서 활용 : 확률의 성질인 모든 경우의 수(=모든 class)의 확률을 더하면 1이 되는 성질(100%) 때문에

(3-3) 하이퍼볼릭 탄젠트(tanh, Hyperbolic tangent)

• 쌍곡선 함수 중 하나
• 시그모이드 함수의 치역은 (−1,1), 즉, -1<<σ(x)<1
• 하이퍼볼릭 탄젠트 함수를 사용한 모델이 시그모이드 함수를 사용한 모델보다 더 빨리 훈련됨
• 하이퍼볼릭 탄젠트 함수의 단점
  • -1 또는 1에서 포화

(3-4) ReLU(rectified linear unit)

• 최근 가장 많이 사용되고 있는 활성화 함수
• f(x)=max(0,x)
• 치역은 [0,∞]
• 하이퍼볼릭 탄젠트를 사용한 모델보다 몇 배 더 빠르게 훈련됨
• 시그모이드나 하이퍼볼릭 탄젠트처럼 비용이 높은 (예를 들면, exponential와 같은) 연산을 사용하지 않기 때문에 처리 속도가 빠름
• 0을 제외한 구간에서 미분이 가능
• ReLU함수를 사용해도 충분히 x^2와 같은 비선형적 데이터를 예측해낼 수 있다
• ReLU함수의 단점
  • 학습률을 크게 잡게되면 노드가 죽어버림-> ReLU를 사용한 노드가 비활성화 되며 출력을 0으로만 하게되는것, 노드의 출력값과 그래디언트가 0이되는것(노드가죽는것)

(3-5) ReLU의 단점을 극복하기 위한 시도들

• Leaky ReLU
  • ReLU 함수의 'Dying ReLU'를 해결하기 위한 시도 중 하나
  • f(x)=max(0.01x,x)
  • 'Dying ReLU'를 발생시켰던 0을 출력하던 부분을 아주 작은 음수값을 출력하게 만들어 주어 해당 문제를 해결
• PReLU
  • Leaky ReLU와 유사하지만 새로운 파라미터를 추가하여 0 미만일 때의 '기울기'가 훈련되게 함
  • f(x)=max(αx,x)
  • 여기서 α 가 훈련과정에서 업데이트
• ELU
  • ReLU의 모든 장점을 포함
  • 0이 중심점이 아니었던 단점과, 'Dying ReLU'문제를 해결한 활성화 함수
  • 이 함수의 단점은 exponential 연산이 들어가서 계산 비용이 높아졌다