정규화(FUN22)_210811

1. Regularization

• 정칙화
• L1, L2 Regularization( Lasso와 Ridge 모델), Dropout, Batch normalization
• 모델이 train set의 정답을 맞추지 못하도록 오버피팅을 방해(train loss가 증가) 하는 역할
• 오버피팅 : 한국어로 과적합이라고 하며, train set은 매우 잘 맞추지만, validation/test set은 맞추지 못하는 현상
• train loss는 약간 증가하지
• validation loss나 최종적인 test loss를 감소시키려는 목적

2. Normalization

• 정규화
• 데이터의 형태를 좀 더 의미 있게, 혹은 트레이닝에 적합하게 전처리하는 과정
• 데이터를 z-score로 바꾸거나 minmax scaler를 사용하여 0과 1사이의 값으로 분포를 조정하는 것
• 모든 피처의 범위 분포를 동일하게 하여 모델이 풀어야 하는 문제를 좀 더 간단하게 바꾸어 주는 전처리 과정
  • 돈 천원~ 일억사이, 시간 0시~ 24시
  • 학습 초반에는 데이터 거리 간의 측정이 피처 값의 범위 분포 특성에 의해 왜곡되어 학습에 방해를 받게 되는 문제
  • 피처의 스케일이 0과 1 사이로 변환,
  • 가장 큰 값을 1, 가장 작은 값을 0으로 하여 축 범위가 바뀜
  • 데이터의 상대적인 분포는 바뀌지 않음

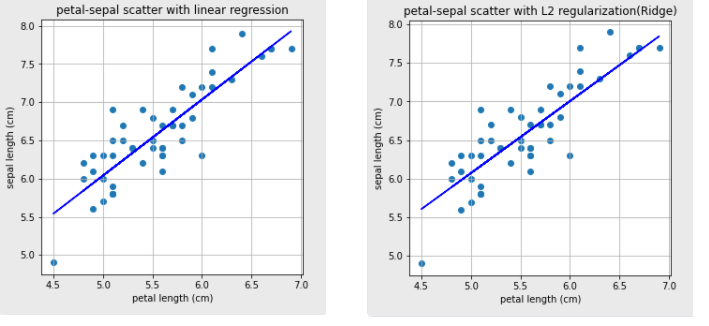
3. Linear regression의 결과값과 L2 Regularization 결과값은 비슷함

4. L1 Regularization

• 가중치가 적은 벡터에 해당하는 계수를 0으로 보내면서 차원 축소와 비슷한 역할
• iris 데이터로 한것
• Linear Regression 문제를 푸는데 L1 Regularization에서는 문제가 풀리지 않음

#L1 regularization은 Lasso로 import 합니다.
from sklearn.linear_model import Lasso

L1 = Lasso()
L1.fit(X.reshape(-1,1), Y)
a, b=L1.coef_, L1.intercept_
print("기울기 : %0.2f, 절편 : %0.2f" %(a,b))

plt.figure(figsize=(5,5))
plt.scatter(X,Y)
plt.plot(X,L1.predict(X.reshape(-1,1)),'-b')
plt.title('petal-sepal scatter with L1 regularization(Lasso)') 
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()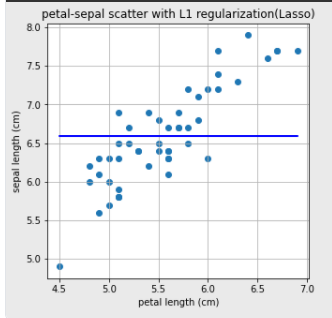

• X가 1차원 값인 선형회귀분석 같은 경우에는 L1 Regularization이 의미가 없다
• L1 Regularization을 사용할 때는 X가 2차원 이상인 여러 컬럼 값이 있는 데이터일 때 실제 효과를 볼 수 있음
• wine dataset(13개의값을 가짐,1행)이용하여 Linear Regression과 L1 Regularization의 차이확인가능(iris 데이터는 특성이 4개로 컬럼수가 너무작아서)
  • print(모델명.coef_)을 통해 확인가능
    • coef_: 기울기(가중치)
  • Linear Regression
    • 모든 컬럼의 가중치를 탐색
  • L1 Regularization
    • 총 13개 중 7개를 제외한 나머지의 값들이 모두 0임을 확인
    • 어떤 컬럼이 결과에 영향을 더 크게 미치는지 확실히 확인가능
• 다른 문제에서도 error의 차이가 크게 나지 않는다면, 차원 축소와 비슷한 개념으로 변수의 값을 7개만 남겨도 충분히 결과를 예측할 수 있다
• Linear Regression과 L1, L2 Regularization의 차이 중 하나는 α라는 하이퍼파라미터(수식에서는 λ)가 하나 더 들어간다는 것이고, 그 값에 따라 error에 영향을 미친다는 점

5. L2 Regularization

• iteration: iteration은 1-epoch를 마치는데 필요한 미니배치 갯수를 의미합니다. 다른 말로, 1-epoch를 마치는데 필요한 파라미터 업데이트 횟수 이기도 합니다. 각 미니 배치 마다 파라미터 업데이터가 한번씩 진행되므로 iteration은 파라미터 업데이트 횟수이자 미니배치 갯수입니다. 예를 들어, 700개의 데이터를 100개씩 7개의 미니배치로 나누었을때, 1-epoch를 위해서는 7-iteration이 필요하며 7번의 파라미터 업데이트가 진행
• 0이 아닌 0에 가깝게 보내지만 제곱 텀이 있기 때문에 L1 Regularization보다는 수렴 속도가 빠르다는 장점

6. norm

• norm : 벡터, 함수, 행렬에 대해서 크기를 구하는 것, 행렬의 Norm
• vector norm
  • p=∞ 인 Infinity norm의 경우는 가장 큰 숫자를 출력
• matrix norm
  • 행렬의 norm
  • p=1인 경우에는 컬럼의 합이 가장 큰 값이 출력되고, p=∞인 경우에는 로우의 합이 가장 큰 값이 출력

7. Dropout

• 확률적으로 랜덤하게 몇 가지의 뉴럴만 선택하여 정보를 전달하는 과정
• 몇 가지의 값들을 모든 뉴런에 전달하는 것이 아닌 확률적으로 버리면서 전달하는 기법
• 오버피팅을 막는 Regularization layer 중 하나
• 확률을 너무 높이면, 제대로 전달되지 않으므로 학습이 잘되지 않고, 확률을 너무 낮추는 경우는 FC(fully connected layer)와 같습니다. fully connected layer에서 오버피팅이 생기는 경우에 주로 Dropout layer를 추가
  • fully connected layer란
    - 완전히 연결 되었다라는 뜻으로,한층의 모든 뉴런이 다음층이 모든 뉴런과 연결된 상태로 2차원의 배열 형태 이미지를 1차원의 평탄화 작업을 통해 이미지를 분류하는데 사용되는 계층입니다.
    1. 2차원 배열 형태의 이미지를 1차원 배열로 평탄화
    2. 활성화 함수(Relu, Leaky Relu, Tanh,등)뉴런을 활성화
    3. 분류기(Softmax) 함수로 분류
    1~3과정을 Fully Connected Layer
    [출처][딥러닝 레이어] FC(Fully Connected Layers)
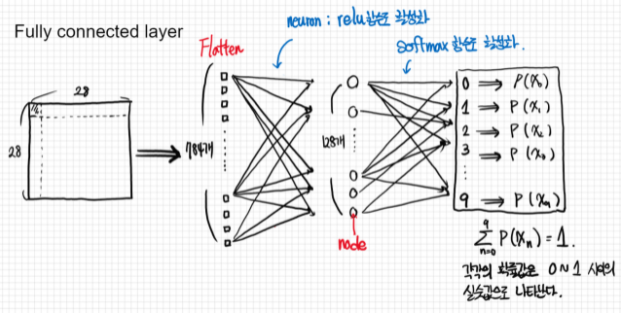    그림출처 : https://dsbook.tistory.com/59
• 코드 : https://keras.io/api/layers/regularization_layers/dropout/
• optimizer='adam' : 옵티마이저란, 머신러닝 학습 프로세스에서 실제로 파라미터를 갱신시키는 부분을 의미,오차역전파법과 같은 방식으로, 각 파라미터의 기울기를 그라디언트로 구하여 재료를 구해왔으면, 이를 이용하여 실제 가중치 변화를 주는 부분

8. Batch Normalization

• gradient vanishing, explode 문제를 해결하는 방법

  • gradient vanishing : 역전파 과정에서 입력층으로 갈 수록 기울기(Gradient)가 점차적으로 작아지는 현상, 입력층에 가까운 층들에서 가중치들이 업데이트가 제대로 되지 않으면 결국 최적의 모델을 찾을 수 없게 됨.
  • explode : 기울기가 점차 커지더니 가중치들이 비정상적으로 큰 값이 되면서 결국 발산되기도 합니다. 이를 기울기 폭주(Gradient Exploding)이라고 하며, 순환 신경망(Recurrent Neural Network, RNN)에서 발생할수있다.
    출처: https://wikidocs.net/21690

• z-score로 normalize

  • Z-점수 정규화,
  • 이상치(outlier) 문제를 피하는 데이터 정규화 전략
  • X라는 값을 Z-점수로 바꿔주는 식 -> (X - mean(평균)) / .std(표준편차)
  • feature의 값이 평균과 일치하면 0으로 정규화
  • 표준편차 : 자료들이 갖는 분포를 확인하기 위한 것이 분산 또는 표준편차, 자료들이 평균 근처에 모여 있는지 아니면 떨어져 있는지를 나타내는 지표, 표준편차의제곱=분산
  • 평균보다 작으면 음수, 평균보다 크면 양수
  • 계산되는 음수와 양수의 크기는 그 feature의 표준편차에 의해 결정
  • 데이터의 표준편차가 크면(값이 넓게 퍼져있으면) 정규화되는 값이 0에 가까워짐

• batch_size=2048

• epoch: 전체 데이터를 1회 훑어 학습하는거

• Step: 파라미터를 1회 업데이트 하는것

• batch_size : step 1회에 사용되는 데이터갯수

예제 참고

• Fashion MNIST 이미지 분류하기https://codetorial.net/tensorflow/fashion_mnist_classification.html
• Iteration * Batch Size = Epoch 이므로, 한 데이터셋을 도는데 최대한 병렬처리가 가능하게끔 배치 크기를 주는게 이득