Point, Line, Edge Detection
이미지에서 점이나 선, 그리고 색과 색깔의 그 경계선을 구분할 때 사용하는 원리를 알아보자.
Digital Derivatives
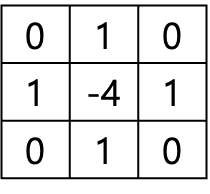
Laplacian(라플라스 연산자)
라플라스는 2계도함수를 나타내는 의미이다.
Gradient
Gradient는 1계도함수를 나타내는 의미이다.
- Magnitude(크기): l-1 norm , l-2 norm
- Phase(방향):
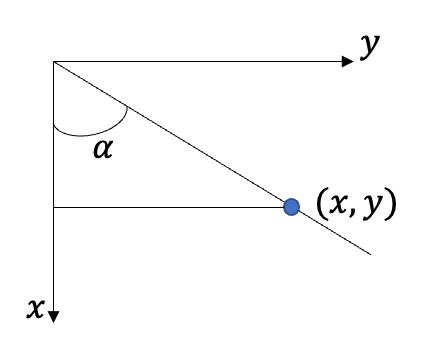
이므로 역함수를 취해 Phase에 대한 식을 구할 수 있다.

순서대로 원본이미지와 x축(세로)의 Gradient, y축(가로)의 Gradient한 이미지이다.
Simple Edge Detection

이미지의 경계선을 추출하는 알고리즘이다.
이전 챕터부터 말한대로, 경계선은 색과 색의 차이가 나는 곳을 뜻한다.
그래서 Gradient를 활용해야한다.
다음의 과정으로 동작한다.
- 이미지를 노이즈를 제거하기위해 smoothing을 한다.
- Gradient를 통해 Intensity 변화율을 찾는다.
- 더 좋은 결과를 위해, Edge후보중 정답을 선택한다. (Threshold)
Principal
Kernel
Central difference를 활용해
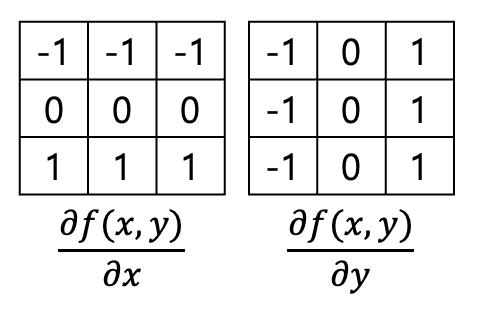
를 더한 방법을 사용한 Prewitt를 사용한다.

결과는 x + y = 전체이므로 제일 오른쪽 이미지처럼 된다.
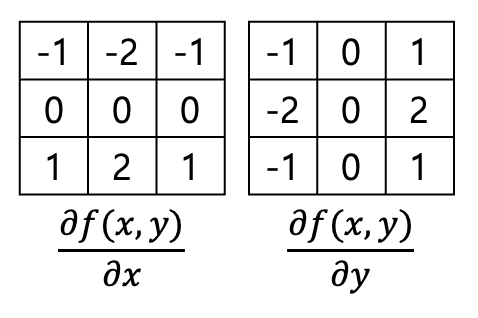
1, 2, 1인 Sobel와 3, 10, 3인 Scharr도 있다.
Threshold
아직 벽의 질감이나 몇몇의 노이즈가 더 존재할 수 있다.
그래서 임계값 를 기준으로 경계를 구분할 필요가 있다.
일정수치이하(노이즈일 수도있고 옅은 신호일 수도 있음)를 없애는 작업을 한다.

Sobel()

Simple Point Detection
점은 사실 아주 작은 픽셀 1개라고 생각하면 Edge Detection보다 쉬워진다.
점은 자신 혼자 Intensity가 크거나, 엄청 작은 값을 뜻한다.
그래서 Sovel이니 Prewitt니 했던 x, y축 방향 상관없이
Principal
Kernel
모든 8방향으로 달라지는 gradient kernel을 만들면 된다.
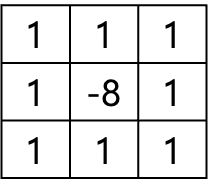
Threshold
마찬가지로 작은 신호(low intensity) 로 잡힌 픽셀은 없애고 그 이상인 데이터는 1로 처리해야한다.
Simple Line Detection
모든 방향으로 밝기 값이 달라지는게 점이라면, Line은 더 간단하다.
Line은 1자로 퍼져나아가기에 Gradient를 다음과 같이 구한다.
Principal
Kernel, Threshold
x축, y축으로 달라지는 gradient kernel을 만든다.
해당 커널을 사용하는 예를 들어보자.
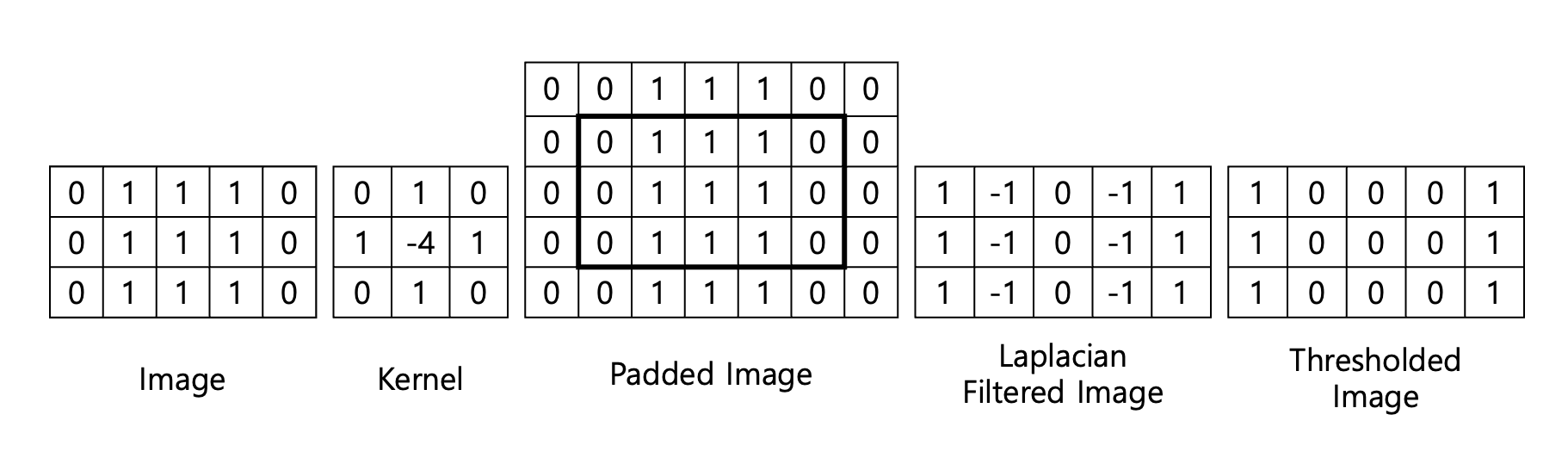
1. Image에서 Convolution을 하기위해 Reflection Padding을 진행
2. Padding을 진행한 이미지와 Kernel을 Convlution하여 Laplacian Filter진행
3. Filtered Image에서 기준으로 Threshold하여 최종이미지 생성
이렇게 되면 기존의 이미지의 테두리를 알 수 있다.
Directional Line Detection
우리는 특정방향의 선을 추출하고 싶을 때도 있을 것이다.
ㅡ 모양으로 평행한 선만 찾고 싶다거나, / 45도 모양의 선을 찾고 싶을 때이다.
이때는 커널을 다음처럼 정해서 만들면 된다.
Principal
Kernel
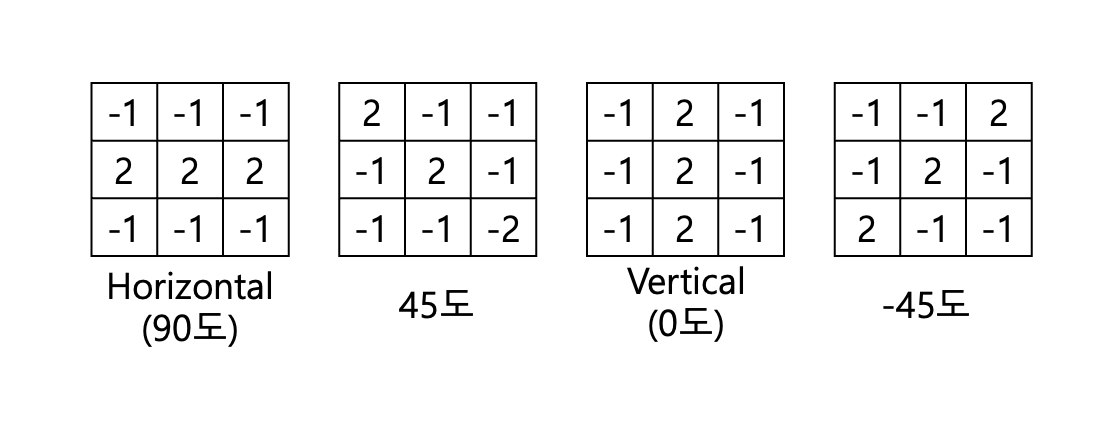
선의 방향과 커널의 모양이다.
를 뒤집은것이라 보면 쉽다.
Horizontal은 ㅡ 모양의 선을 감지하기 때문에 선이 위아래로 밝기가 많이 변하므로 -1, 2, 1이 위아래로 퍼지는 것이다.
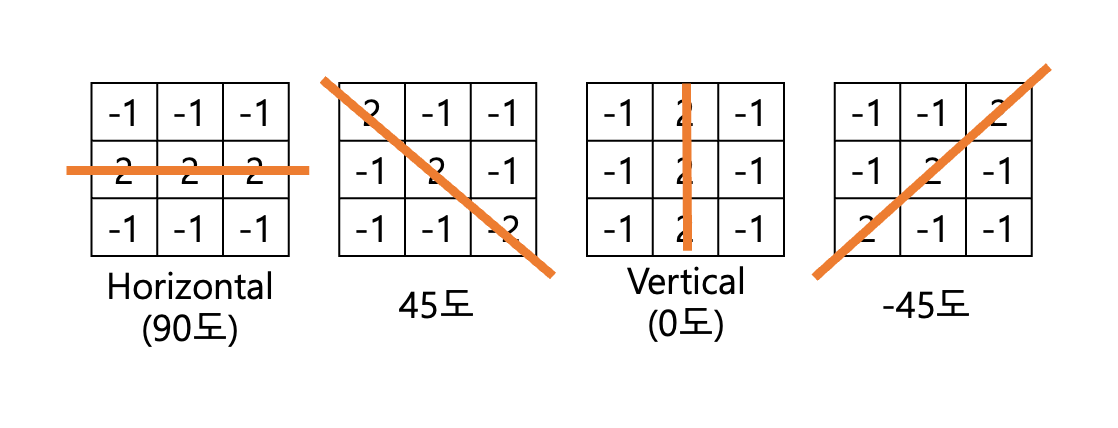
주황색 선이 감지할 선이라고 보면 이해가 빠를 것이다.
Edge Detection
Sovel, Scharr, Prewitt 등의 1계도함수의 원리로 테두리를 검출하는 알고리즘을 배웠다.
계속 봐왔겠지만, 대부분의 영상처리는 해당 Flow로 진행됨을 느낄 것이다.
- 이미지의 노이즈를 제거하기 위해 Lowpass Spatial Filtering을 한다.
- Gradient계산을 하여 이미지의 Intensity 변화 벡터를 이미지로 만든다.
- 필요없는 값을 제거하기 위해 Threshold를 조절하며 최종이미지를 만든다.
이 과정을 응용하여 정확도가 높은 Edge Detection 알고리즘을 공부해볼 것이다.
Marr-Hildreth Edge Detector
Marr-Hildreth 씨는 Lowpass Filter로 Gaussian을 사용한다.
변화량을 뽑기 위해 Laplacian을 사용한다.
하지만 이 두개를 따로 사용하는게 아니라 함수를 하나로 합친다.
이게 우리가 알고 있던 Gaussian Filter라면,
이계도함수를 이용해 를 쓴다.
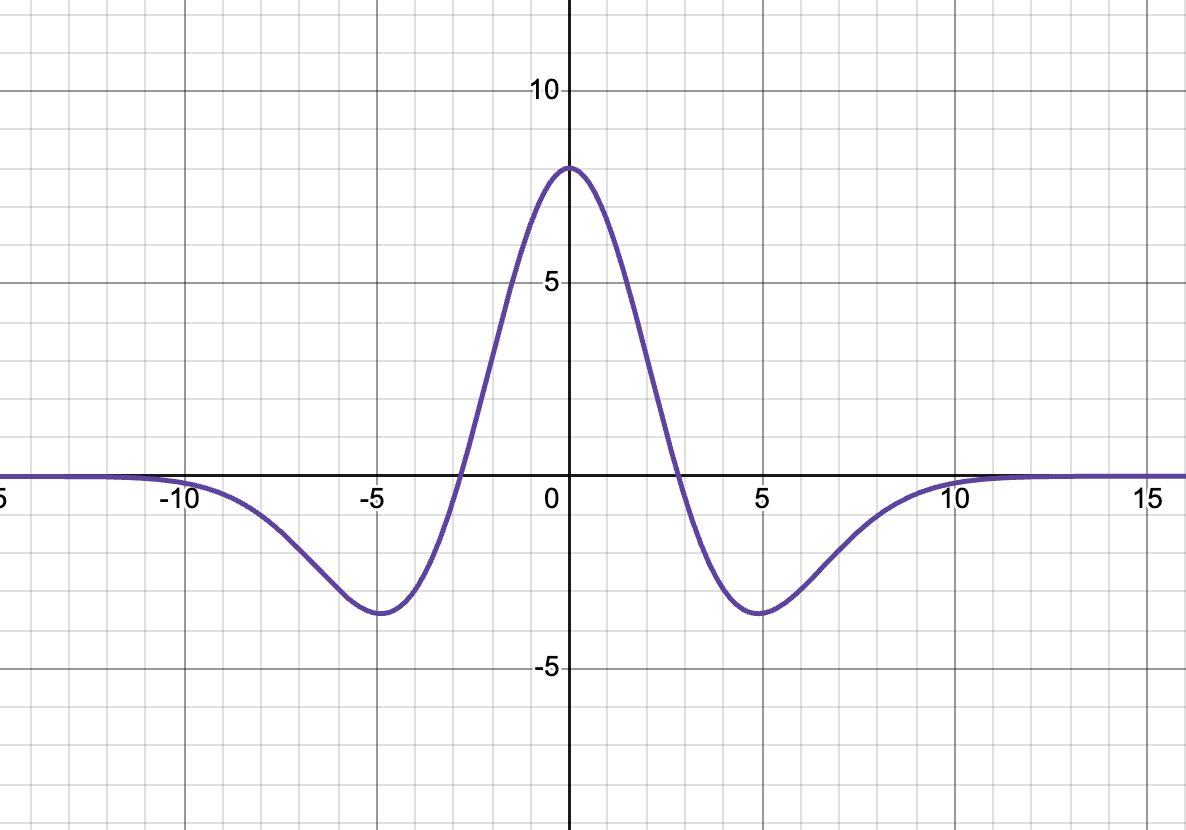
요로코롬 브리또 만드는 아저씨 모자같이 생겼다.
커널은 다음처럼 나타난다.
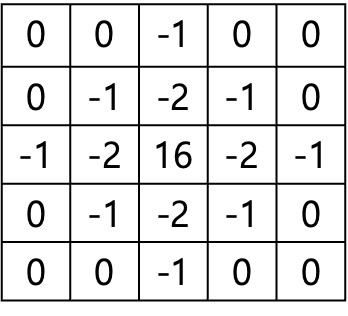
커널에 음수가 들어있기 때문에 실제로 변환된 이미지의 Intensity가 음수인 부분이 생긴다.
양수와 음수가 교차하는 부분이 생기는 Zero Crossing 인 픽셀을 Threshold하여 에지를 검출한다.
Canny Edge Detector
가장 유명한 에지를 검출하는 알고리즘으로 다음의 목적을 가진다.
1. 정확한 검출: 에지가 아닌데 에지로 검출하거나(FP) 에지를 검출못하거나(FN)를 줄이자
2. 정확한 위치: 실제 에지의 중심을 찾자
3. 단일 에지: 하나의 에지는 하나의 점으로 표현하자
Principal
-
노이즈제거를 위해 가우시안 필터를 먹인다.
-
Gradient계산을 위해 x축, y축에 대한 소벨 필터를 먹인다.
위의 phase를 4가지 그룹으로 나눌 수 있다.
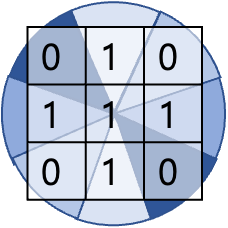
0도, 45도, 90도, 135도 그룹으로 나눌 수 있다.
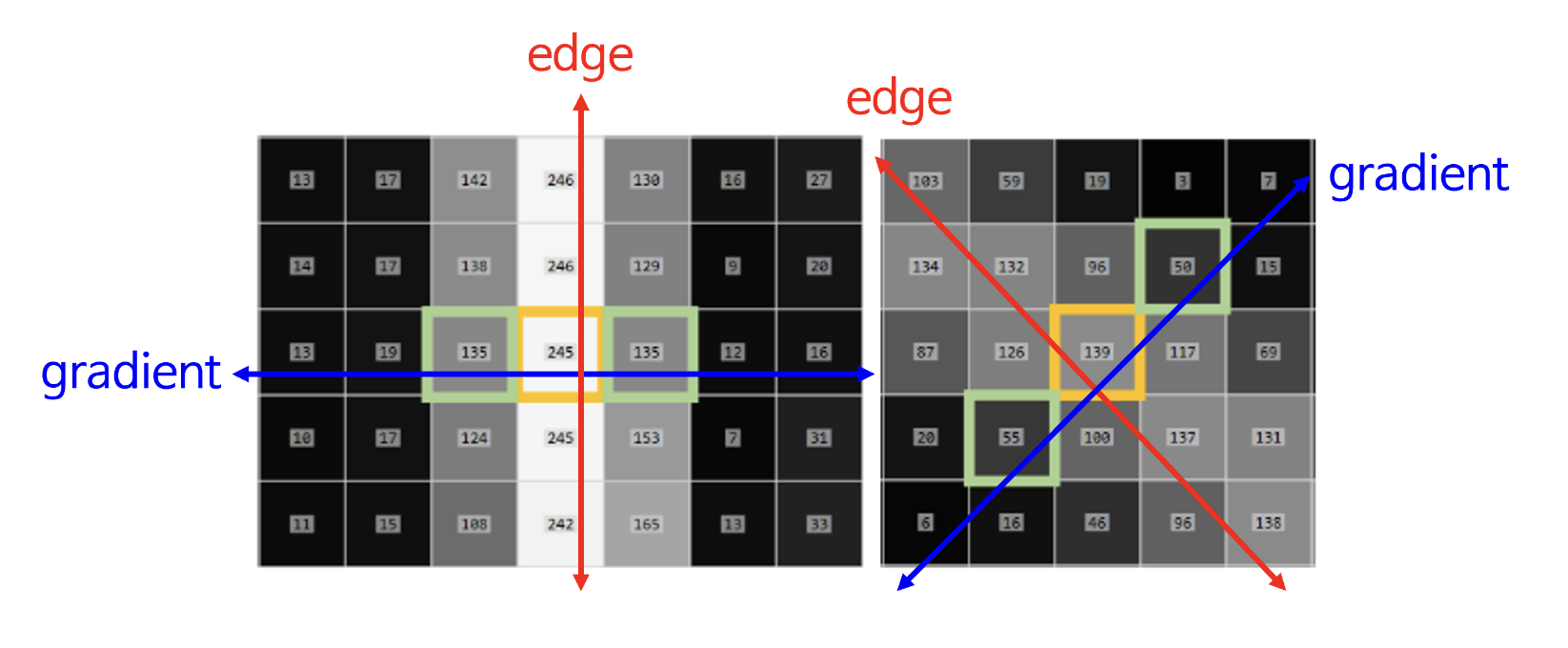
참고로 Edge의 방향은 Gradient방향의 수직이다. -
Non-maximum Suppression으로 에지를 얇게 만든다.
하나의 에지가 여러 픽셀로 두껍게 나타나는 현상을 해결하기 위해 사용한다.
Gradient의 크기가 local maximum보다 큰 것을 Edge로 선정한다. -
Hysteresis Edge Tracking
Double Threshold로 임계값을 두개 선택한다.
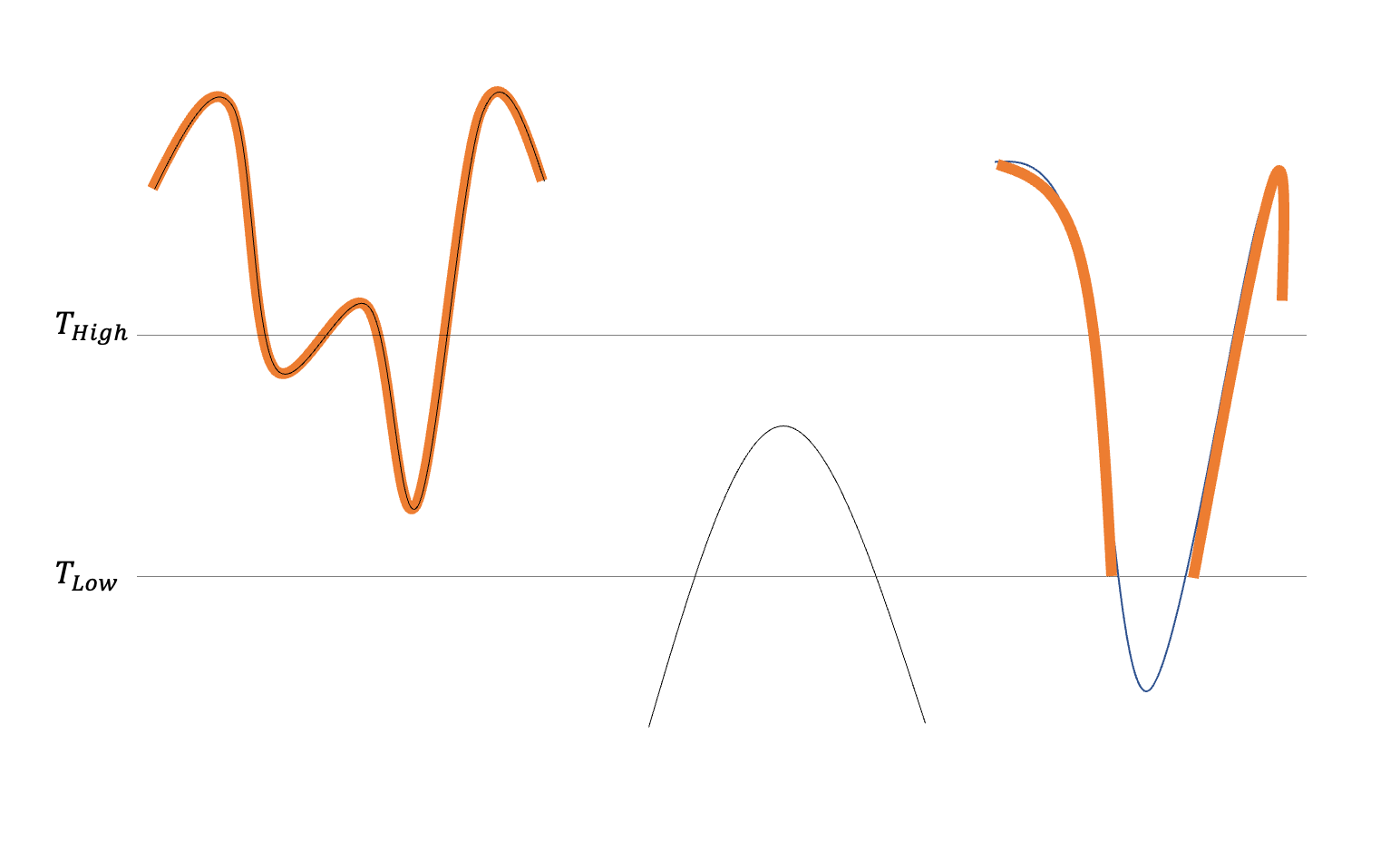
보다 낮은 것은 선택하지 않고, 보다 높은 신호만 있는 것을 선택해야한다.
이렇게 확실한 에지를 검출 할 수 있다.


Hysteresis Edge Tracking을 위한 Threshold를 2개 정해야한다.
Line Detection by Hough Transform
(a, b)를 지나는 선은 로 표현된다. a=1, b=5정도 될것이다.
그리고
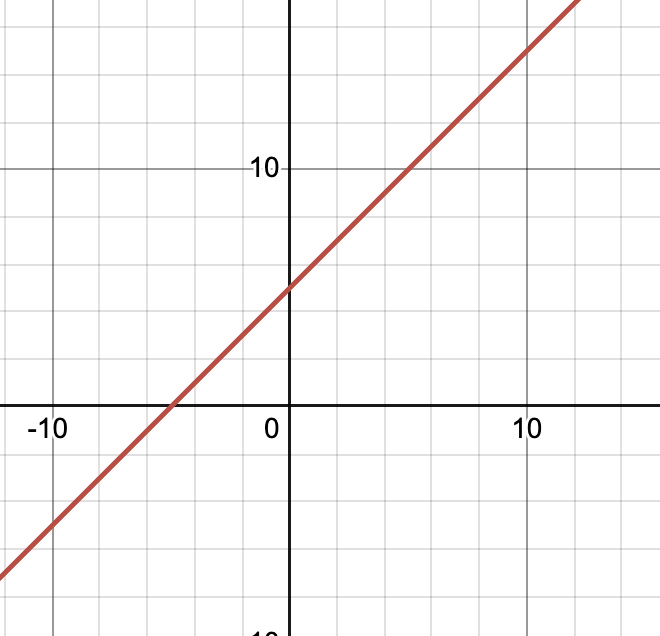
이를 xy 좌표공간이 아닌, ab 좌표공간으로 나타내면?
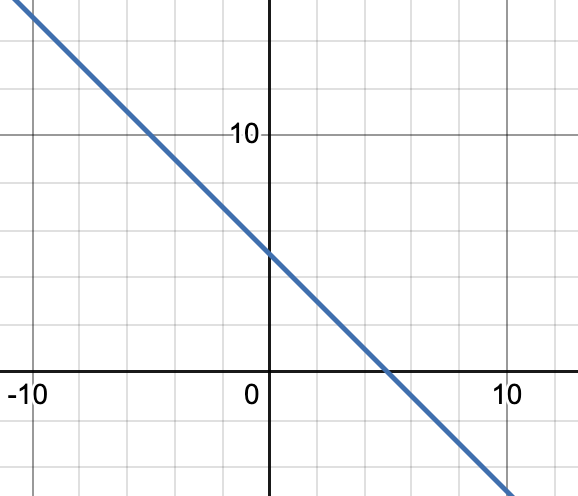
로 표현 될 것이다.
xy공간에서는 (0,5)를 지났던 직선이 ab공간에서는 기울기가 -x고, b절편이 y인 직선이 된다.
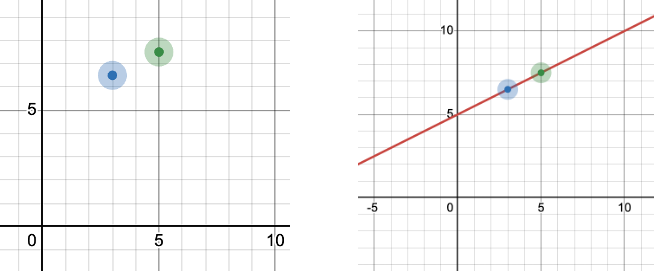
위 사진처럼 두개개의 점을 지나는 직선은 xy공간에서 바로 그릴 수 있다.
이를 ab공간으로 직선을 그으면 2개의 직선이 나온다.
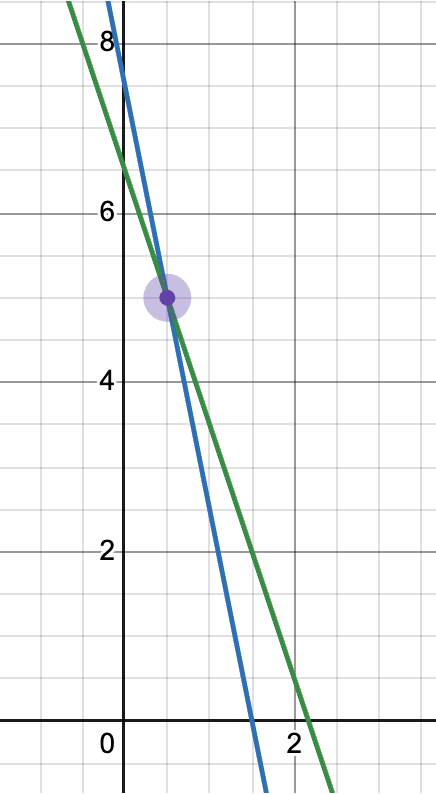
이 두 직선의 교점은 (a,b)는 바로 xy좌표의 기울기 a와 y절편인 b값이 된다.
하지만 직선이 ㅡ같은 y=5이거나 ㅣ같은 x=5라면?
이를 ab공간에서 나타내려면 의 개념이 들어가서 표현할 수가 없다.
그래서 원점과의 거리 와 각도 를 도입했다.

xy공간을 공간으로 표현할 수 있다.
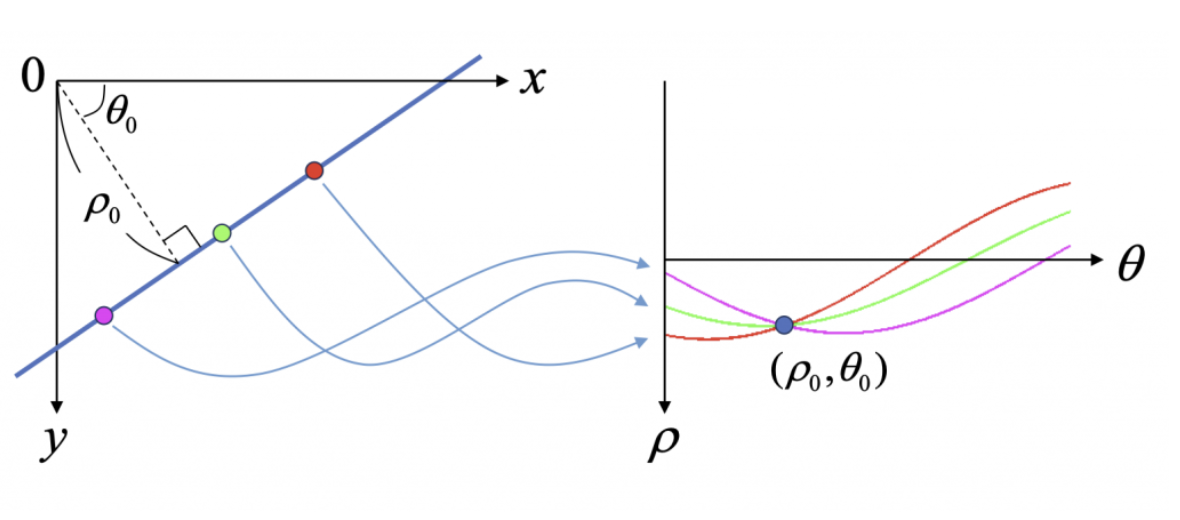
이렇게 되면 기존에는 표현할 수 없던 y=5는 , 으로 표현이 가능해진다.
점들이 모여 선이되기에, 나열된 픽셀들을 공간으로 나타내여 교점을 찾으면 그게 Line Detection인 것이다.
Circle Detection by Hough Gradient
원은 으로 3개의 파라미터를 가진다.
이를 허프 그래디언트 방법으로 원을 검출한다.
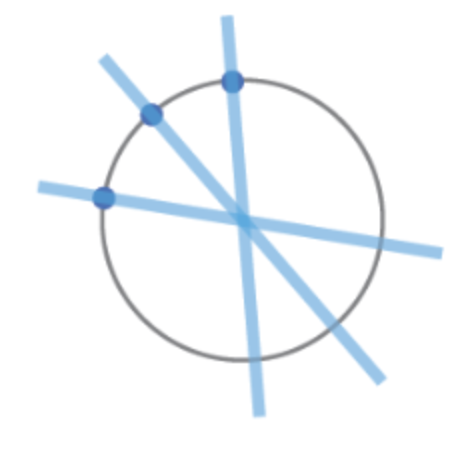
원의 점들에서 그래디언트 방향의 직선을 그린다.
직선이 겹치는 부분을 찾아 제일 많이 겹치는 부분이 원인 것을 알 수 있다.
