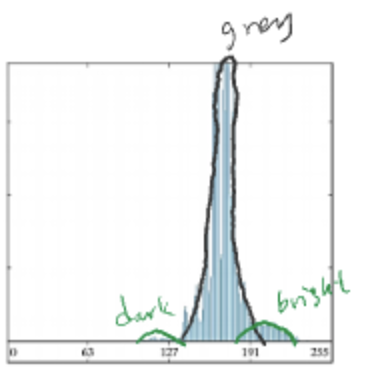
Segmentation

화면에 특정 부분을 분리하는 것을 컴퓨터비전에서 많이 봤을 것이다.

자율주행 자동차들은 사람과 도로, 나무, 벽 등을 구분해서 지나다닌다.

여기서 제일 중요한 것이 Segmentation 기술이다.

이미지 안에서 구역을 나눠 구분을 하는 것을 배워보자.

Global Thresholding

이때까지 Thresholding이라함은 $T$보다 작을땐 0 클땐 1 이런식으로 배웠다.

$g(x,y)=\begin{cases}1\quad if\;f(x,y) >T\\0 \quad if\;f(x,y)\le T\end{cases}$

$g(x,y)=\begin{cases}2\quad if\;f(x,y) >T_1\\1\quad if\;T_1\ge f(x,y) >T_2\\0 \quad if\;f(x,y)\le T_2\end{cases}$

Threshold는 여러개로 구역을 나눌 수도 있다.

아래에 Multiple Global Thresholding 참고.

Simple Iterative Technique

위와 같은 이미지를 2개의 영역으로 구분하려면 어떻게 알고리즘이 흘러갈까?

Principal

1. $T = T_0$로 초기값으로 초기화한다.
2. $C_1$이라는 $[0,T]$의 영역을 가진 클래스 구간을 나눈다.
3. $C_2$이라는 $[T+1,L-1]$의 영역을 가진 클래스 구간을 나눈다.
4. $C_1$의 평균 $m_1$, $C_2$의 평균 $m_2$을 구한다.
5. $m_1$과 $m_2$의 평균을 $T$에 대입한다. $T=\frac{m_1+m_2}{2}$
6. $\vert T_{new}-T\le \Delta T\vert$ 때까지 1~5의 과정을 반복한다.

Example

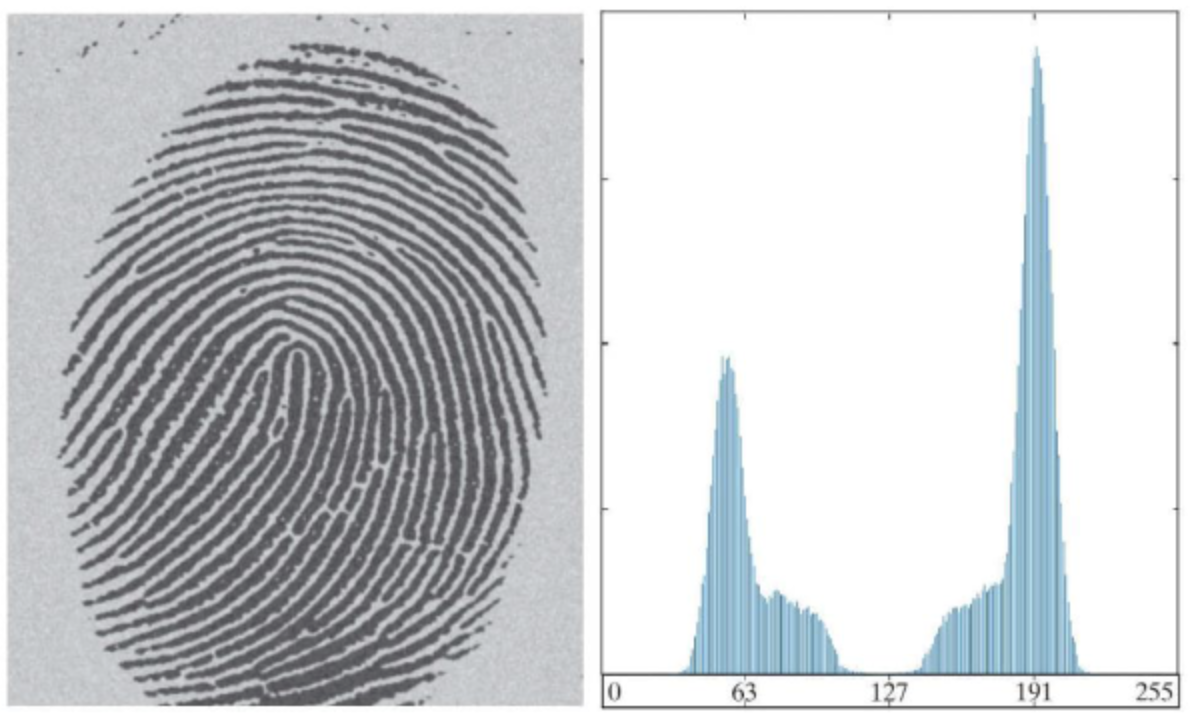
지문 사진과 사진의 히스토그램이 있다고 하자.

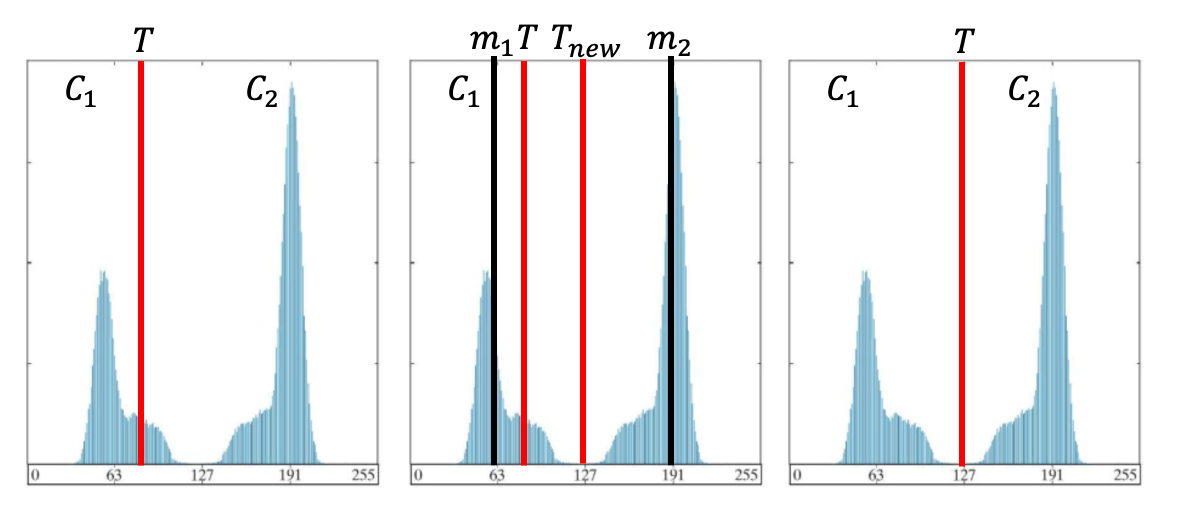
처음으로 $T$값을 아무데나 지정해 구간을 나눈다.

그 다음 각 구간에 대한 평균과 평균에 대한 평균($\frac{m_1+m_2}{2}$)을 새로운 $T_{new}$에 갱신한다.

이를 반복해 거의 움직이지 않는다면($\vert T_{new}-T\le \Delta T\vert$), $T$를 찾은 것이다.

하지만 이상적인 상황에서 딱 우리 눈으로 봤을때 쉬워보이는 히스토그램만 Segmentation한다는 단점이 있다.

Otsu's Method

그래서 Class간의 분산과 Class내부의 분산의 통계적인 개념을 도입한 방법이 있다.

Class 간의 분산이 크다는 것은, Class가 구분이 잘되어있다는 말이므로,

Class 간의 분산을 크게 최적화하는 것이 Otsu's Method이다.

Principal

• within class variance: $\sigma_W^2(k)=P_1(k)\sigma_1^2(k)+P_2(k)\sigma_2^2(k)$

• between class variance:
  $\sigma_B^2(k)=P_1(k)(m_1(k)-m_G)^2+P_2(k)(m_2(k)-m_G)^2\\=\sigma_G^2-\sigma_W^2(k)$

• $p(i)=\frac{n(i)}{MN}$, $m_G=E[i]=\sum_{i=0}^{L-1}ip(i)$,
  $\sigma_G^2=E[(i-m_G)]^2=\sum_{i=0}^{L-1}(i-m_G)^2p(i)$

여기서 $\sigma_B^2(k)$를 최대화한다는 것은 $\sigma_W^2(k)$를 최소화하는 것과 같다.

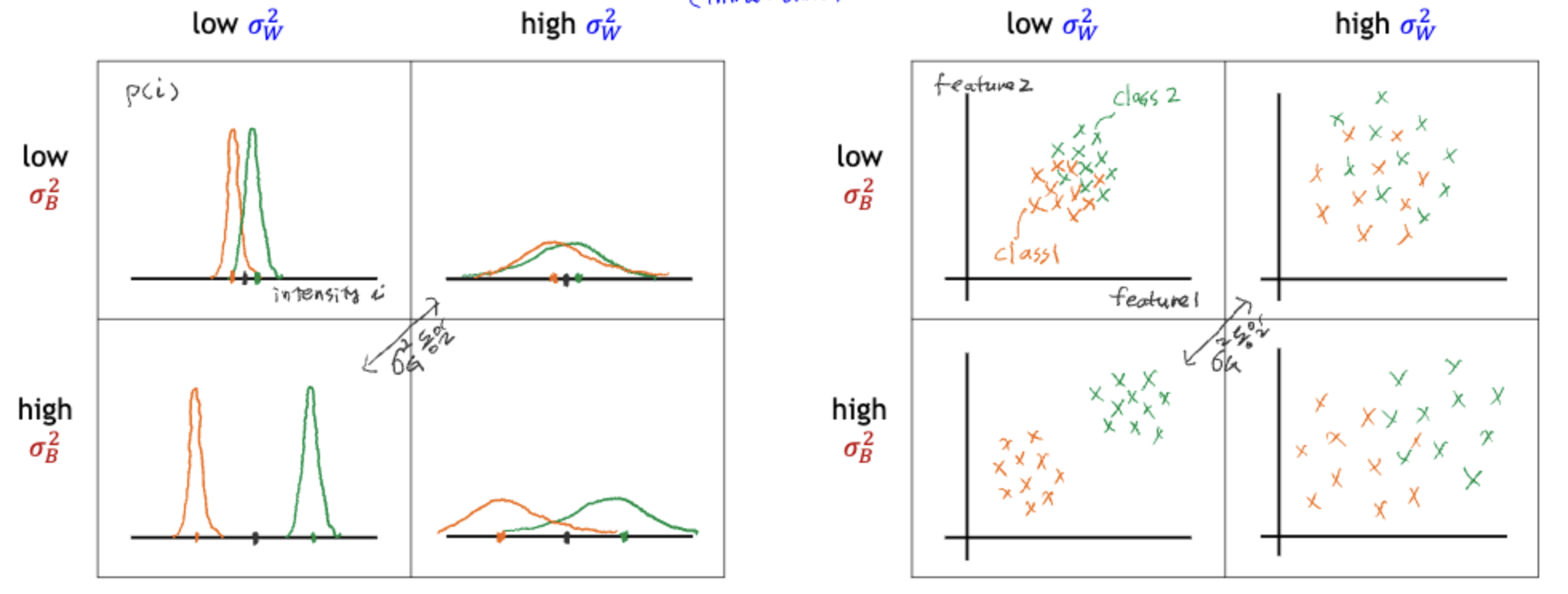
그림을 참고하면 이해하기 쉽다.

클래스 내부 분산이 작으면 군집의 너비가 좁아지고, 분산이 크다면 넓어진다.

클래스 간 분산이 작으면 군집끼리의 거리가 좁아지고, 분산이 크다면 멀어진다.

$P(C_1)=P_1(k)=\sum_{i=0}^kp(i)$이므로

$P(C_2)=P_2(k)=\sum_{i=k+1}^{L-1}p(i)$는 $1-P_1(k)$와 같다.

왜냐면 $P(C_1)+P(C_2)=1$이기 때문이다.

아까 언급한 클래스 내부 분산의 식은 다음과 같다.
$\sigma_W^2(k)=P_1(k)\sigma_1^2(k)+P_2(k)\sigma_2^2(k)$

그리고 클래스 간 분산의 식은 $\sigma_B^2(k)=\sigma_G^2-\sigma_W^2(k)\\=P_1(k)(m_1(k)-m_G)^2+P_2(k)(m_2(k)-m_G)^2\\=P_1(k)P_2(k)(m_1(k)-m_2(k))^2$

여기서 $P_1(k)+P_2(k)=1$ 이므로 $P_1(k)=P_2(k)=0.5$로 갈때 최대값을 가진다.

또한, $(m_1(k)-m_2(k))^2$은 클래스 간의 거리제곱으로도 볼 수 있다.

두 클래스의 너비(분산)이 거의 같아지고, 두 클래스 간의 거리가 커지면 최적화 된다는 것이다.

$P_1(k)P_2(k)(m_1(k)-m_2(k))^2\\=\frac{(m_GP_1(k)-m(k))^2}{P_1(k)(1-P_1(k))}$ 로 $P_2$를 제거한 $P_1$에 관한식으로 유도할 수 있다.

$\eta(k)=\frac{\sigma_B^2(k)}{\sigma_G^2}$ $(0\le\eta(k)\le1)$로 나타내어 $\eta(k)$를 1에 가깝게 만들도록 최적화한다.

$\max_{0\le k\le L-1}\sigma_B^2(k)=\max_{0\le k\le L-1}\frac{(m_GP_1(k)-m(k))^2}{P_1(k)(1-P_1(k)) }$로 $P_2$를 안구해도 되는 식을 써보자.

1. 모든 $i$에 대한 $p(i)$를 구한다.
2. $m_G$를 구한다.
3. 모든 $0\le k\le L-1$에 대한 $P_1(k)$, $m(k)$, $\sigma_B^2(k)$를 구한다.
4. $\sigma_B^2(k)$들 중 최대가 되는 k가 최적의 $T$이다.

Example

위 같은 노이즈가 심한 이미지가 있을 때는 당연히 뭐 먼저한다?

Low pass Filtering으로 노이즈를 제거해야한다.

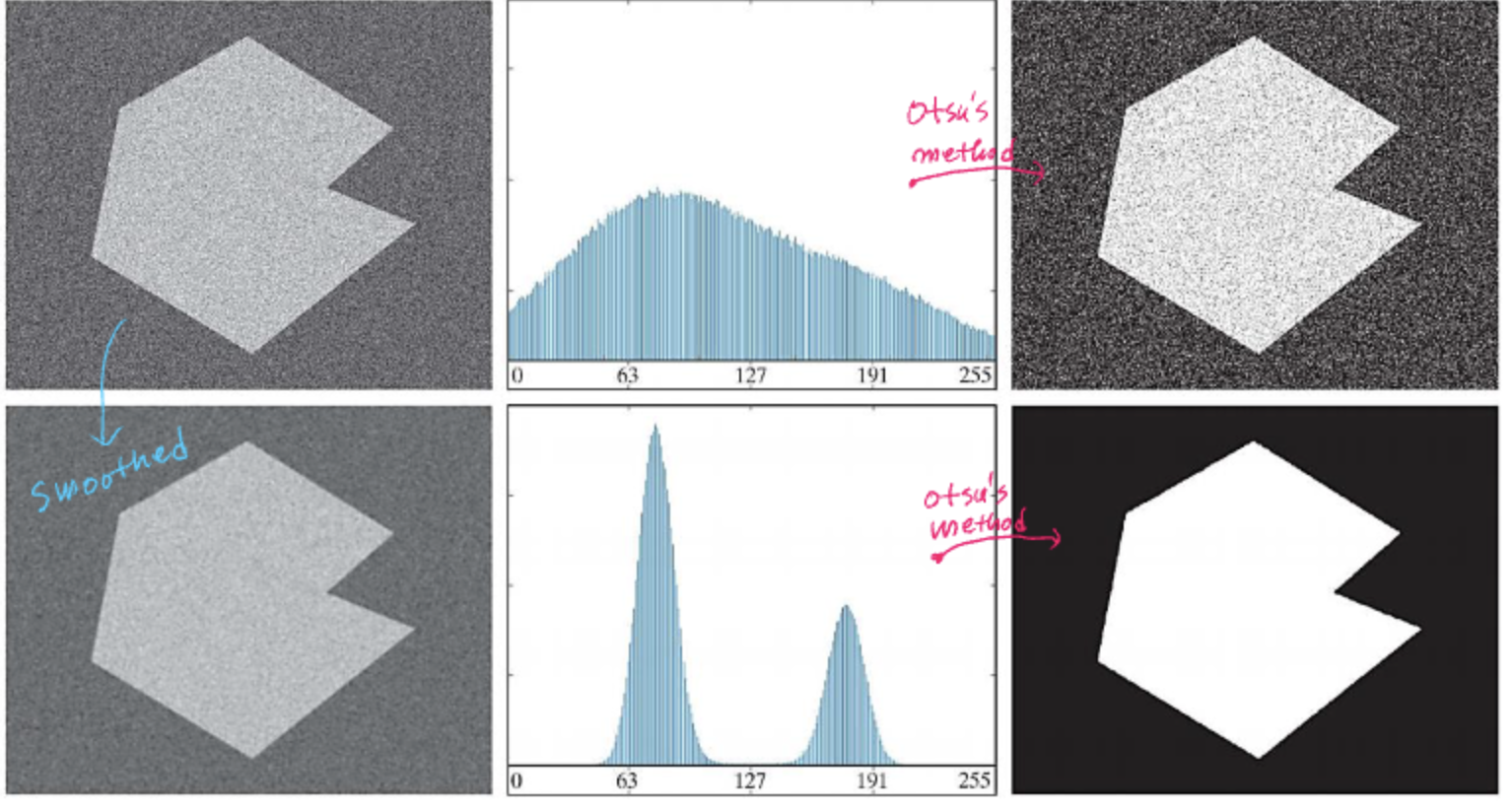
Smoothing을 진행하고 Otsu's Method를 거쳐 Segmentation을 하면 된다.

Using Edges

하지만 클래스간의 간격이 매우 좁고, 가운데 클래스의 피크가 너무 커서

주변의 다른 클래스와 구분이 안가는 경우가 있을 수 있다.

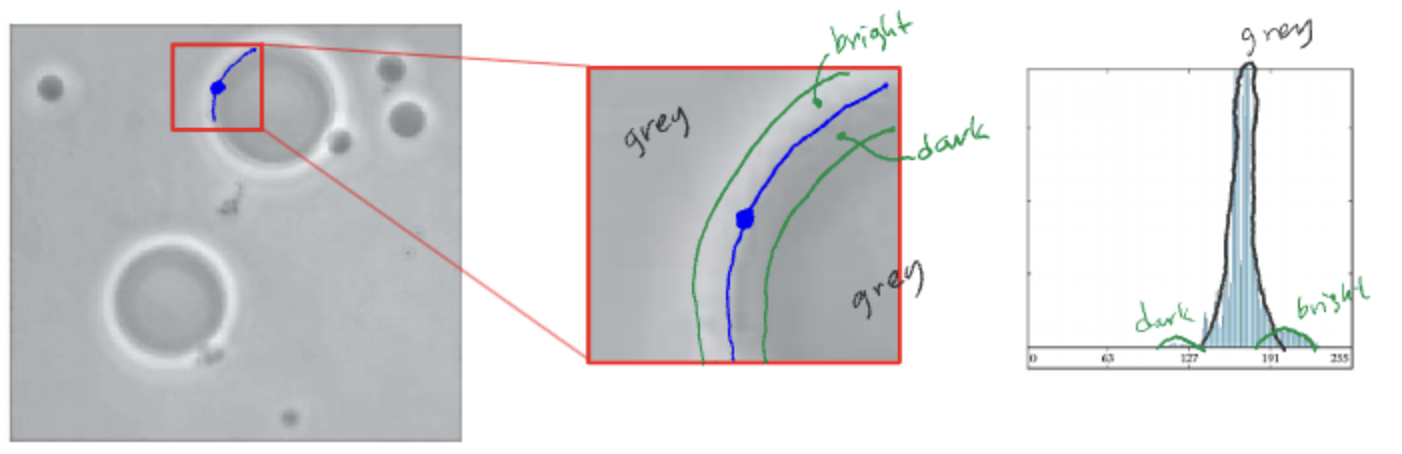
히스토그램만 보면 클래스가 단 하나로 판단할 수도 있다.

이때는 엣지만의 데이터를 검출해서 엣지안의 데이터만 보고 Segmentation을 실행한다.

Principal

1. Laplacian이나 magnitude of the gradient 를 이용해서 엣지를 검출한다.
2. 엣지 이미지 내에서 히스토그램을 그린다.
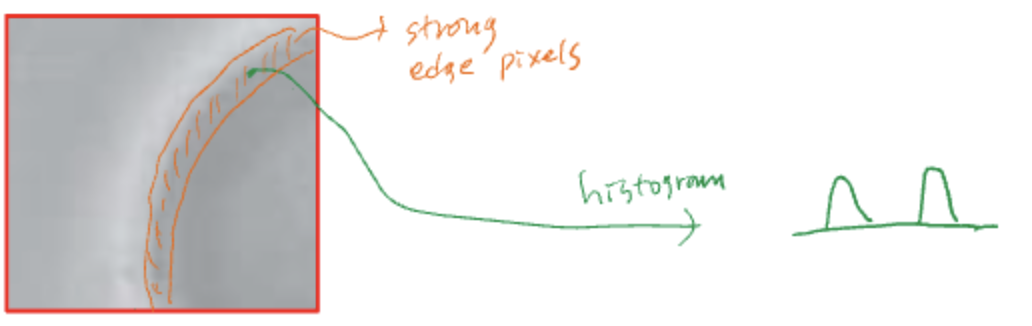
3. 구분이 어려웠던 히스토그램이 간단해졌으므로, 여기서 Otsu's Method를 쓴다.

Example

회색 배경에 아주작은 흰 점의 이미지가 있다고 하면, 히스토그램은 다음과 같다.

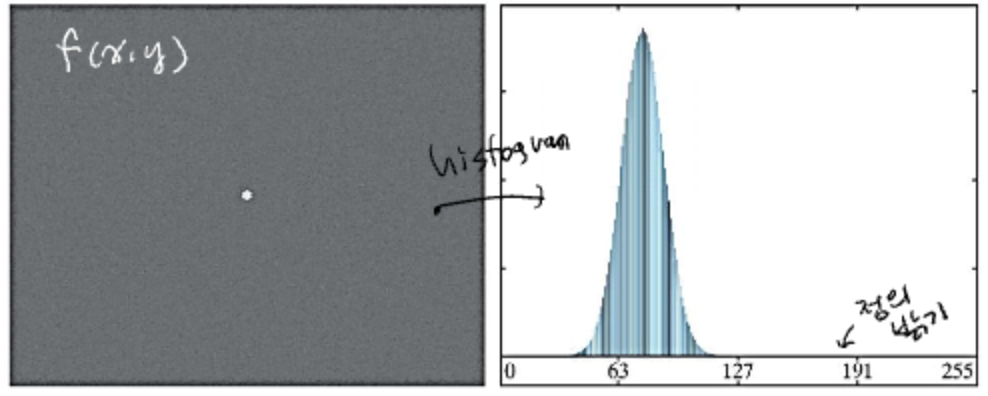
점이 매우 작기때문에 히스토그램에서는 무의미한 점의 밝기가 표현된다.

이러한 이미지에 Edge를 검출하는 $g_N$을 취하면 다음의 히스토램의 분포처럼 변한다.

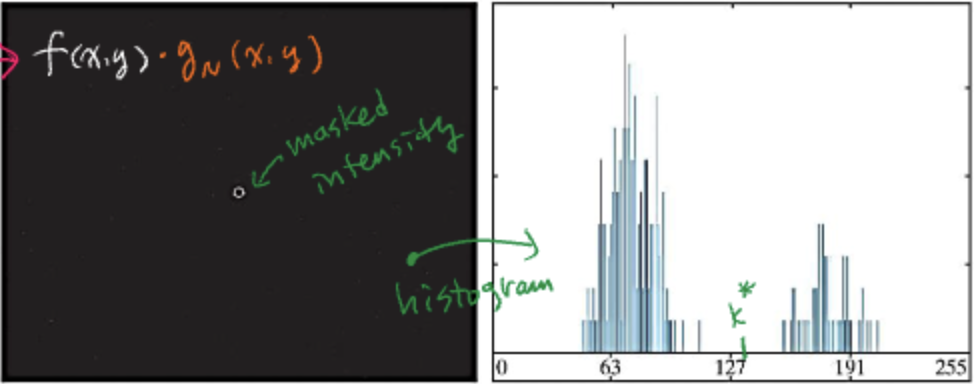
히스토그램에서 점의 밝기가 증폭된 것처럼 변환이 된다.

왜냐하면 Edge만을 검출했기 때문에, Edge 주면의 값만 히스토그램에 나타나기 때문이다.

저 히스토그램으로 Otsu's Method를 진행한다.

cv2.threshold()

OpenCV에는 threshold()라는 함수로 이미지에 Global Threshold를 적용할 수 있다.

type으로 다음의 종류를 가진다.

우리가 배운 Otsu's Method의 Threshold를 자동으로 정해주는 기능도 있다.

Multiple Global Thresholding

Threshold가 여러개있는 것이다.

이를 Otsu's Method에 적용해보자.

2 classes(1 Thresholds)

$\sigma_B^2(k)=P_1(k)(m_1(k)-m_G)^2+P_2(k)(m_2(k)-m_G)^2$

$P_1(k)=\sum_{i=0}^kp(i)$, $P_2(k)=\sum_{i=k+1}^{L-1}(1-p(i))$

$m_1(k)=\sum_{i=0}^ki\frac{p(i)}{P_1(k)}$, $m_2(k)=\sum_{i=k+1}^{L-1}i\frac{(1-p(i))}{P_2(k)}$

K classes(K-1 Thresholds)

$\sigma_B^2=P\sum_{k=1}^KP_k(m_k-m_G)^2$

$P_k=\sum_{i\in c_k}p_i$

$m_k=\frac{1}{P_k}\sum_{i\in c_k}ip_i$

뭐 수식은 복잡하지만 별거 없다.

왼쪽이 2Classes, 오른쪽이 Multiple Threshold라고 보면 저 수식이 이해가 될 것이다.

Local Thresholding

실제 사진을 찍으면 음영차가 있는 경우가 있다.

스도쿠에서 Thresholding을 적용해서 밝게 적용하고 싶다고 할때

Global Thresholding을 적용해버리면 사진이 타노스마냥 반토막 날 수도 있다.

그래서 이미지를 나눠서 Thresholding을 적용하는 것을 Local Thresholding이라고 한다.

방법은 크게 3가지가 있다.

Partitioning

첫 번째 방법인만큼 간단하다.

1. 이미지를 히스토그램으로 바로 나타내면, 어디가 class인지 구분하기 어렵다.
   

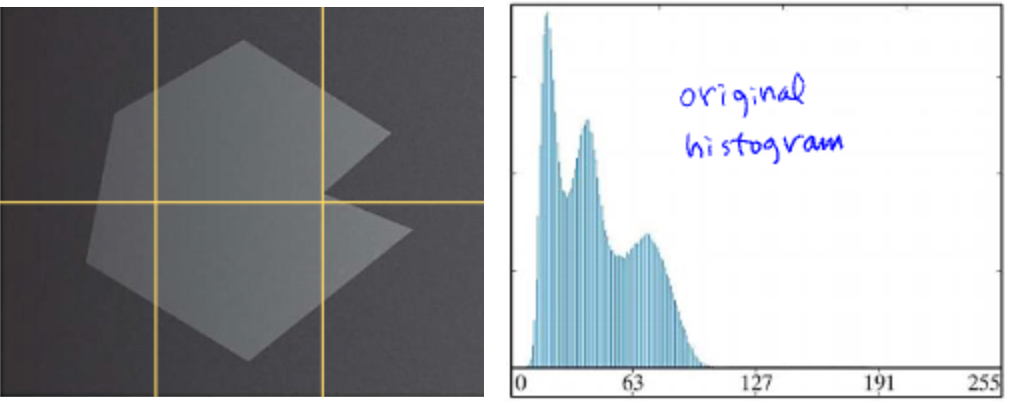
2. 이미지를 원하는 개수만큼 sub image로 나누고 각 구간별로 히스토그램을 그린다.

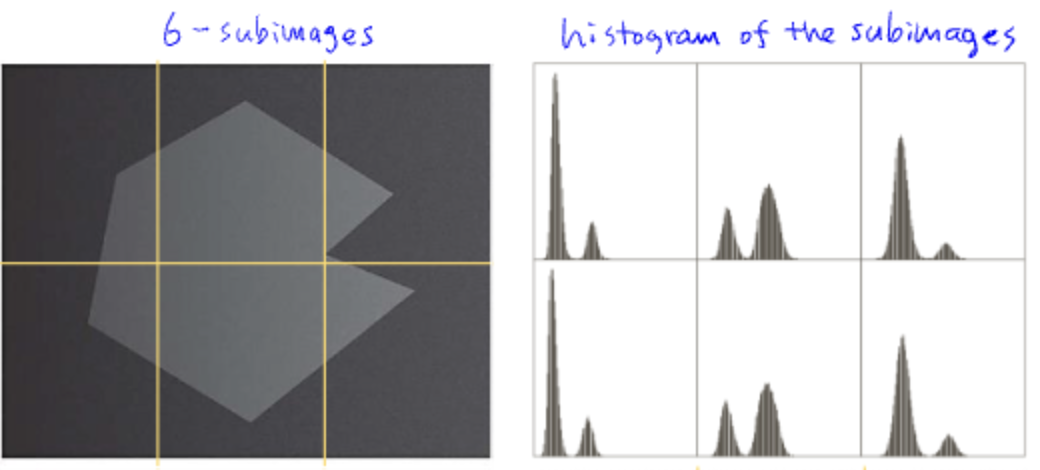
3. 히스토그램별로 Otsu's Method 를 적용하여 최종 이미지로 합친다.
   

Local Statistics

가장 많이 쓰이는 방법으로 통계적 관점으로 접근한다.

이미지를 (0,0)부터 (M-1, N-1)픽셀까지 3x3, 5x5, ... 마음대로 주변 픽셀을 관찰한다.

마치 Convolution에서 주변 픽셀을 관찰하는 것처럼 말이다.

자신을 포함해서 주변픽셀들 $S_{xy}$의 평균 $m_{xy}$과 표준편차 $\sigma_{xy}$를 구한다.

$S_{xy}$에 대한 local threshold $T_{xy}=a\sigma_{xy}+bm_{xy}$로 정한다.

임계값보다 작으면 0, 크면 1을 적용한다.

Moving Averages

Local Statistics는 평균과 표준편차를 쓴다면, Moving Averages는 평균만 사용한다.

$T_{xy}=bm_{xy}$로 정한다.

Example

주변은 어둡고 가운데가 밝은 이미지도 잘 검출해낸다.

1111 자로 어두운 영역 또한 맛있게 걸러낸다.

P.S. 글씨체를 검출할 때는 글씨체의 두께(stroke)픽셀의 5배정도로 윈도우 사이즈 $n$을 잡는게 좋다고 한다.

cv2.adaptiveThreshold()

OpenCV 에서는 threshold가 local별로 다르기 때문에 적응형 임계값이라고 한다.