Template Matching
Overview
입력 영상에서 일부분의 영상 위치를 찾아낼 때 사용하는 기술이다.
Template은 일부분의 영상을 의미한다.
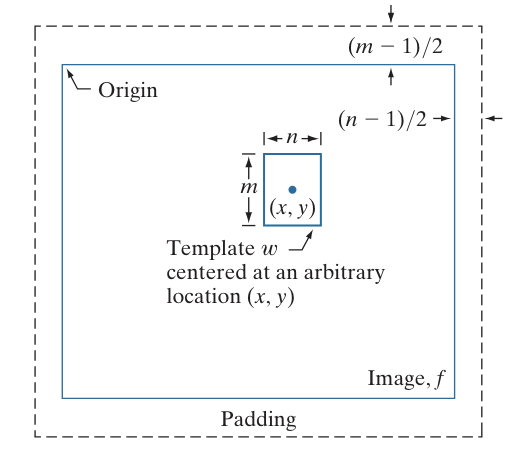
이미지에서 template의 절반크기만큼 padding을 주어서 index out of range가 없도록 한다.
그리고 위에서부터 탐색해서 유사한지 유사하지 않은지 판단하는 것이다.
Matching Criteria
유사한지에 대한 것은 Similarity, 유사하지 않은지에 대한 것은 Dissimilarity로 판단한다.
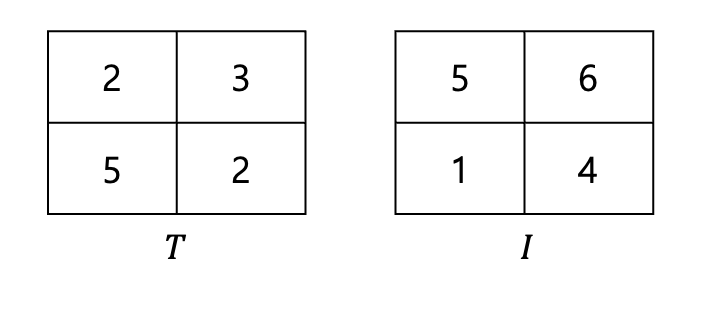
왼쪽이 Template, 오른쪽이 현재 탐색중인 원본 이미지의 일부라고 하자.
Dissimilarity
비유사도는 Sum of Squared Error/Difference(SSE/SSD), Sum of Absolute Error/Difference(SAE, SAD)로 있다.
SSE/SSD
모든 픽셀들에 대해 템플릿과 원본 이미지에 대한 l2-norm을 구하고 합한 것이다.
R(x,y)=∑x′,y′(T(x′,y′)−I(x+x′,y+y′))2=E((T−I))2=μe2
여기서는 (2−5)2+(3−6)2+(5−1)2+(2−4)2=38이다.
SAE/SAD
l1-norm으로 맨허튼 거리를 구하고 합한 것이다.
R(x,y)=∑x′,y′∣T(x′,y′)−I(x+x′,y+y′)∣=E((T−I))2=μ∣e∣
여기서는 ∣2−5∣+∣3−6∣+∣5−1∣+∣2−4∣=12이다.
비유사도는 높을 수록 유사하지 않음이 큼을 의미하므로, 이 값이 제일 작은 곳으로 템플릿 매칭을 한다.
Similarity
유사도는 통계학적 관점으로 접근한다.
템플릿은 사용자가 찾고 싶은 대상이고, 원본 이미지도 늘 바뀐다.
즉 T, I를 랜덤변수로 생각하고 2개에 대해 공분산이나 상관계수 이런것을 구하면 그게 곧 유사도일 것이다.
Correlation
상관계수(Correlation Coefficient)를 구하게 위핸 Correlation이 필요하기 때문이 구한다.
Correlation=∑x′,y′T(x′,y′)⋅I(x+x′,y+y′)=E(T⋅I)
위 사진에선 각 픽셀끼리의 곱의 합이므로 41이 된다.
Covariance
각 랜덤변수의 평균을 따로 구한다. 그리고 각 랜덤변수의 픽셀별로 평균과의 차를 구한다.
그리고 그 차를 서로 곱하고 더한다. 그림으로 설명하면 다음과 같다.
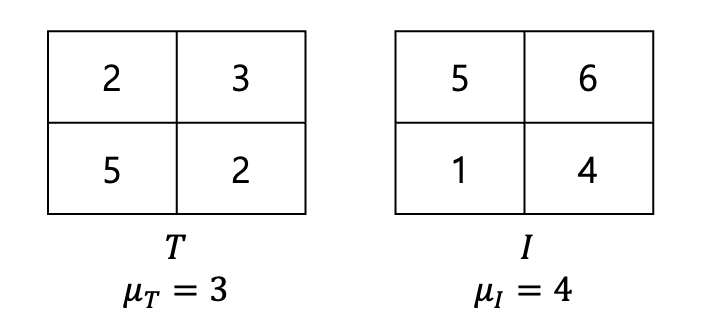
μT=42+3+5+2=3,μI=45+6+1+4=4이다.
이를 기존 랜덤변수에 모두 뺀다.
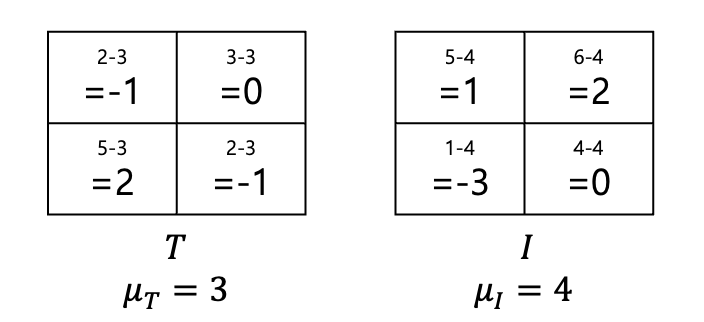
그리고 이 값들을 다시 서로 곱해서 더한다.
(−1×1)+(0×2)+(2×−3)+(−1×0)=−7
수식으로 표현하면 다음과 같다.
T′(x′,y′)=T(x′,y′)−픽셀수1∑x′′,y′′T(x′′,y′′)
I′(x+x′,y+y′)=I(x+x′,y+y′)−픽셀수1∑x′′y′′I(x+x′′,y+y′′)
Covariance=∑x′,y′T(x′,y′)⋅I′(x+x′,y+y′)
Correlation Coefficient(Covarince를 정규화한 것)
R(x,y)=sumx′,y′T′(x′,y′)2⋅sumx′,y′I′(x+x′,y+y′)2Covariance=E{(T−μT)2}E{(I−μI)2}E{(T−μT)(I−μI)}
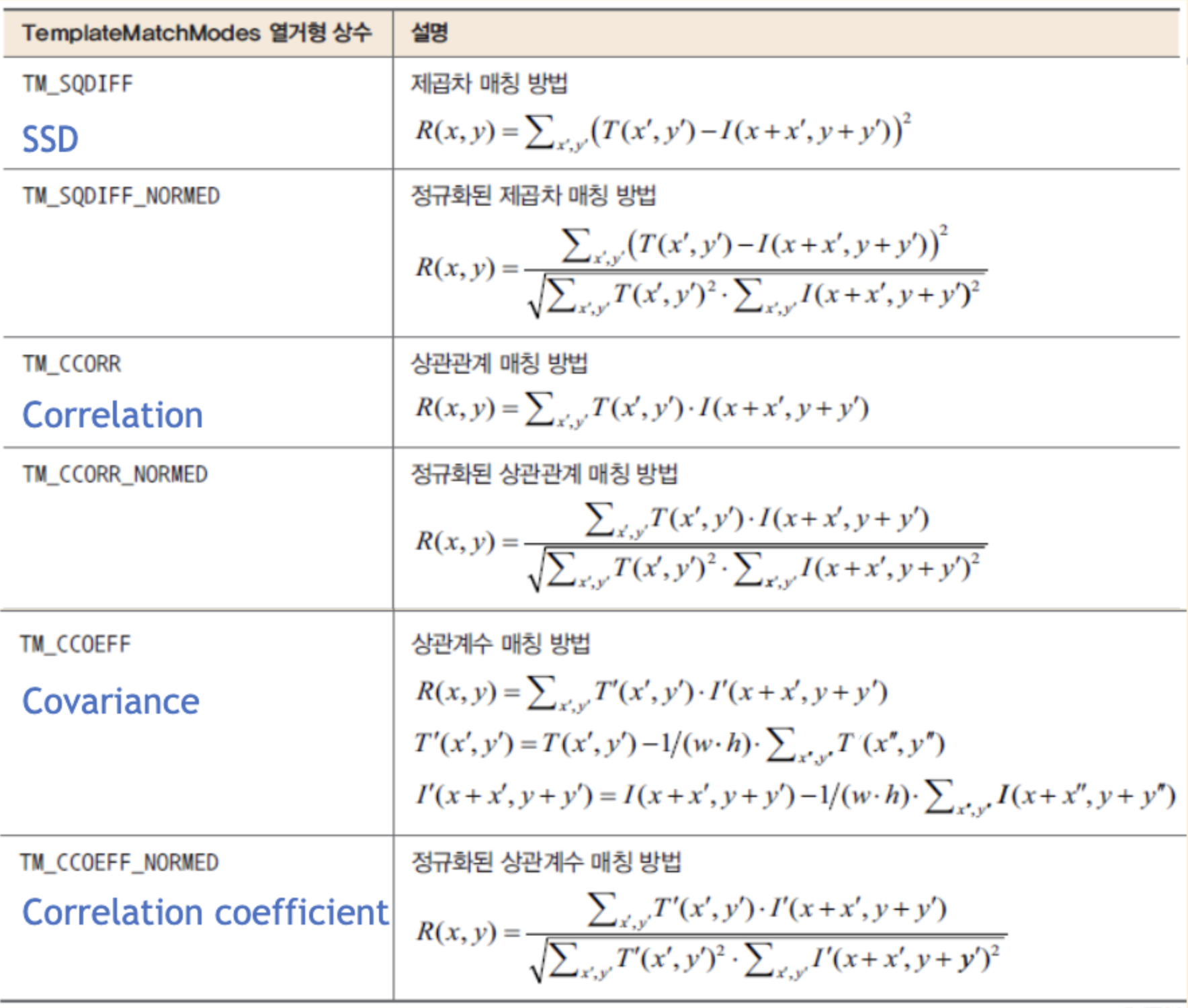
cv2.matchTemplate()

int method로 방금 배운 방법들의 종류가 있다.