Geometric Objects

흔히 들어본 Unity 게임 엔진이 있다. 이 엔진의 UI는 어떻게 생겼을까?

대부분 이런식의 UI를 본 적이 있을 것이다. 이러한 그래픽 데이터는 엔진이 그림을 그려주는 것일까?

반은 맞고 반은 틀리다. 사실은 OpenGL같은 그래픽스 API에서 계산을 도와준다.

앞에서 배웠던 Translate, Rotate, Projection 등등을 말이다.

그러면 이 OpenGL이 연산하는 내부구조를 알아야 그래픽스를 다뤘다고 볼 수 있다.

즉 기하를 알아야하는 것이다. 이번 장은 기하에 대해서 자세히 알아보자.

Scalar, Point, Vector

• Scalar
  실수 그 자체를 의미하며 정량적인 것을 나타낼 때 사용
• Point
  공간(길이도, 면적도, 부피도 없음)을 차지하지 않는 어느 특정 위치
• Vector
  방향과 그 방향으로 얼마나 크기를 나타내는지에 대한 척도
• Vector space
  존재가능한 요소 : Scalar, Vector
  가능한 연산 : 벡터-벡터 합, 벡터-스칼라 배
• Affine space
  존재가능한 요소 : Scalar, Vector, Point
  가능한 연산 : 벡터-벡터 합, 벡터-스칼라 배, 벡터-점 합, 점-점 빼기

벡터-벡터 합

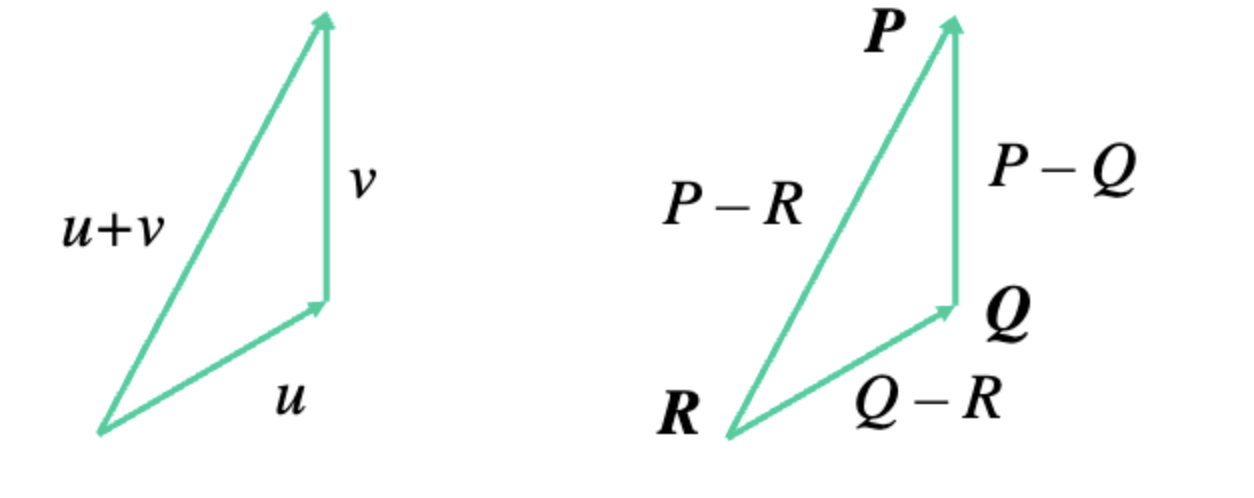
빼기는 벡터를 뒤집은($P$벡터가 있다면 완전 180도 반대인 $-P$를 더한) 것이므로 합이라고 표현한다.

벡터-스칼라 배

벡터의 방향은 일정하나, 그 크기가 달라진다.

크기가 0이고 방향이 없는 벡터는 영벡터(Zero vector)라고 부른다.

Line

초등학교 때 선이라는 개념을 배우는데, 2가지로 배웠을 것이다.

잘 기억이 안나는가? 알려주자면 직선과 선분이다.

직선은 시작지점과 종료지점이 없는 끝없는 선이며, 선분은 시작지점과 종료지점이 있는 선이라고 배웠을 것이다.

이 선을 Point와 Vector 그리고 Scalar로 표현할 수 있다.

아까 위 3 요소가 있으면 무슨 공간이라고 했냐면, 바로 Affine space이다.

$P(\alpha) = P_0 +\alpha d$
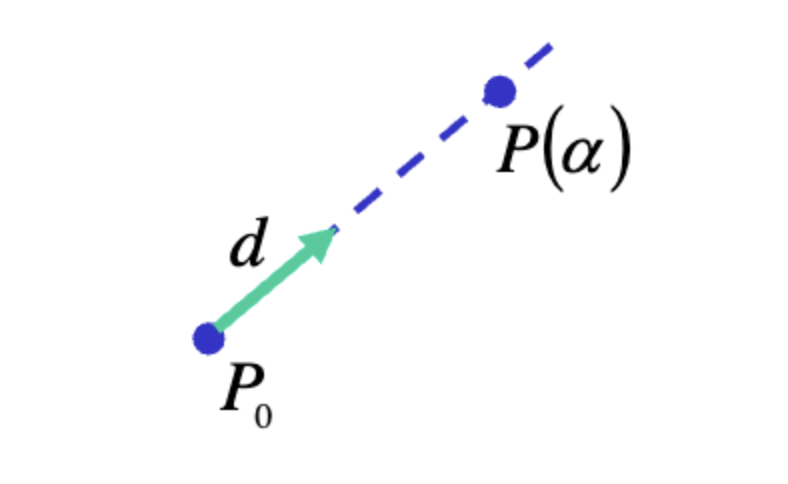
점 $P_0$부터 시작해서 벡터 $d$의 방향으로 정의되는 직선이 되겠다.

Affine addition(sum)

점 $Q$, 스칼라 $\alpha$, 벡터 $v$가 있을 때,

$P(\alpha)=Q+\alpha v$는 선분이라고 직전에 설명하였다.

아래 그림의 상황을 보자.

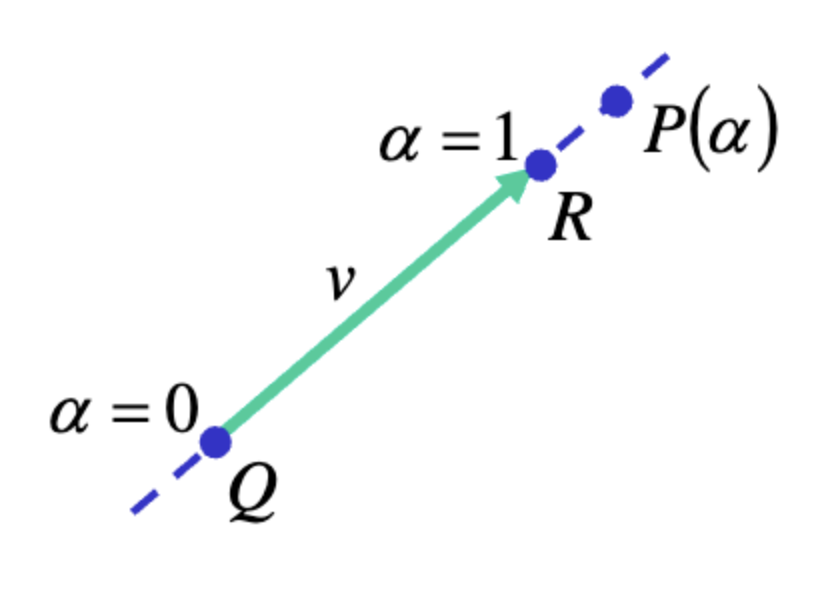
벡터 $v$는 점과 점의 빼기로도 표현이 가능하다. $v = R - Q$를 선분방정식에 대입하면?

$P(\alpha) = Q + \alpha(R-Q)=\alpha R+(1-\alpha)Q$가 된다.

$\alpha$를 $\alpha_1$, $1-\alpha$를 $\alpha_2$라고 두면, $P=\alpha_1R+\alpha_2Q(단, \alpha_1+\alpha_2=1)$이 된다.

이게 무슨 식일까? 바로 중학교 때 배웠던 선의 내분점이다.

두 알파의 합이 1이면, 딱 점 $Q$와 점 $R$을 잇는 그 사이의 공간이 정의된다.

바로 시작, 종료지점이 있는 선분이 생기는 것이다.

Convexity(볼록함)

Convexity는 볼록함을 의미하는데, Convex object는 무슨 뜻일까?

구나 별같은 도형을 생각했으면 오산이다.

기하학적 관점에서 Convex object는 다음과 같이 정의한다.

도형 내부에서 아무 두점을 선택했을 때, 그 두 점사이의 내분점이 그 도형안에 있어야한다.

해안가를 생각 해보자.

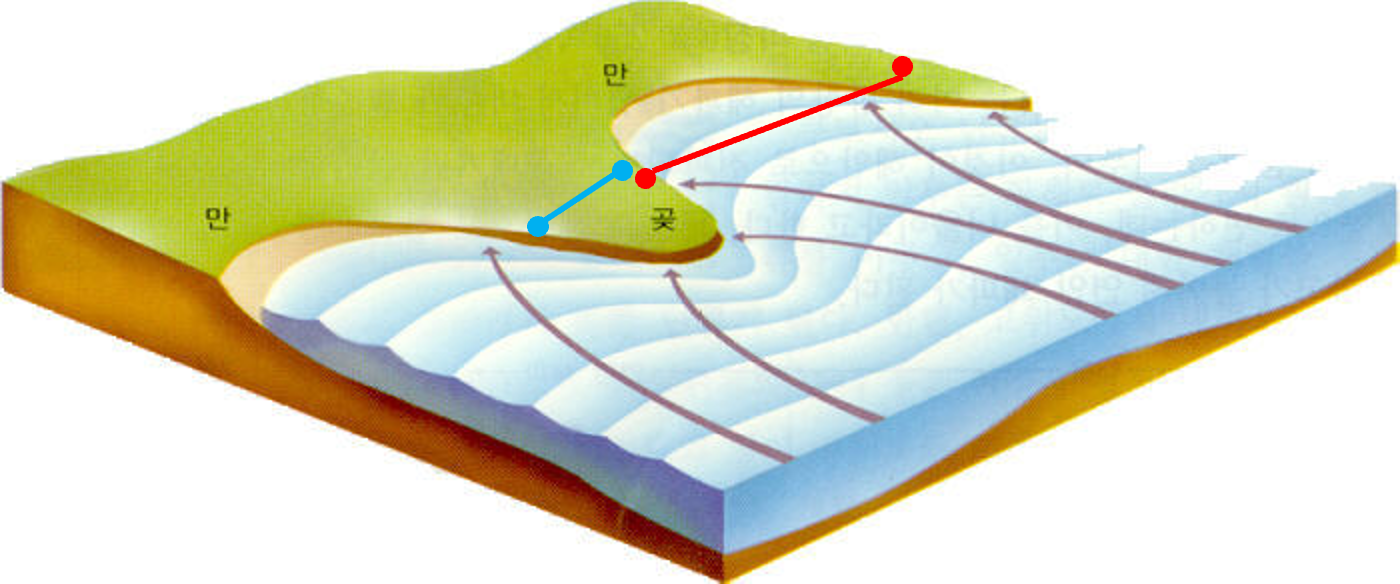
볼록하게 튀어나오는 곳은 곶, 안으로 파진 곳은 만이라고 한다.

위의 정의를 적용하면, 곶 내부에서 아무 두점을 선택했을 때, 그 두 점사이의 공간이 그 도형안에 있어야하는 것이다.

위의 파란 점을 보면 내분점이 존재해야할 공간은 항상 곶 내부에 있다.

즉 곶은 Convex Object이다.

하지만, 만은 내부에서 아무 두점을 선택했을 때, 그 사이의 공간이 바다이다.

정의를 만족하지 못하기에 Convex하지 않다고 볼 수 있다.

Convex hull

$P=\alpha_1P_1+\alpha_2P_2+\dots+\alpha_nP_n\\(단, \alpha_1+\dots+\alpha_n=1, \alpha_i\geq1,i=1,\dots,n)$
위를 만족하는 도형중 $n$을 최소화 한 도형을 Convex hull이라고 한다.

즉 꼭짓점 여러개로 만든 Convex Object라고 생각하면 이해하기 쉽다.

Dot Products

Dot Products(내적)은 뒤 벡터를 앞 벡터에 투영했을 때의 크기와 뒤 벡터의 크기의 곱으로 정의된다.

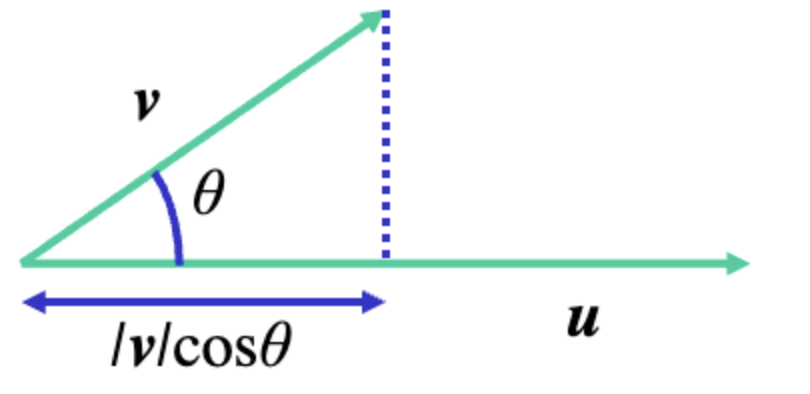
벡터 $u$를 앞 벡터, 벡터 $v$를 뒤 벡터라고 정의하자.

그렇다면 $u\cdot v=\vert v\vert cos{\theta}\times u$인 것이다.

Cross Products

Cross Products(외적)은 두 벡터로 생성된 공간(면)의 수직방향으로 정의된다.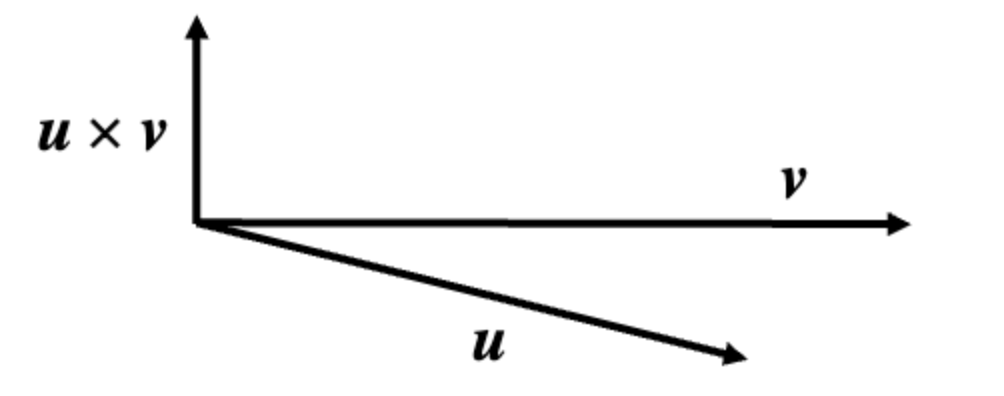

Plane

면은 선을 움직인 흔적으로 생긴 공간을 의미한다.

선은 점을 움직인 흔적으로 생긴 공간이다.

아까 선은 점에 벡터를 더한 방정식으로 표현하였으므로,

면 또한 점과 벡터를 잘 건드려서 방정식으로 표현할 수 있다.

Normal to the plane

면의 방향은 Cross Products와 같은 말이다.

색종이를 책상 위에 올렸다고 하자. 이 색종이의 방향은 수직인 방향인 위쪽을 의미하는 것이다.

Coordinate Systems

3차원 좌표계는 어떻게 이루어져있을까?

서로서로 영향을 주지 않는 축 x, y, z축이 있고, 원점이 있을 것이다.

선형대수학에서는 서로 영향을 주지 않는 축을 독립적인 관계라고 설명한다.

또한 이런 독립적인 성질을 가진 축들을 기저(basis)라고 부른다.

비유해서 설명하자면

이 빨간색, 초록색, 파란색 벡터(행렬)은 서로 독립적이며, 기저인 것이다.

Rotate

이전 챕터에서 배운 Transform 중 하나인 Rotate는 3차원 공간에서 어떻게 연산되는 것일까?

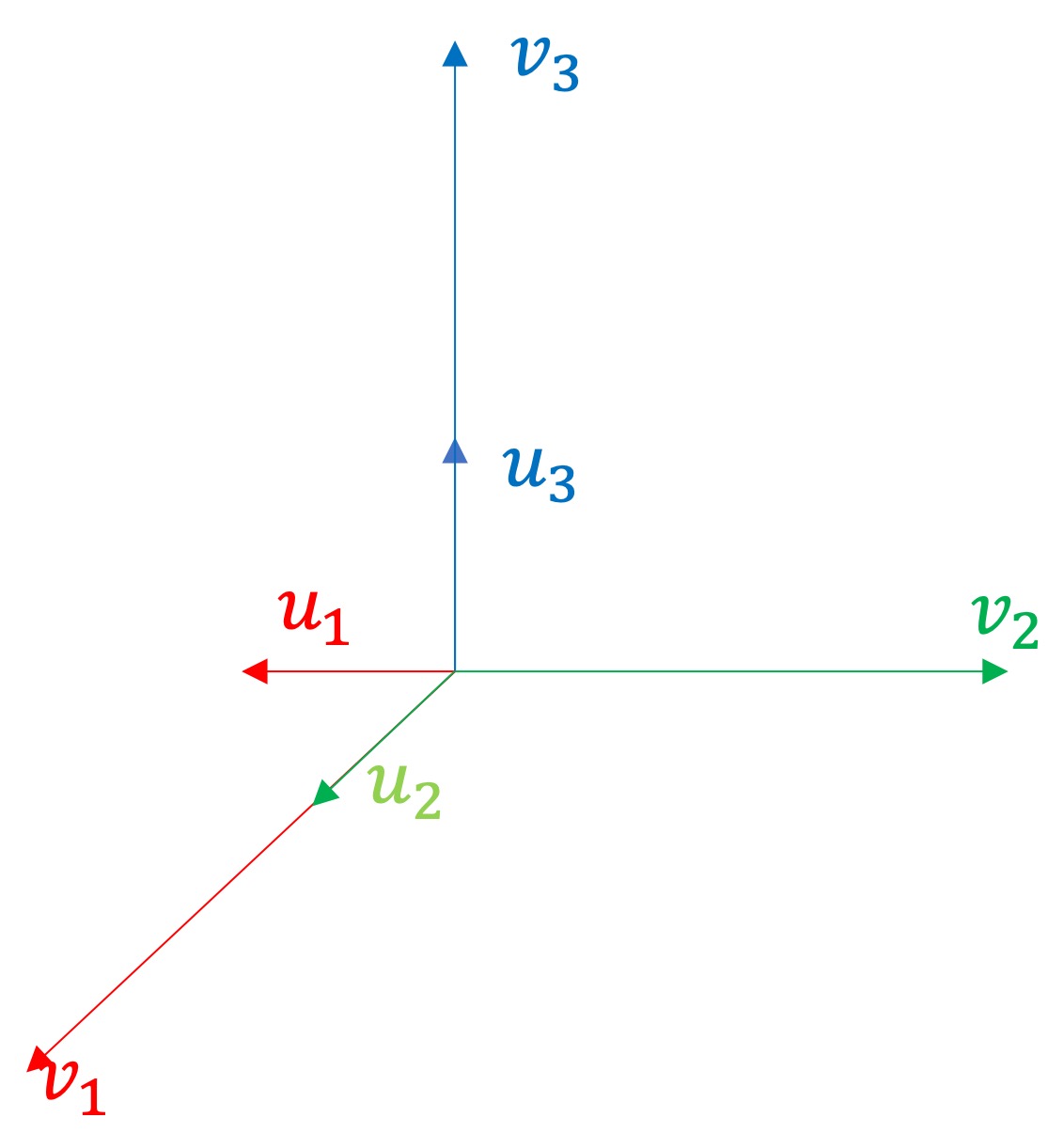
다음과 같이 u에 대한 좌표계와 v에 대한 좌표계가 있다고 치자.

(기저집합 {$v_1,v_2,v_3$}, {$u_1,u_2,u_3$})

$u_1 = -v_2, u_2 = v_1, u_3 = v_3$으로 표현된다.

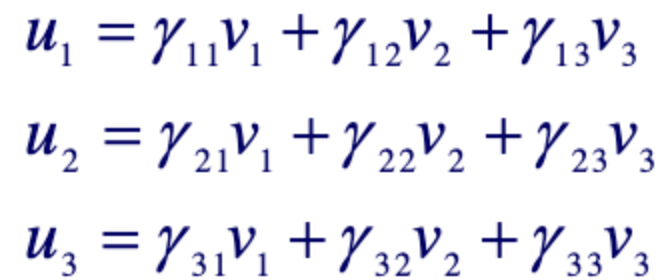
이를 계수 행렬 $M$로 표현해서 다음의 꼴로 나타내면

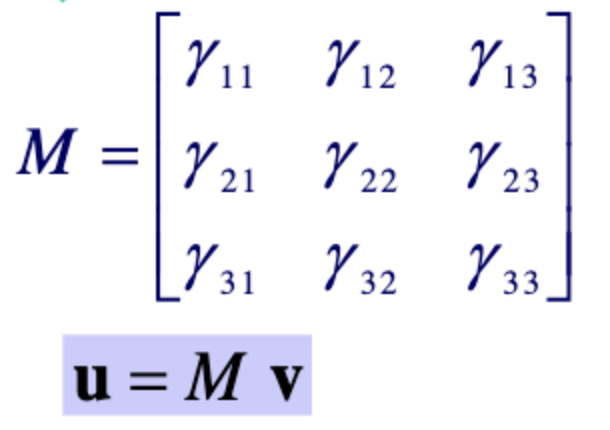
위의 식으로 표현할 수 있다.

즉, $u_1 = -v_2, u_2 = v_1, u_3 = v_3$인 예시 상황은 $M = \begin{pmatrix}0&-1&0\\1&0&0\\0&0&1\end{pmatrix}$인 것이다.

기저(축)가 바뀌는 상황

1. 원점이 변하지 않는 것
   Scaling(크기 축소 확대), Rotation(회전)
   
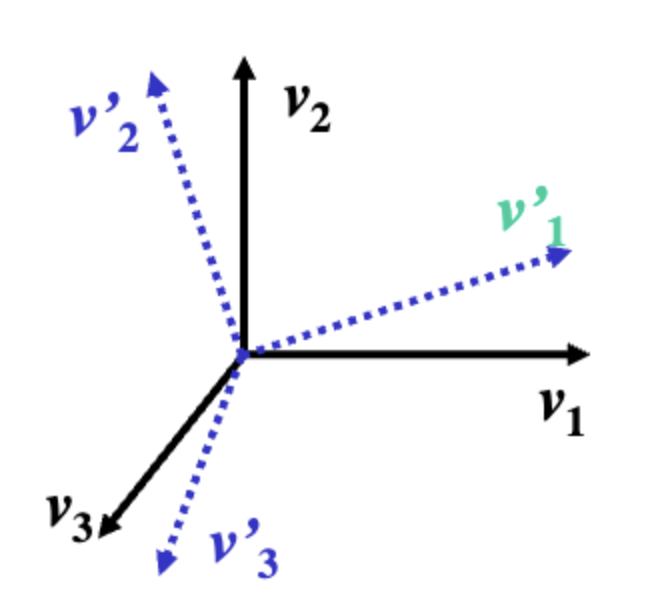
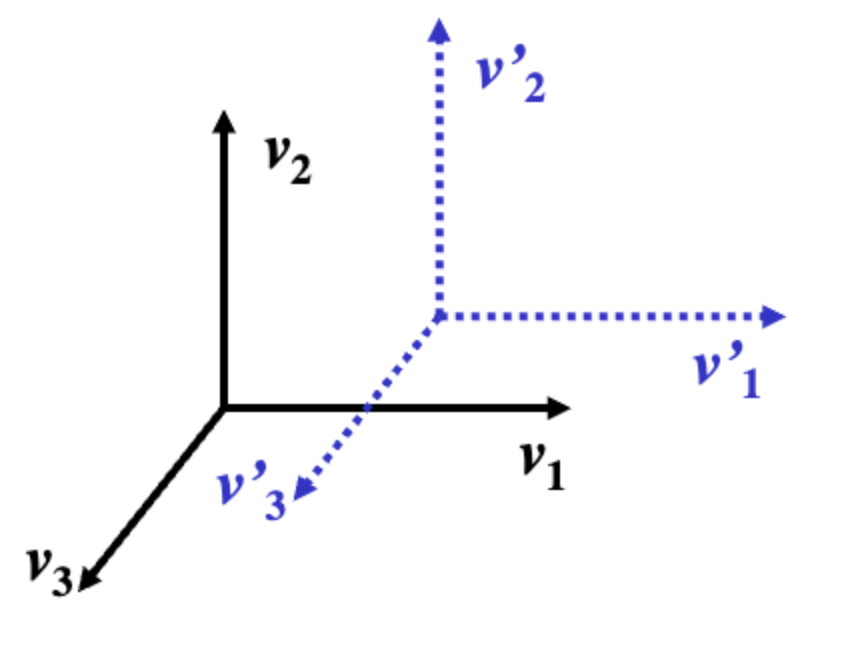
2. 원점이 변하는 것
   Translation(평행 이동)
   

예제

좌표계 $v_1=[1,0,0]^T, v_2=[0,1,0]^T, v_3=[0,0,1]^T$와
다음의 관계를 만족하는 새로운 좌표계 $u_1=v_1, u_2=v_1+v_2, u_3=v_1+v_2+v_3$이 있다.
벡터 $w=[1, 2, 3]^T$를 $v$에 관한 식 $w_1$과 $u$에 관한 식 $w_2$두가지로 표현하라.

$v$좌표계는 우리가 아는 x, y, z 좌표계로 바로 $w_1=v_1+2v_2+3v_2$가 나온다.

앞에서 좌표계를 변환할때의 식 $u = Mv$를 적용하면, $M=\begin{pmatrix}1&0&0\\1&1&0\\1&1&1\end{pmatrix}$이 된다.

$w1$ 또한 벡터이므로 $w_2=(M^T)^{-1}w_1$로 전치역행렬을 하면 구할 수 있다.

Polygon

실제로 그래픽스에서는 면이 어떤식으로 존재할까?

점만 있는데 이를 연결하면 선이 되고, 이 선이 모여 면이 된다.

이러한 원리로 면이 모여 3D모델이 되고, 이것을 Polygon이라고 한다.
우리의 얼굴을 폴리곤으로 표현한 모습이다.

이러한 Polygon은 방향이 존재하는데, 이 방향은 2가지가 존재한다.

벡터의 외적으로 구한 면의 방향을 normal of the plane이라고 했는데 아래로 수직인지, 위로 수직인지가 나온다.

보통 이 방향은 오른손 법칙을 통해 해당방향을 outward-pointing이라고 한다.

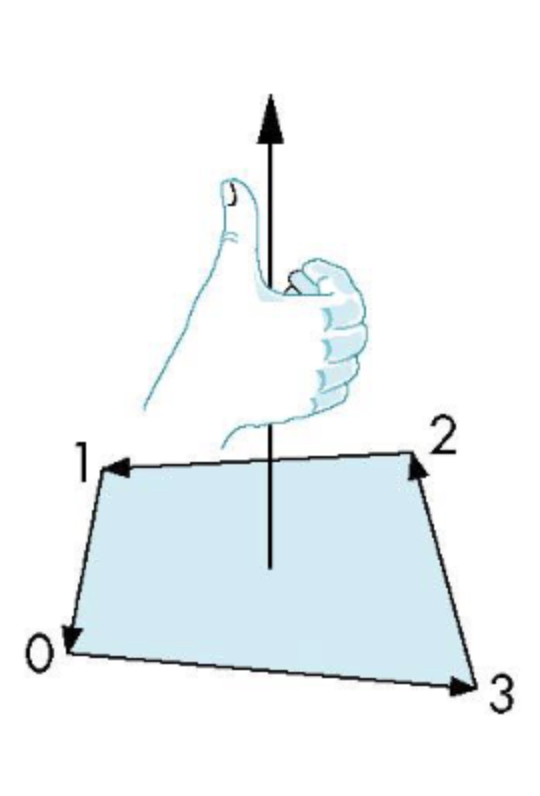
오른손으로 감싸서 위쪽이 outerward이며 반대는 inward이다.

Geometry vs Topology

• Geometry
  점들의 위치
• Topology:
  점과 선들의 관계

위 정의가 헷갈릴 수가 있다. 예를 들어 설명하면 단번에 이해가 될 것이다.

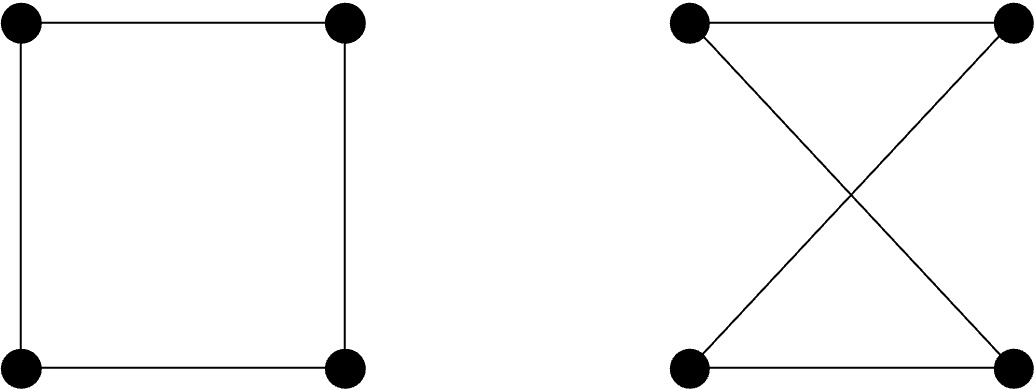
위 두 물체는 점들의 위치는 같아 Geometry는 같지만, Topology는 다른 것이다.

Vertex List

OpenGL 같은 그래픽 처리를 위한 API에서는 정점들을 리스트로 관리하여 폴리곤을 형성한다.

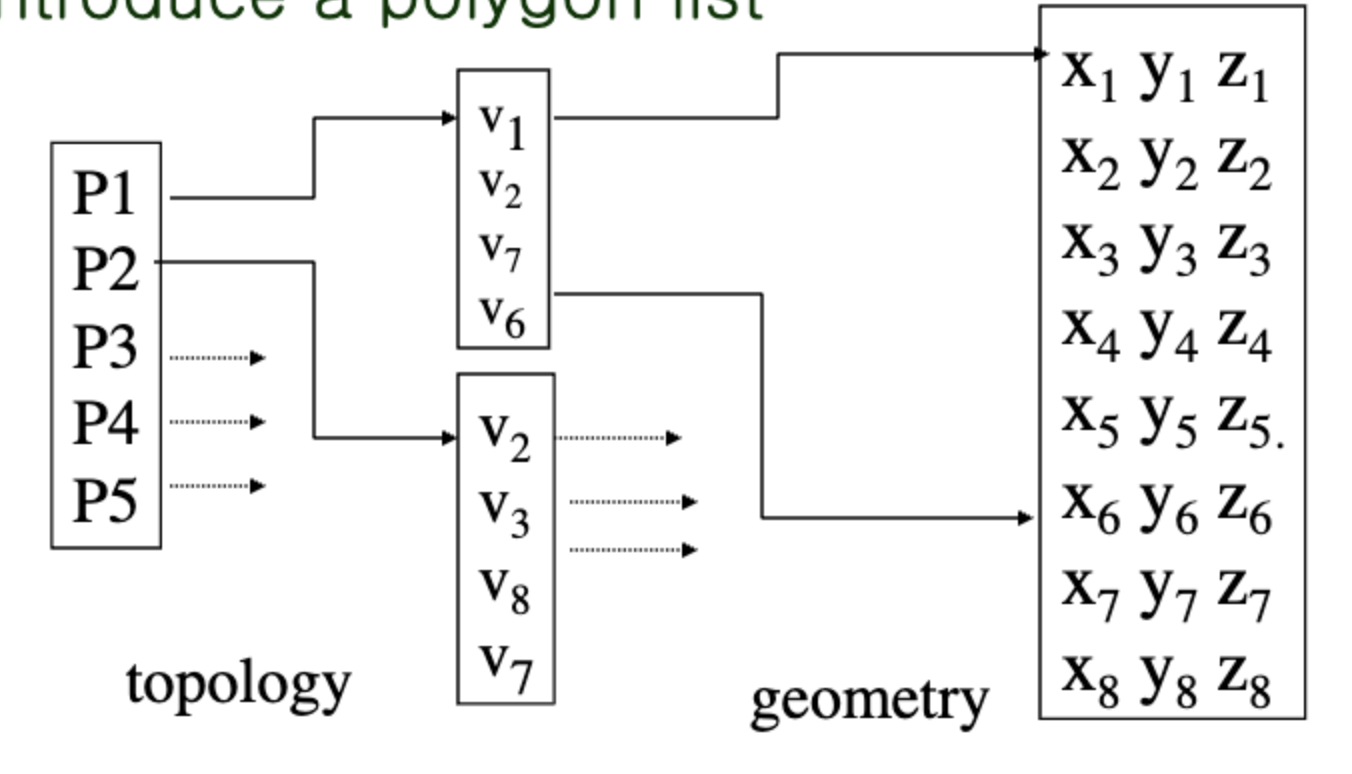
또한 아래의 정보를 포함하기도 한다

• 정점(Vertice)
• 색깔(Color)
• 면의 방향(Normal)
• 이미지 에셋(Texture)
  등