Transformation in 3D Space
이때까지 2D 세상에 대한 Transformation을 배웠다.
우리는 3D 공간에 살기에, 이 공간에서 어떻게 Transformation이 계산되는지를 알아보자.
Transformation
복습
어떠한 점이나 벡터를 새로운 점이나 벡터로 변환하는 것을 Transfomation이라고 한다.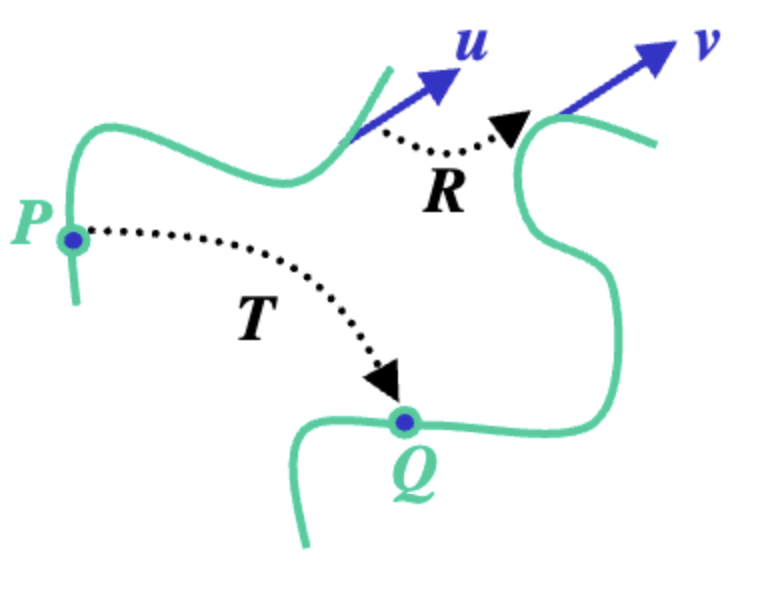
를 다시표현하면 로 된다.
왼쪽의 초록색 선을 오른쪽의 선으로 변환하는 함수인 는 transformation function이다.
Affine Transformation
변환은 선형적인 특성을 가지고 있기에 다음식을 만족한다.
곱하기로 분리가 가능한 성질을 homogeneity 더하기로 나누는 성질을 additivity이라고 한다.
또한 변환을 하고 변환을 한 결과 이 동일한 교환법칙도 성립하며, 이외에도 결합, 분배법칙이 성립한다.
또한 변환을 한 것을 되돌리는 변환도 존재한다.
homogenous coordinate
3D 공간에 있는 위치좌표를 2D인 디스플레이에 보여주어야하므로 homogeneous coordinate가 필요하다.
벡터는 으로, 점은 처럼 표시하며, 변환행렬은 로 표현한다.
Translation
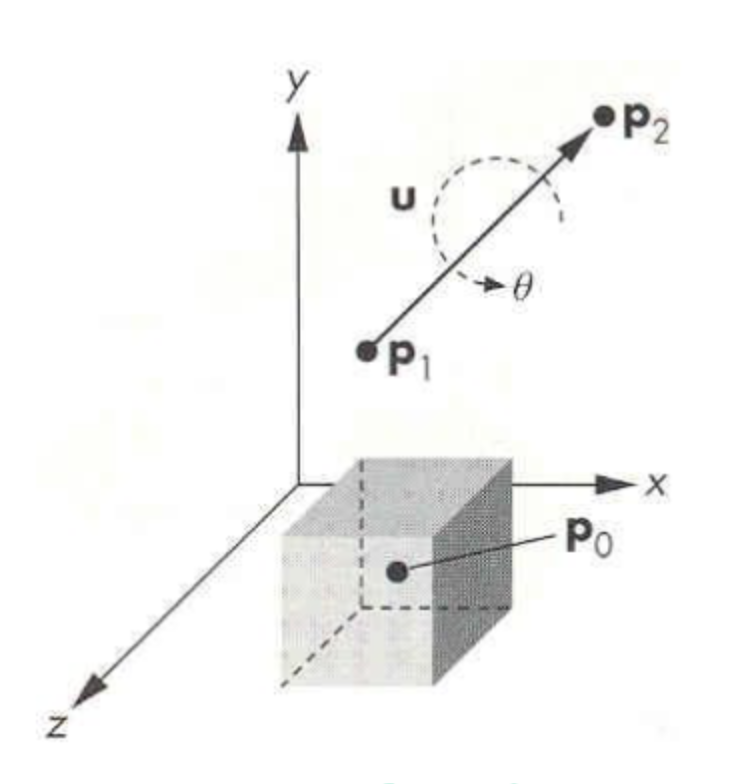
특정 벡터나 점을 어느 방향으로 이동시키는 변환이다.
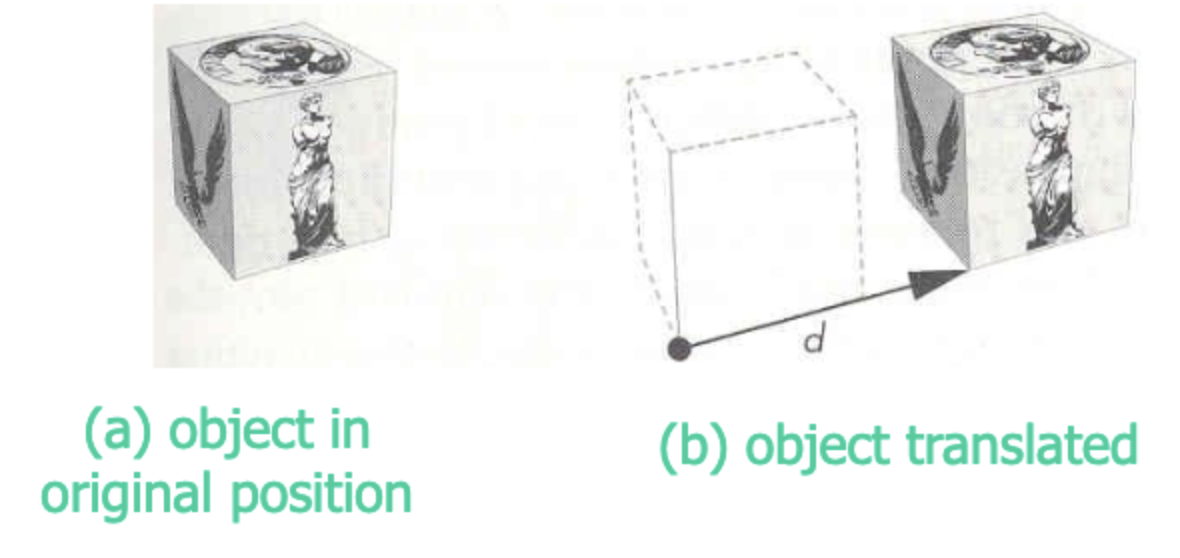
점 를 방향벡터 만큼 이동시켜 점 로 이동시켰을 때 다음을 만족한다.
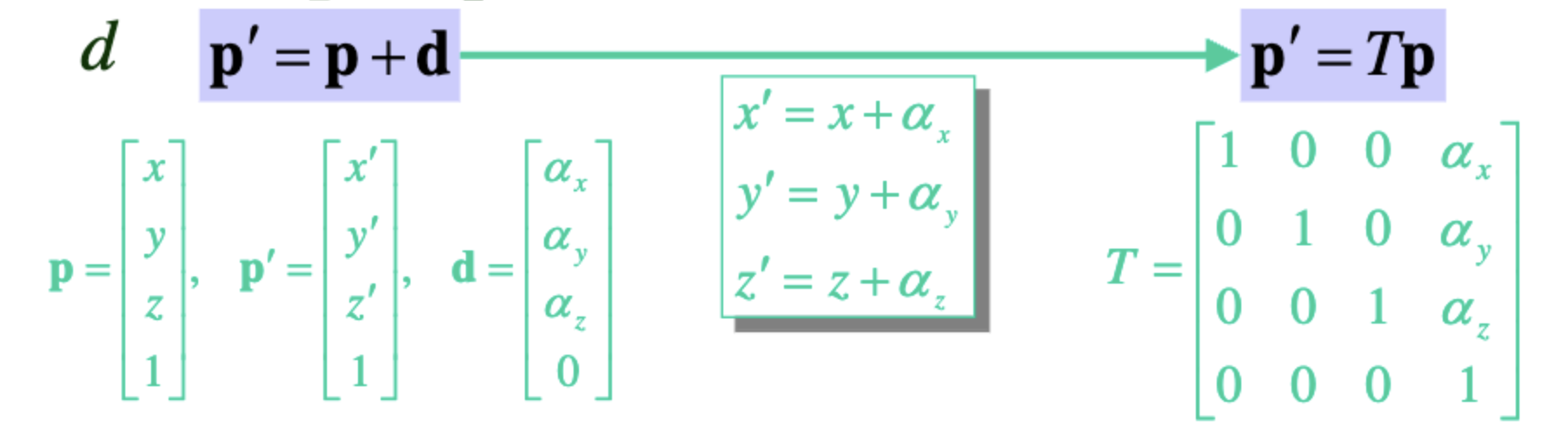
Scaling
특정 벡터나 점을 확대나 축소시키는 변환이다.
가로 세로 비율을 일정하게하면 uniform scaling,
그게 아니라면 nonuniform scaling이라고 한다.
x방향으로 배, y방향으로 배, z방향으로 배를 한 결과는 다음과 같다.
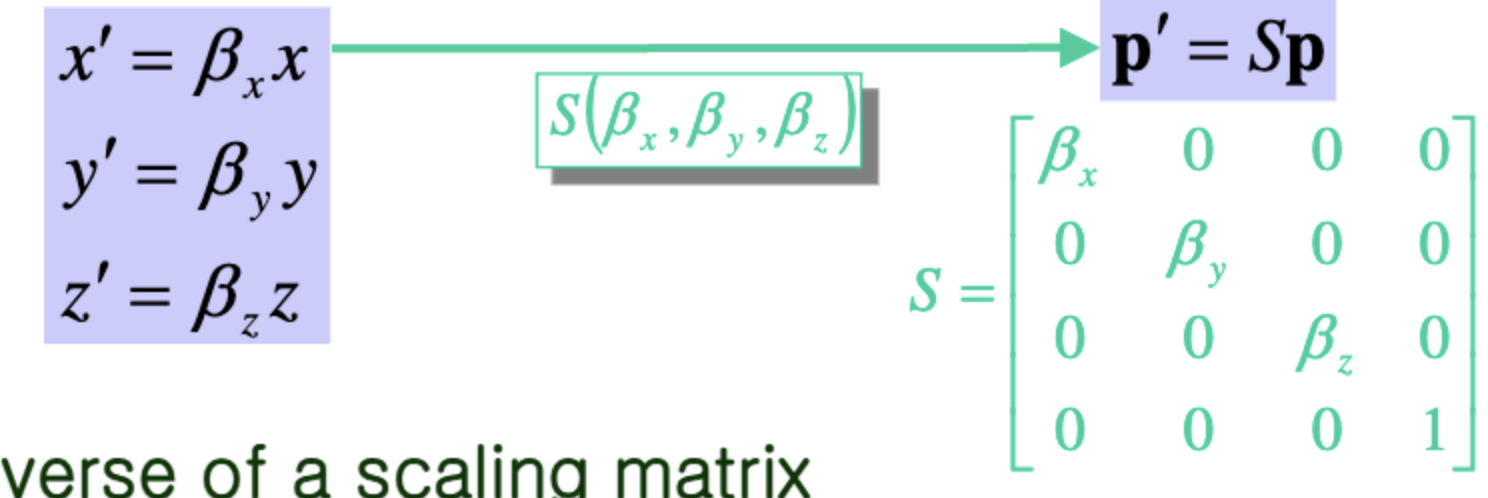
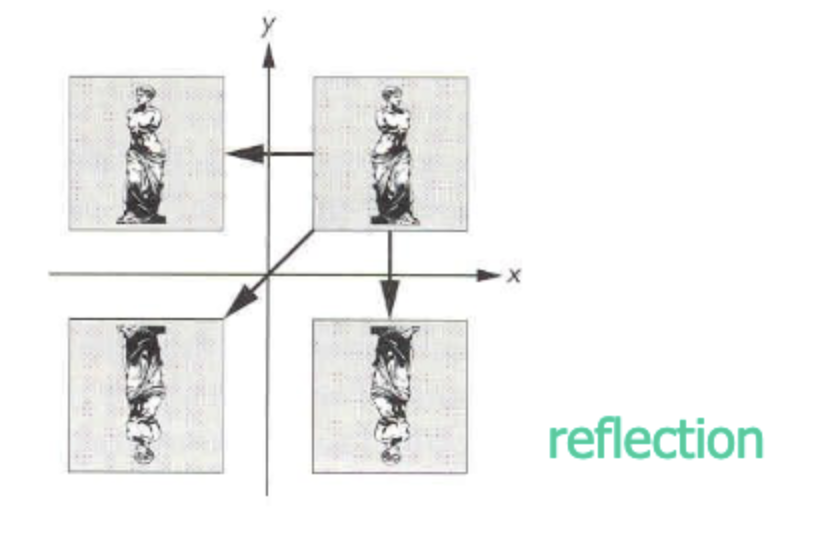
만약 음수배를 했다면?
폴리곤이 뒤집혀 보이는 reflection 현상이 일어난다.
Rotation
3D 모델이 회전하기 위해선 3가지 요소가 필요하다.
- 회전축
- 회전중심
- 회전각
그리고 회전각에 대한 변환식은 오일러 공식에 의해 다음을 만족한다.
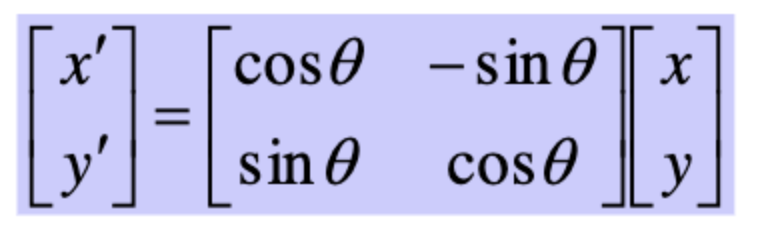
3차원에서는 그러면 어떻게 될까?
위의 수식은 2차원이다. 2차원에서는 z축의 개념이 없기에 x와 y값이 바뀐다.
즉, z축이 회전축이라면 z를 제외한 값들이 바뀐다는 의미이다.
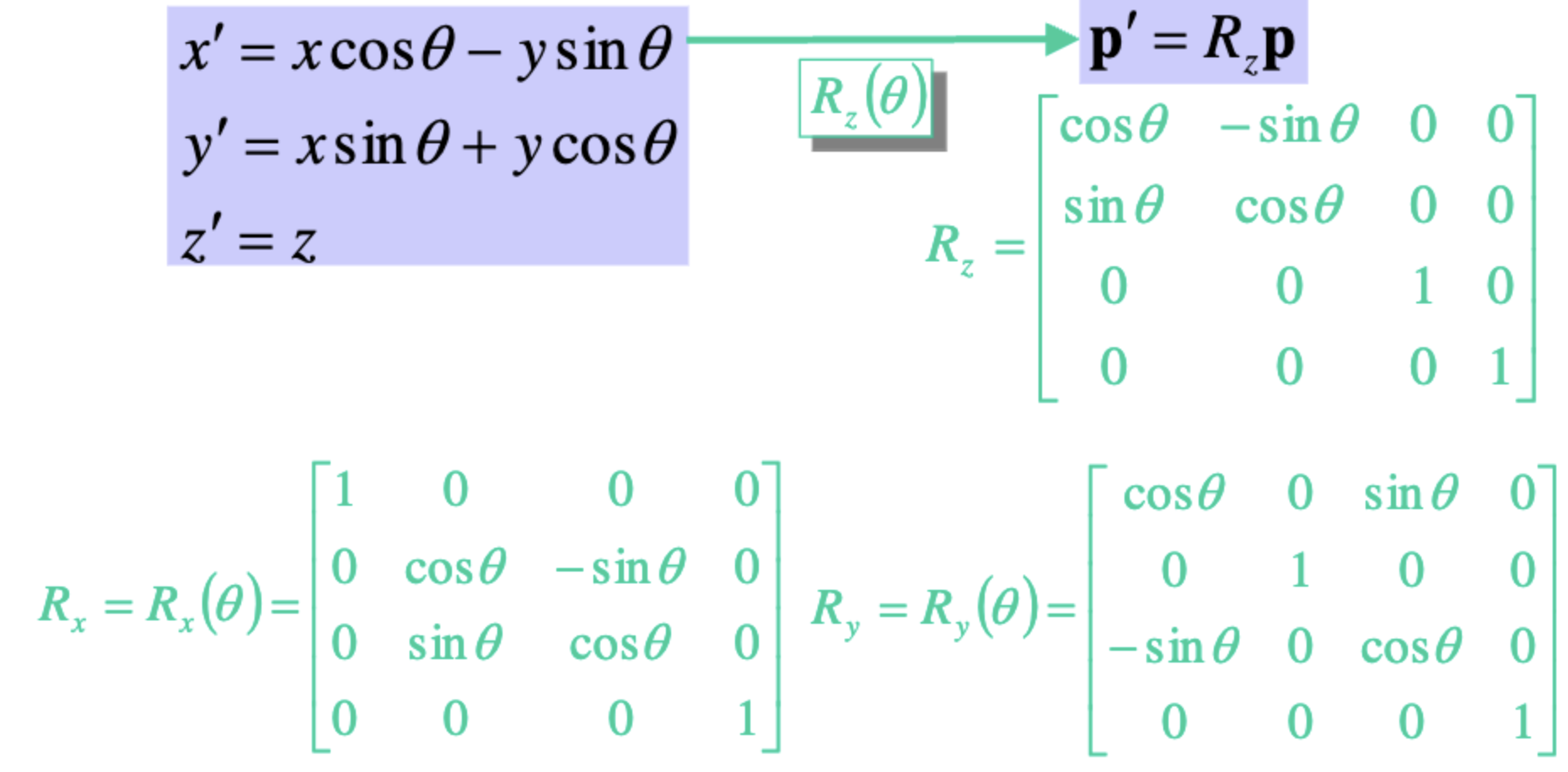
z축회전은 x와 y를, x축회전은 y와 z를, y축회전은 x와 z를, 변환시키는 것이다.
회전중심을 정해 연산하는 법
이때까지 배운 회전은 중심이 (0, 0)인 기준으로 회전하는 것이었다.
하지만, 회전중심이 (1, 1)이거나 (100, 100)이라면?
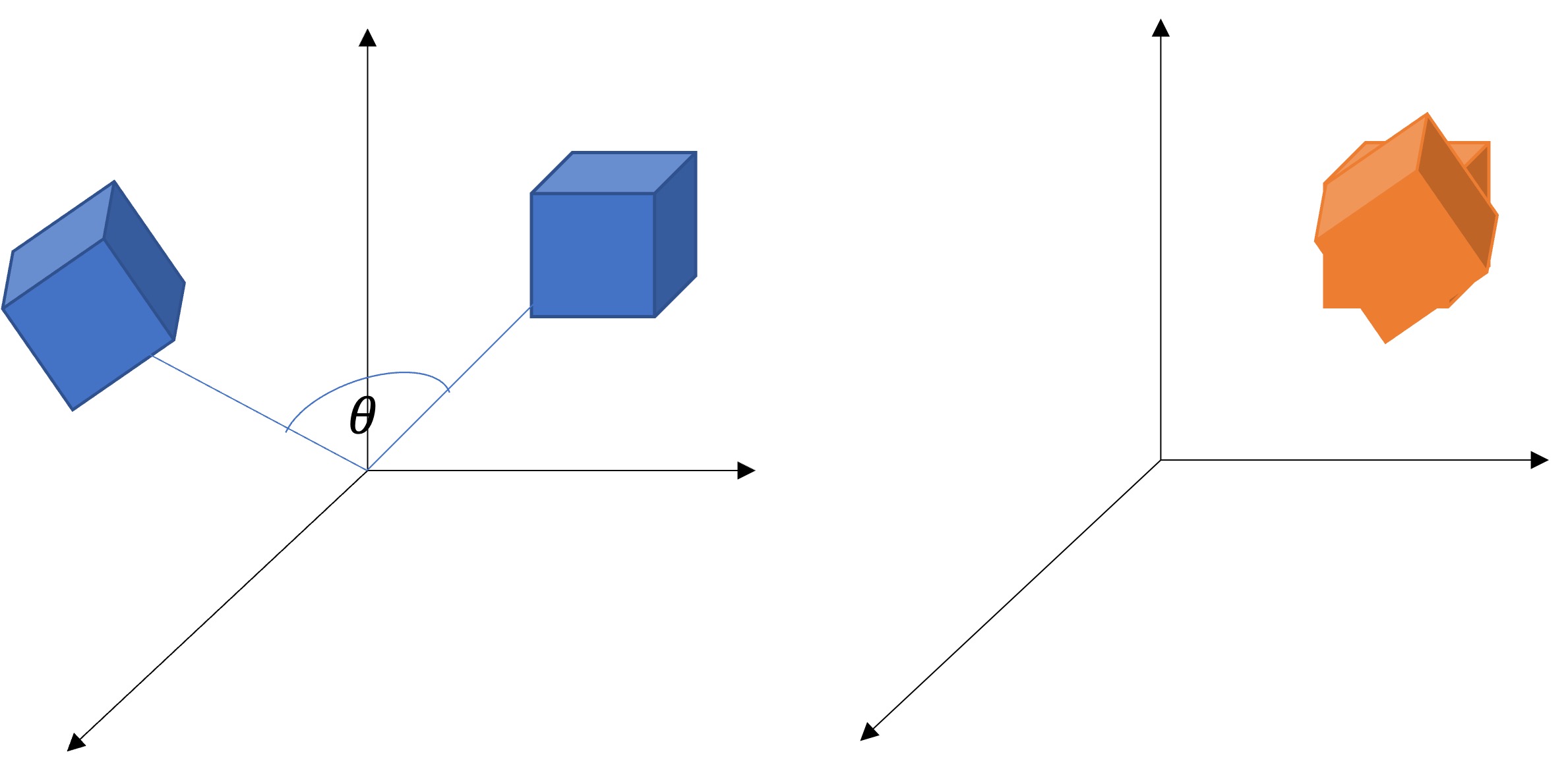
같은 회전각이지만 회전중심에 따라 결과가 달라질 수 있다.
그래서 다음의 Flow를 따라야한다.
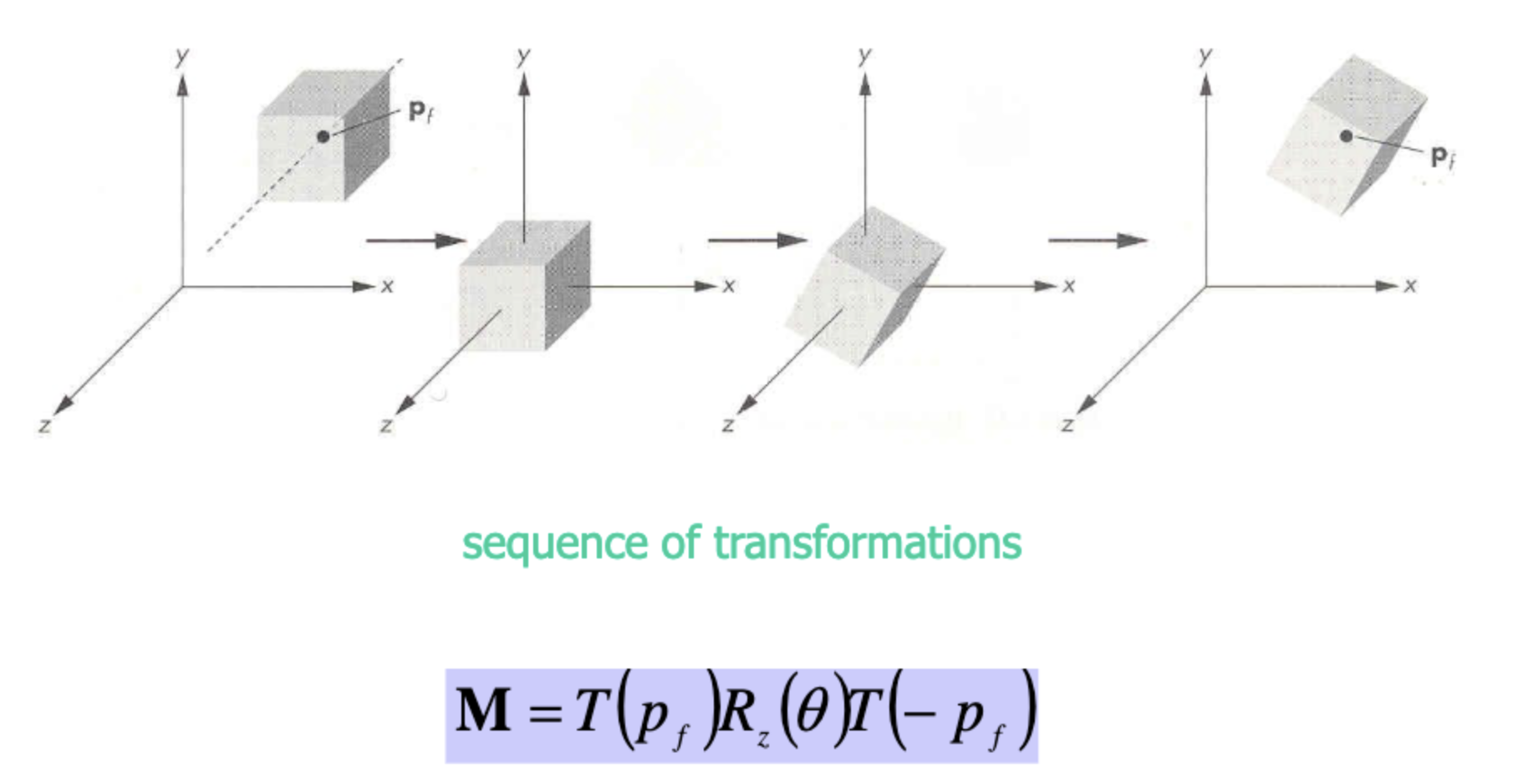
1. 회전중심을 원점으로 옮긴다.
2. 회전시킨다.
3. 회전중심을 다시 원래의 위치로 옮긴다.
이 결과를 행렬식으로 나타내면 다음과 같다.

Arbitrary Rotate
회전의 3요소가 다음과 같다고 하자.
- 회전축:
- 회전중심:
- 회전각:
이전의 회전축이 중심이 아닐 때는 먼저 Translate를 하고 돌린후 다시 복원한다고 하였다.
또한, 회전축 을 z축에 맞춰서 회전시키면 편할 것이다.
그래서 z축을 기준으로 맞추기 위해, x축, y축기준으로 회전시킨다.
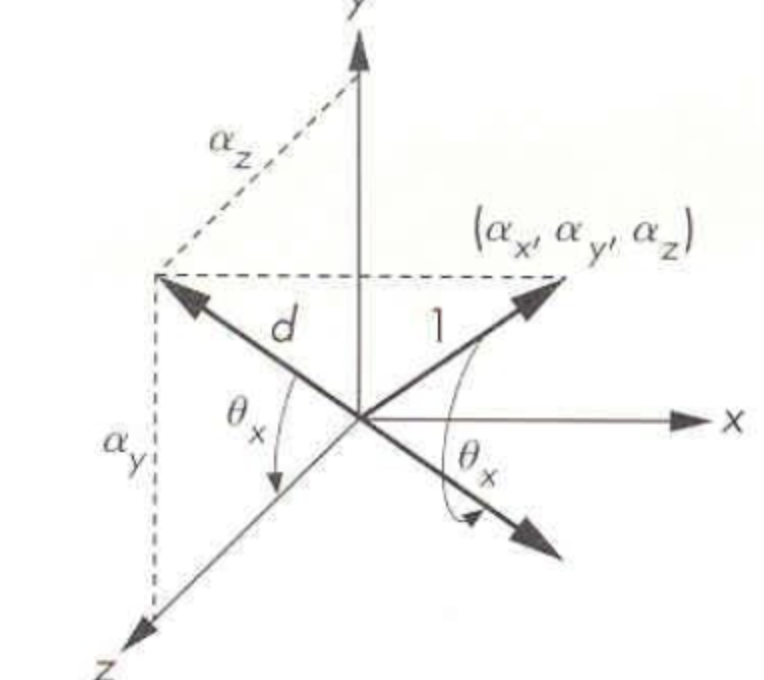
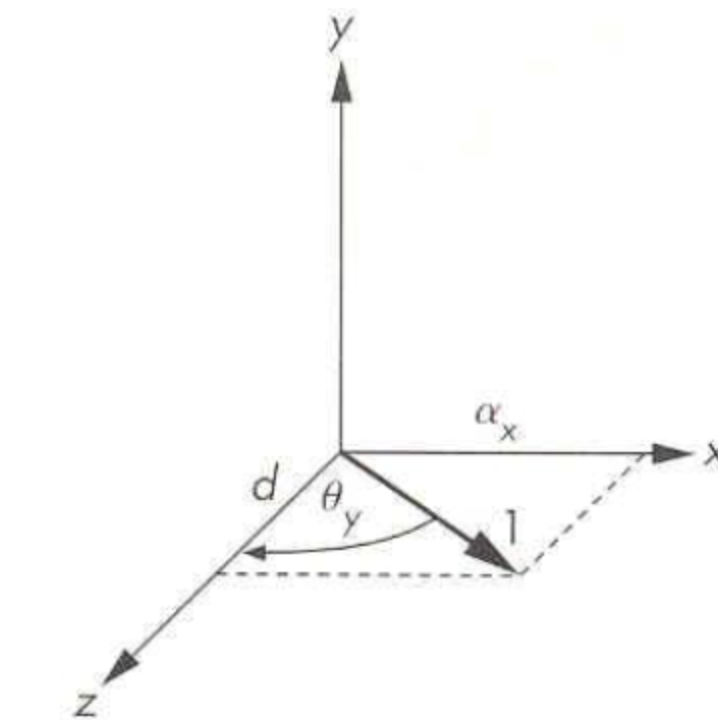
이렇게 기존의 회전축 을 z축과 평행하도록 맞췄다면, 회전각 만큼 돌린다.
이후 y축, x축으로 반대로 회전시켜 원본으로 돌리고, 이전에 회전중심을 위해 Translate했던 것을 다시 원상복귀 시킨다.
이 모든 과정을 정리하면 아래와 같다.
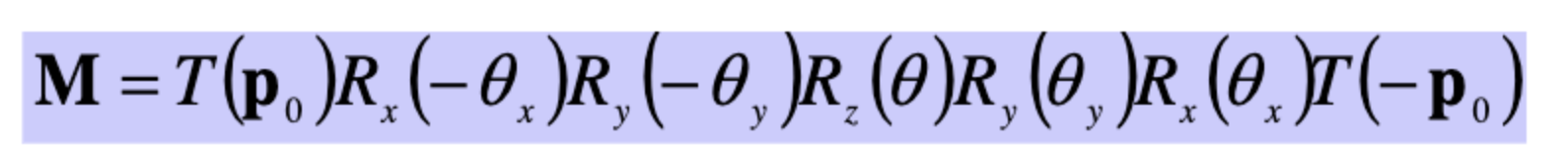
연산 순서
연산순서는 Scale -> Rotate -> Translate 순으로 하는게 편하다.
왜냐하면 이미 3D모델이 원점에 있을 때 Translate를 하고 Rotate를 하면,
회전중심이 바뀌어 전혀 다른 결과를 만들 수도 있기 때문이다.
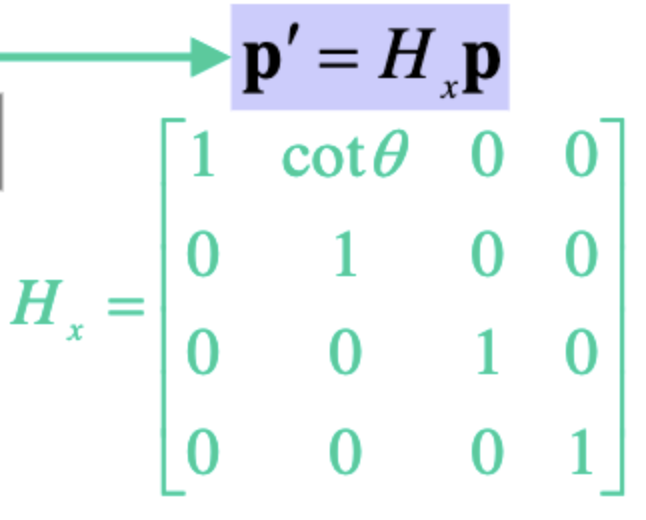
Shear
물체를 찌그러뜨리는 변환이다. 뭔가 쓸모 없어보이지만 중요하다.
추후 Oblique Projection할 때 사용하기도 한다.
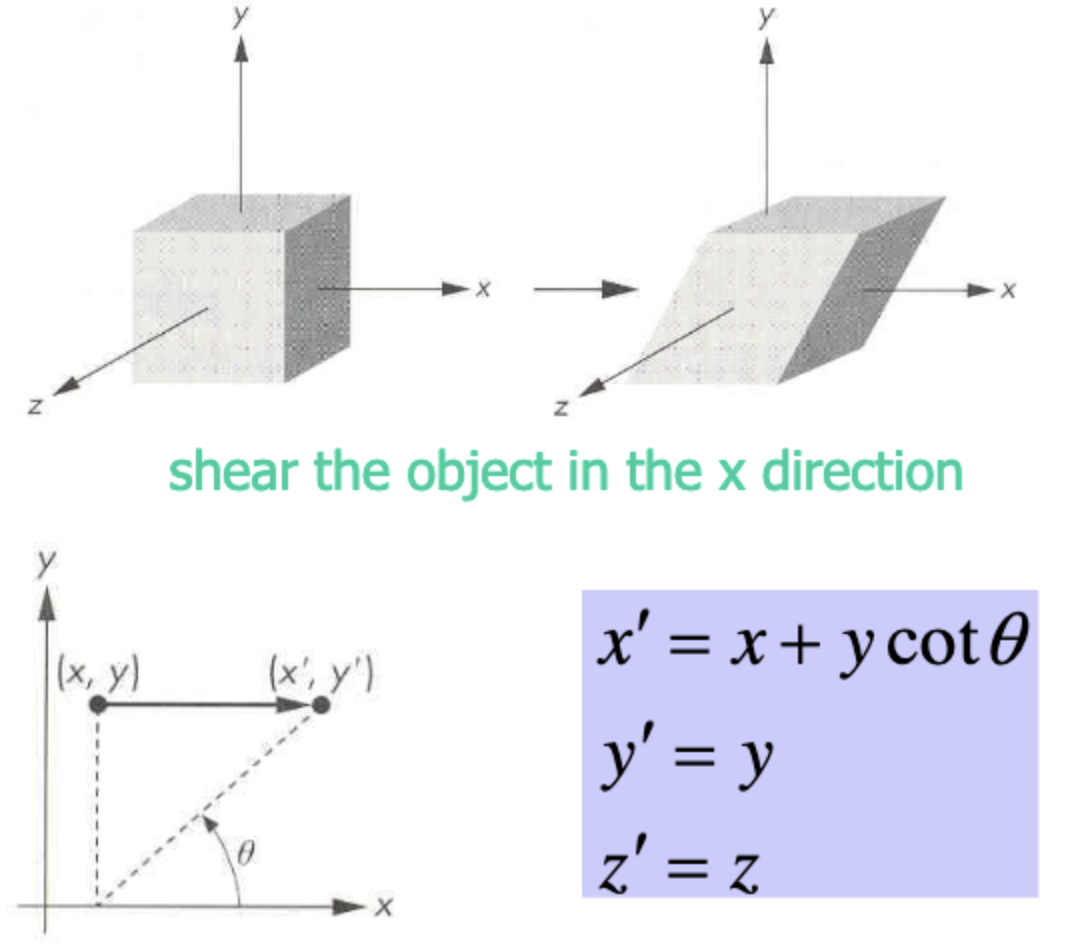
위의 방정식을 만족하기 위한 행렬식은 아래와 같다.