Viewings

• COP(Center of Projection) 점한곳에 모이는 방식
  
  점 하나에서 빛이 퍼져나가는 그 원근감 모시기할 때 쓰는 것
• DOP(Direction of Projection) 평행하게 점이아니라 일자로 빛이 퍼지는 방식
  
  그냥 원근법 모르겠고 납작하게 정사영시킨 그대로를 보여주는 것

다양한 Viewing

다양한 Viewing이 존재한다.

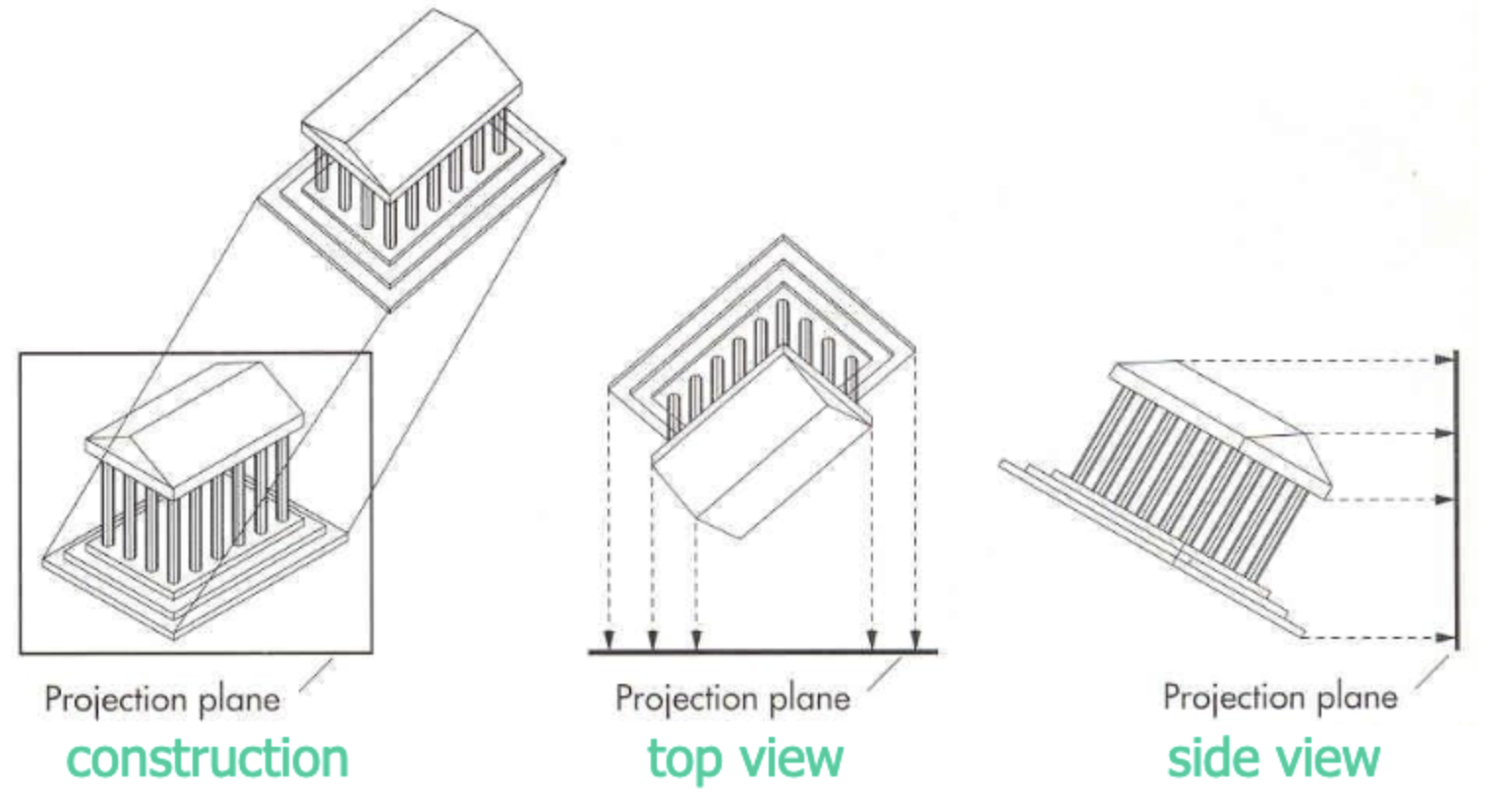
Orthographic Projections

모든 선들이 수직으로 표현되는 방식으로, 건물 전면도, 측면도 이런거라보면된다.

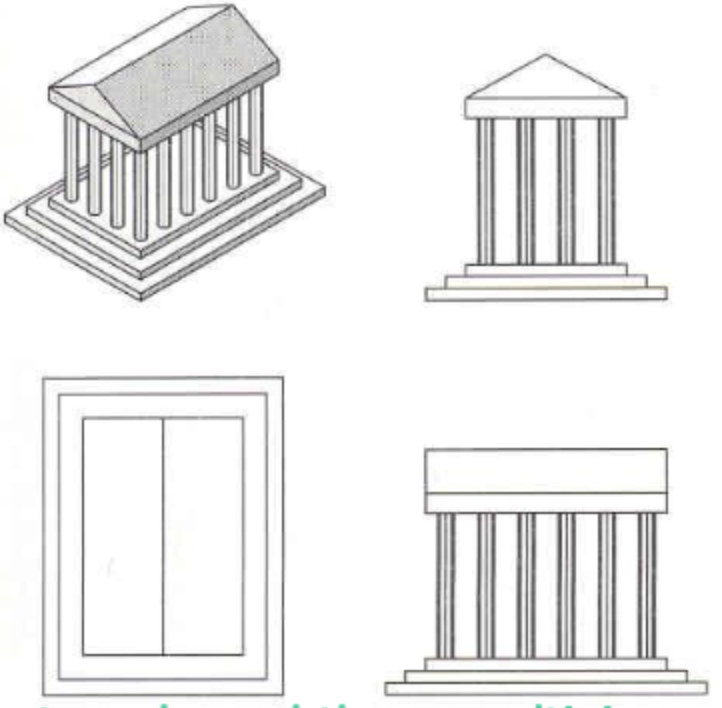
Axonometric Projections

Orthographic은 말그대로 모든 각을 수직으로 표현한다면, Axonometric은 수직이 아닌 것을 뜻한다.

이 안에는 크게 3가지로 나뉜다.

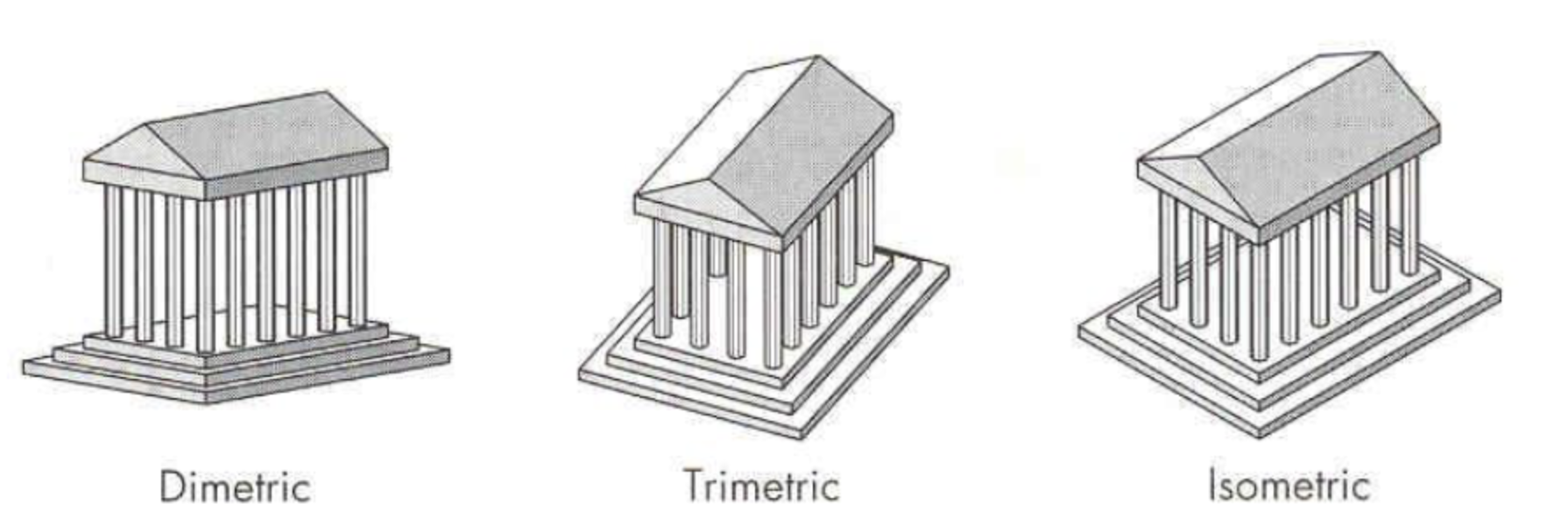
Diemetric: 각 2개만 똑같은 것
Trimetric: 각 3개가 모두 다른 것
Isometric: 각 3개가 모두 같은 것

뭔 소린지 이해가 안된다면 당신은 바보이다.

이해를 쉽게 하기위해 감히 내가 노트를 가져와 설명을 해보자면 다음과 같다.

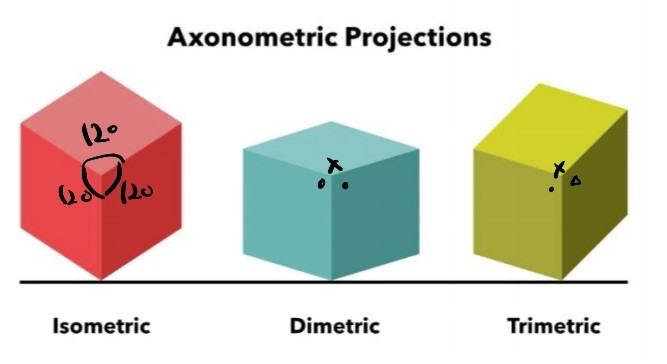
이거 보고도 이해안되면 흠..

Oblique Projections

미술 학원 좀 다녀봤다하면 선생님이 연필한자루 쥐어주고 데셍을 오지게 시킨다.

그때 5개의 큐브를 생성하는 능력을 배울 수 있다. 어떤 모습의 큐브냐면 이때 이것이다.

정면과 상부, 측면 총 3가지 면이 동시에 보이는 말도 안되는 현실에 아리에나이한 것을 투영하는 법이다.

저번 챕터에서 배운내용을 여따가 써먹을 수 있다. 바로 Shear이다.

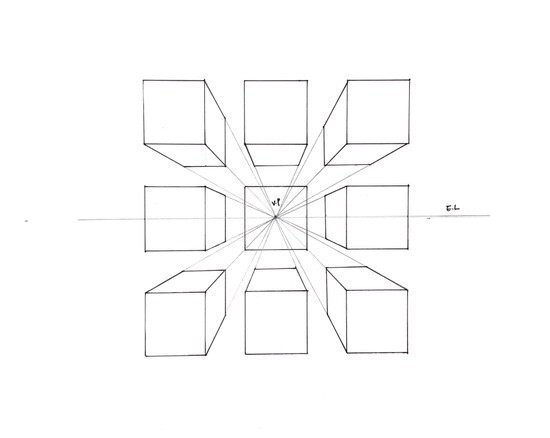
Perspective Projections

사실 위에서 배운건 전부 현실의 우리 눈으로는 목격할 수 없는 Projections이다.

빛은 우리의 눈으로 모이고, 멀리있는 건 작게 가까이있는건 크게 보이는게 인지상정.

이런 복잡한 Perspective에는 종류가 3가지 있다.

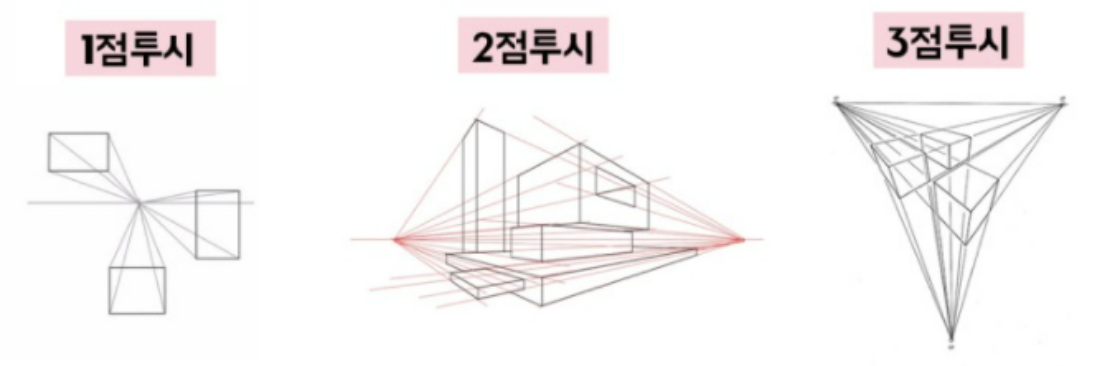
먼 것은 작아지다가 결국 0에 수렴하는 점이 있는데, 여기를 소실점이라고 한다.

이 점의 개수에 따라 원근감을 보다 쉽게 표현할 수 있다.