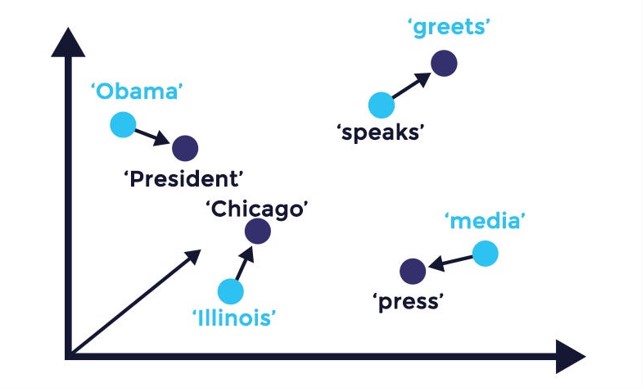
1. Definition of Word Embedding
NLP에서 단어를 기계가 이해할 수 있는 형태로 표현하기 위해서는, 단어 그 자체가 지닌 의미나 문맥 정보를 벡터 형태로 바꿀 필요가 있다. 이를 Word Embedding이라 한다. Word Embedding은 단어 사이의 의미적 유사도나 연관성을 유지하면서도, 기계학습 모델에서 다루기 적합한 고정 차원의 실수 벡터로 변환한다. 이러한 방식은 단어 하나하나가 지닌 중의적·복합적 특징들을 간결하게 압축하면서도, 단어 사이의 연관성도 유지시킨다.
1.1. Embedding이란?
수치화하기 어려운 객체(예: 단어, 문장, 이미지 등)를 고정 길이의 실수 벡터로 나타내는 과정을 Embedding이라 한다. 이 벡터는 각 차원에 특정 의미가 고정된 것이 아니라, 전체적으로 의미를 분산적으로 표현한다. 예를 들어, 이미지 처리는 픽셀을 입력으로 사용하지만, 자연어처리에서는 단어나 문장을 직접 숫자로 치환하기 어렵기 때문에 벡터화를 위한 임베딩 기법이 발달해 왔다.
이 과정에서 중요한 역할을 하는 것이 바로 feature extraction이다. 전통적인 NLP 접근에서는 단순히 단어의 존재 여부(또는 빈도) 같은 “Sparse Feature”를 사용했지만, 임베딩 기법을 도입함으로써 단어 간의 관계를 학습된 벡터 구조로 담을 수 있게 된다.
즉, 단순히 “문서에 단어 A가 있다”라는 이진 정보 수준을 넘어, 단어 A가 어떤 문맥에서 어떻게 사용되는지를 포함한 풍부한 의미 정보를 분산 표현 형태로 추출해낼 수 있다.
1.2. Word Embedding이란?
Word Embedding은 텍스트 상의 단어를 일정 차원의 실수 벡터로 매핑하는 기술적 방법을 일컫는다. Word2Vec, GloVe, FastText 등 다양한 알고리즘이 대표적인 예시다.
(이 알고리즘들에 대해서는 후속편에서 하나하나 세심하게 다룰 것이다!)
이들 방법은 보통 대규모 말뭉치를 기반으로 단어의 “분포적 특성(distributional characteristics)”을 학습한다.
예를 들어, 비슷한 맥락에서 자주 등장하는 단어들은 벡터 공간에서 서로 가까운 위치를 가지게 되고, 이는 즉 그 단어들이 서로 연관되어있을 확률이 높다는 것을 의미하게 된다.
이렇게 얻은 분산 벡터는 차원이 '수십 ~ 수백'에 불과하므로, 과거에 사용하던 One-hot 벡터('수만 ~ 수십만' 차원)에 비해 훨씬 효율적이다. 또한 모델이 단어의 맥락적 의미와 연관성을 학습하기 때문에, Text classification, Sentiment analysis 등의 다양한 NLP task에서 좋은 성능을 낸다.
2. Distributional Hypothesis
Distributional Hypothesis는 “단어의 의미는 해당 단어가 등장하는 주변 단어들(문맥)에 의해 결정된다”는 발상에서 시작된다.
고전적 표현으로는 “You shall know a word by the company it keeps”라고 불리며, 현대 자연어처리에서 단어 간 유사성을 추론할 때 가장 큰 이론적 기반이 된다.
이 아이디어에 따르면, 두 단어가 비슷한 맥락에서 자주 나타나면 그 단어들은 의미적으로도 유사하다고 볼 수 있다. 실제로 대규모 텍스트 말뭉치를 분석하여 “공동 등장 빈도(co-occurrence frequency)” 정보를 학습하면, 어떤 단어가 어떤 주제와 밀접하게 연결되는지를 직관적으로나 수식적으로나 파악할 수 있게 된다. 이때, 서로 유사한 단어들은 벡터 공간에서 서로 근접한 좌표를 갖게 된다.
2.1. Bag of Word
는 텍스트를 “단어들의 집합”으로만 바라보는 간단하면서도 직관적인 표현 방식이다. (이름부터가 "단어 가방"이다. 정말 단순하지만 그게 전부다!)
는 단어 순서나 구문 구조를 완전히 무시하고, 오직 어떤 단어가 몇 번 등장했는지만을 분석하는 것이다. 예를 들어, 말뭉치에서 자주 등장하는 단어를 바탕으로 단어장 를 만든 뒤, 특정 문서가 이 단어장에 있는 단어를 몇 번 포함하는지 계산하여 벡터로 나타낸다.
- 단어장
- 문서
- BoW 표현:
위 예시에서 는 문서 에 이 1회, 가 1회 등장하고, 는 전혀 등장하지 않는다는 것을 의미한다.
방법은 구현이 간단하고 계산 비용이 상대적으로 낮다. 단어 빈도를 세기만 하면 되므로, 텍스트 분류나 감성 분석 같은 작업의 기초 단계로도 자주 활용된다. 그러나 단어 순서나 문맥 정보가 전혀 고려되지 않기 때문에, 과 가 실제로 어떤 구문적 역할로 사용되었는지, 또는 어떤 문맥적 의미로 등장했는지는 BoW 벡터만으로는 알 수 없다. 결과적으로 는 직관적이며 단순하지만, 순서·의미 맥락 상호작용을 놓친다는 명확한 한계를 가진다.
2.2. TF-IDF
(Term Frequency – Inverse Document Frequency)는 접근의 확장판으로, 문서 전반에서 자주 등장하면서도 전체 말뭉치에서는 흔치 않은 단어를 더 중요한 단어로 가중치를 높게 부여하는 기법이다. 이를 두 단계로 나누어 살펴볼 수 있다.
2.2.1. TF(Term Frequency)
특정 문서 에서 단어 가 몇 번 등장했는지를 나타내며, 일반적으로 단순 빈도 를 의미한다. 그러나 실제 구현에서는 등을 적용한 변형 TF를 쓰기도 한다:
2.2.2. IDF(Inverse Document Frequency)
단어 가 전체 말뭉치(총 문서 수 ) 중 몇 개의 문서 ( ) 에서 등장하는지를 나타내며, 흔치 않은 단어일수록 높아진다. 일반적인 형태는 다음과 같다:
-> 가 작으면, 즉 매우 적은 문서에만 등장한다면 그만큼 값이 커져 해당 단어가 귀중한 정보로 취급된다.
결과적으로 와 를 곱하여,
공식을 통해 문서 내 단어 의 중요도를 산출한다.
예를 들어, 어떤 단어가 특정 문서에서는 매우 빈번하게 보이지만 다른 문서에서는 거의 등장하지 않는다면, 아마도 그 단어는 해당 문서에서 매우 중요한 특징일 것이다.
는 단순히 빈도를 세는 보다 세밀한 가중치 조정이 가능하므로, 정보 검색이나 텍스트 분류 등에서 흔히 사용된다. 다만 역시 단어 순서나 문맥적 의미는 제대로 반영하지 못하므로, 독립된 단어 수준에서 문서를 요약하는 데 그친다는 점에는 변함이 없다.
2.3. Document-Term Matrix
는 여러 문서와 단어 간의 등장 빈도를 “행렬” 형태로 표현한 것이다. 즉, 각 문서는 행(Row), 각 단어는 열(Column)에 해당하며, 각 셀에 해당 단어가 문서 내에서 몇 번 등장했는지 또는 값이 들어간다. 예를 들어 다음과 같이 구성할 수 있다.
| apple | banana | car | |
|---|---|---|---|
| Doc1 | 1 | 2 | 0 |
| Doc2 | 0 | 1 | 3 |
위 표에서 셀에는 1이, 셀에는 2가 기록된다. 이는 에 이 1회, 가 2회 등장했음을 의미한다. 비슷한 방식으로 가중치를 적용하면, 보다 좀 더 세밀하게 문서를 나타내는 을 얻을 수 있다.
여러 문서 정보를 한꺼번에 행렬로 관리하므로, 고차원 벡터 연산을 사용한 통계적 기법(예: 차원 축소, 군집화 등) 수행이 용이해지고, 단어별 중요도를 반영할 수 있다는 장점이 있지만, 여전히 단어 순서나 구문 정보를 전혀 포함하지 않고, 과 가 실제로 어떤 맥락에서 함께 쓰였는지, 와 가 어떻게 연결되어 있는지는 벡터 차원에서 직접적으로 알 수 없다는 단점이 여전히 존재한다. 또한 문서 수와 단어 수가 매우 클 경우 행렬의 차원이 기하급수적으로 커지게 되는 문제도 존재한다.
이는 BoW 기반 표현의 본질적 한계이기도 하다. 반면 Word Embedding 기법은 단어 간의 상호관계와 맥락까지 파악한 분산 표현(distributed representation)을 구축함으로써, 단어 순서, 인접성, 의미적 유사도 등을 포착해내려 한다는 점에서 DTM 접근과 대조적이다.
3. Vector Similarity
Word Embedding으로 단어를 벡터로 표현하면, 단어 간 유사도 혹은 단어간의 관념적 거리를 간단히 수치화할 수 있다. 지금부터는 Embedding Vector(물론 일반 Vector에도 적용 가능하다) 사이의 유사도와 거리를 측정할 때 자주 쓰이는 기법을 살펴보겠다.
3.1. Cosine Similarity
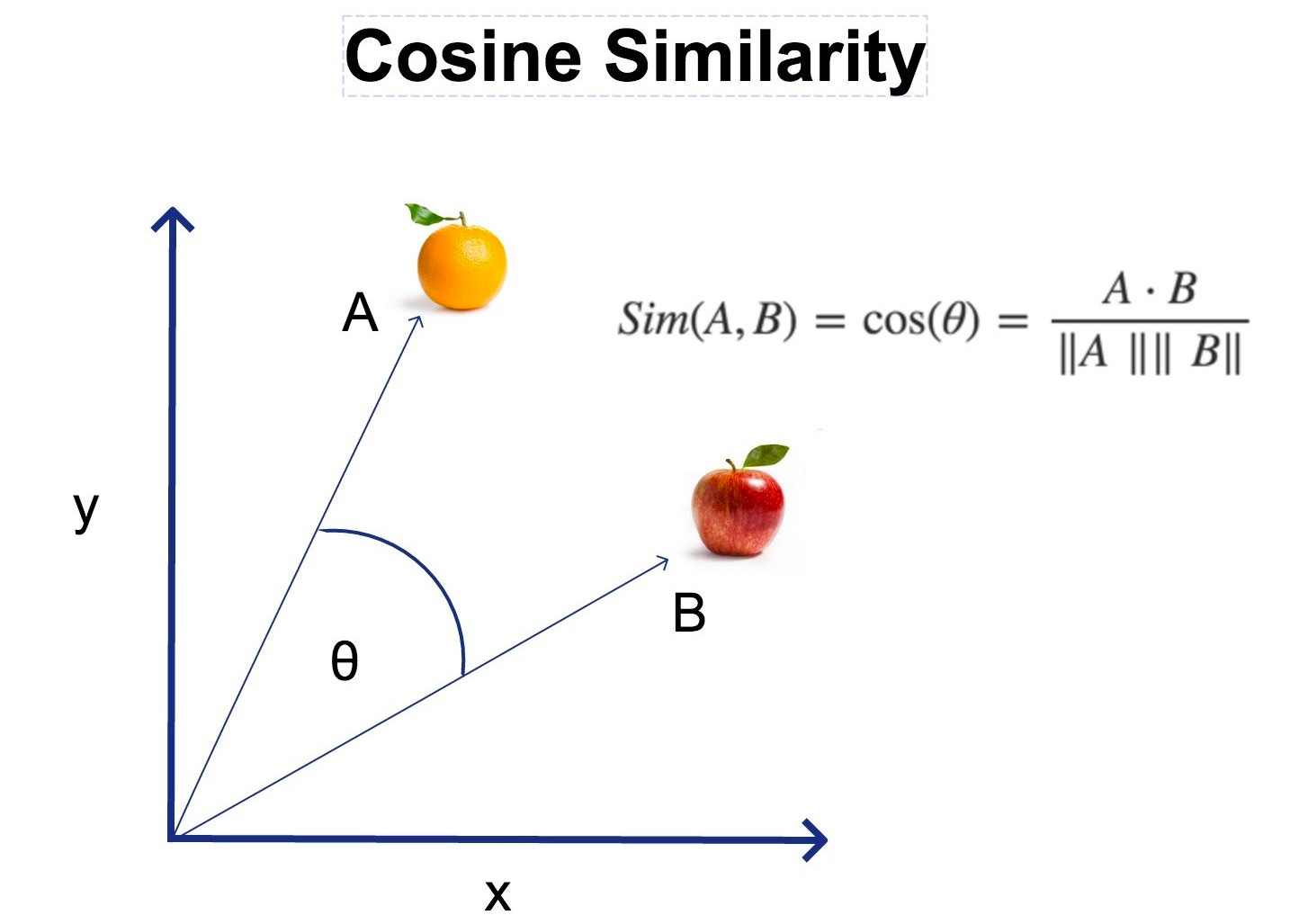
가장 흔히 쓰이는 벡터 유사도 중 하나가 Cosine Similarity다. 두 벡터 와 가 있을 때, Cosine Similarity는 다음과 같이 정의된다.
-
(내적),
-
(벡터의 크기).
Cosine Similarity는 주로 “두 벡터가 얼마나 방향이 유사한가” 에 초점을 맞추기 때문에, 벡터 길이 차이에는 비교적 둔감한 편이다. Word Embedding에서는 벡터의 절대 길이보다는 방향적 유사성이 단어의 의미를 더 잘 반영하기 때문에 Cosine Similarity가 널리 사용된다.
Cosine Similarity가 가장 흔한 방법이지만, 이 외에 다른 distance 산출 방법들도 간단하게 살펴보자.
3.2. Euclidean distance
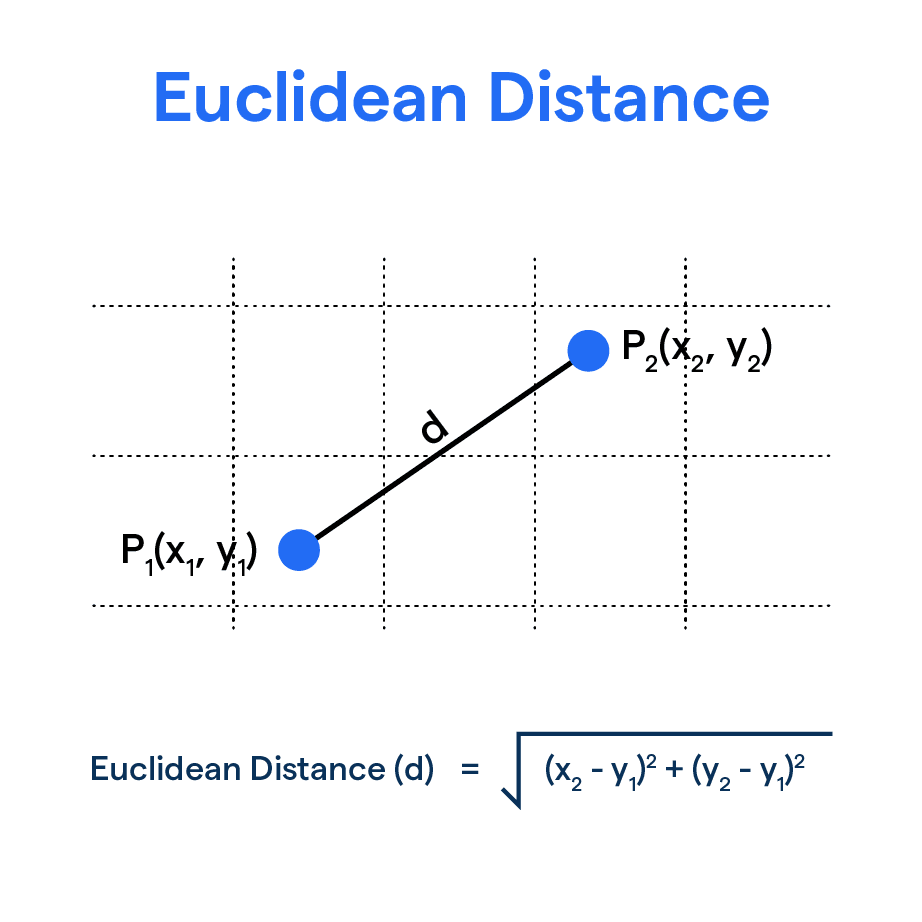
Euclidean distance는 기하학적으로 두 점 사이의 “직선 거리”를 나타낸다. 두 벡터 와 사이의 Euclidean distance는 다음과 같이 정의된다.
이 거리는 벡터의 전체적 크기와 위치 관계를 고려하므로, 원점에서의 거리(노름)도 함께 영향받게 된다. Word Embedding 같이 “방향 중심” 분석이 중요한 경우에는 Cosine Similarity를 더 선호하기도 하지만, “실제 공간적 거리”라는 개념이 필요한 특수한 상황에서는 Euclidean distance를 사용할 수 있다.
3.3. Jaccard Similarity
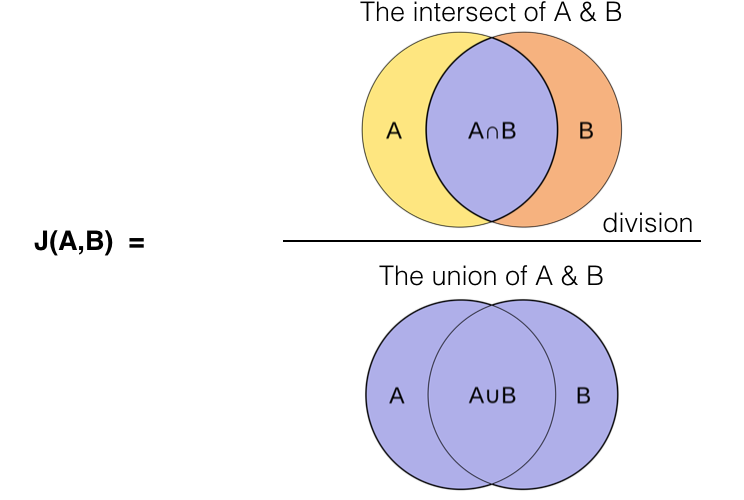
Jaccard similarity는 주로 집합 간 유사도를 측정할 때 사용된다. 두 집합 와 가 있을 때,
벡터를 이진(0/1) 형태로 해석할 수 있거나, 혹은 특정 임곗값을 기준으로 “활성화된 특성”을 집합처럼 볼 수 있을 때 적용 가능하다. 예를 들어, 텍스트에서 “단어가 등장했다”를 1, “등장하지 않았다”를 0으로 보고, 여러 문서를 이진 벡터로 표현한 뒤 Jaccard similarity를 구할 수 있다.
3.4. Hamming distance & Levenshtein Distance
이 둘은 엄밀히 말하면 벡터간의 유사도를 구하는데에는 윗 방법들 만큼 자주 쓰이지도 않고, main stream도 아니다. (오히려 자료구조 / 알고리즘 수업의 Dynamic Programming에 더 자주 등장한다.) 하지만 벡터간의 거리를 구하는 방법이며 embedding에도 종종사용되기에 알아 둘 필요는 있다.
3.4.1. Hamming distance
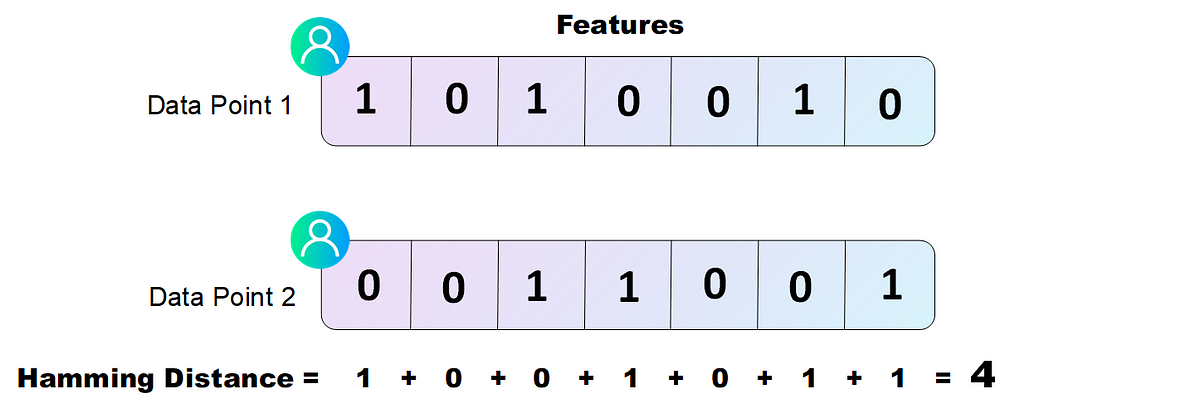
Hamming distance는 두 벡터(=문자열)에서 대응되는 위치가 다른 항목의 개수를 센다. 예를 들어, 다음과 같은 두 이진 벡터가 있다고 하자.
Hamming distance는
(서로 다른 위치가 2개이므로)
3.4.2. Levenshtein distance

문자열 편집 거리로도 불리며, 하나의 문자열을 다른 문자열로 바꾸는 데 필요한 삽입, 삭제, 치환 연산 횟수의 최소값이다.
예를 들어, 을 으로 바꾸기 위해서는 한 글자 치환이 필요하므로 거리는 이다.
앞서 언급했듯, 단어 임베딩 자체와는 조금 거리가 있지만, 텍스트 상에서 두 단어(혹은 두 문장)의 문자 차이를 직접 계산하고자 할 때 사용된다.
4. Reference
[1] 맞춤형 추천 알고리즘의 비밀: 벡터 유사도 (Vector Similarity)
[2] Hamming distance vs Levenshtein Distance
[3] 자연어처리 - 26 (Bag of words)
[4] TF-IDF 개념 및 계산 방법
[5] DTM(Document-Term Matrix, 문서 단어 행렬)