RL(2) - Markov Decision Process,MDP

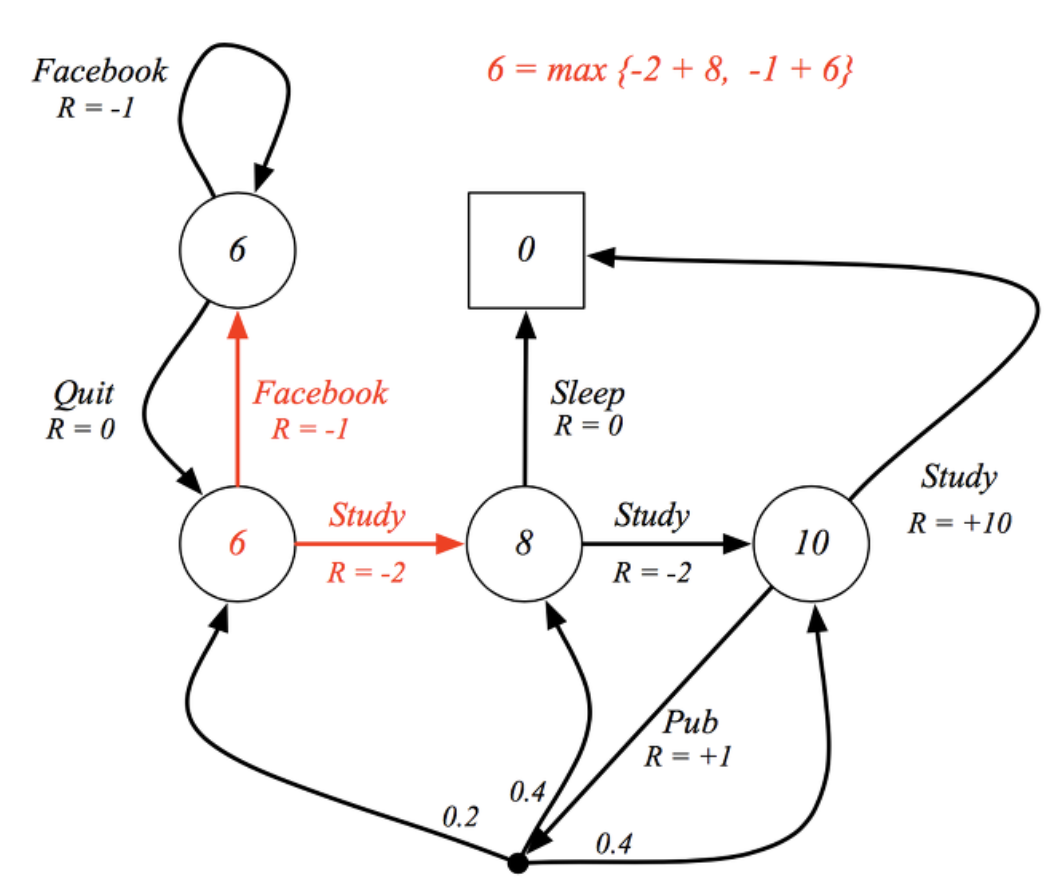
Markov Decision Process, MDP

Markov Decision Process는 기존 Markov Reward Process에 Action을 추가한 것이다.

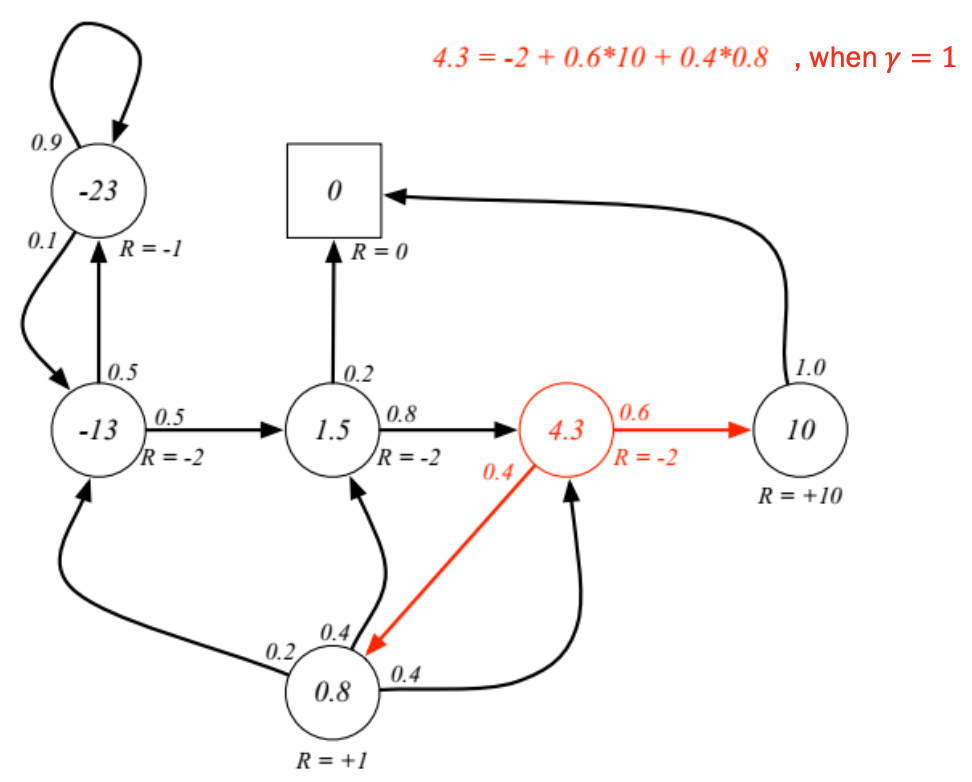
다음의 그림은 Markov Reward Process의 그림에 해당하는 것인데, C3에서 Sleep의 Reward을 받을 확률과, Pub의 reward를 받을 확률이 곱해지기만 하였다.

Markov Dicision Process에서는 다음과 같이 A라는 변수가 추가되게 된다. 이는 Action을 의미하며, $P_{ss'}^a = P[S_{t+1} = s' | S_t = s, A_t=a]$라는 기호를 바탕으로 각각의 action을 취할 policy를 계산할 수 있다.
또한 취한 action에 따라 Reward값이 달라지기에 $R_s^a = E[R_{t+1}|S_t = s, A_t=a]$를 이용하여 Reward값을 계산할 수 있다.

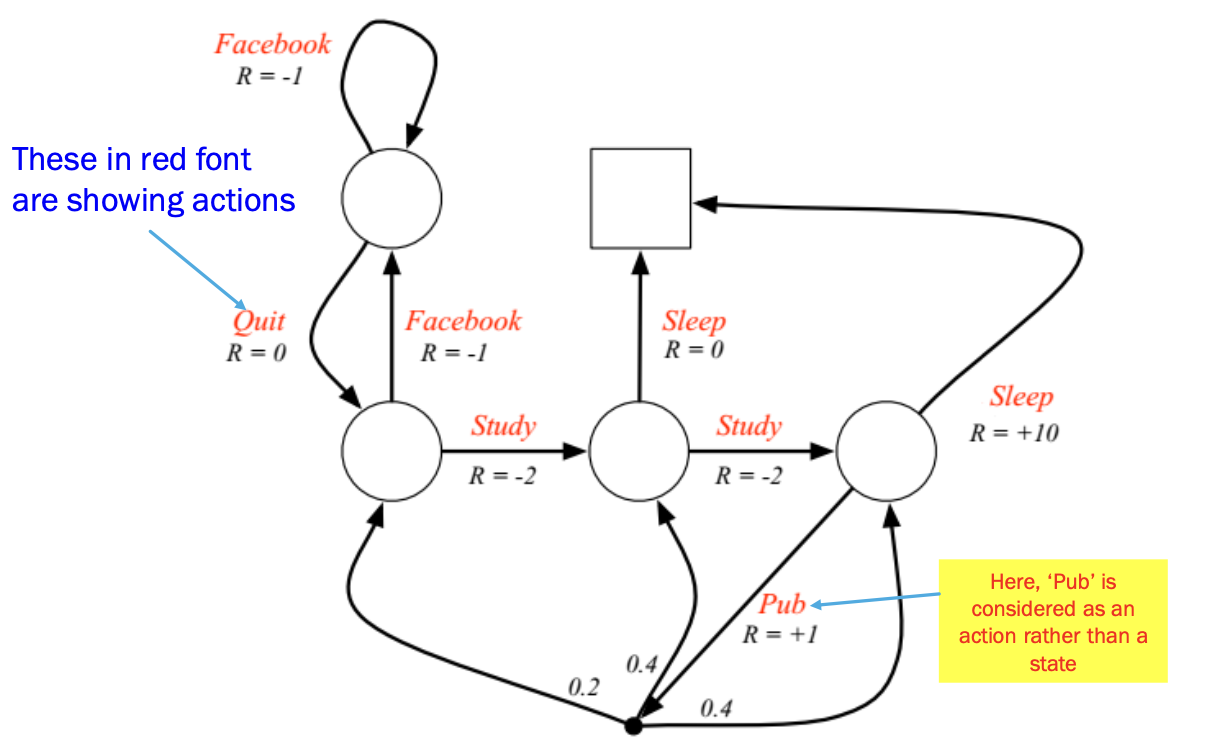
다음과 같이 Pub으로 가는 action을 취했을때 확정적으로 다음 state가 결정되는 것이 아닌, Probablity에 의해 다음 state가 결정된다.

Policies

policy는 앞에서 설명했던 것과 동일하게, 현재 state에 대해서 특정한 action을 취할 확률을 나타낸다. 기호로는 $\pi$를 이용하여 나타낸다.

MDP의 Policy는 현재 state값에 의해서만 특정한 action을 취할 확률이 결정되기에, 이전 timestep에 대해서는 독립적이다라고 얘기할 수 있다. (=stationary하다) 또한 시간에 따라서 해당 policy의 확률은 변하지 않는다.

Value Function

각각의 Policy $\pi$에 대해서 Value function을 새롭게 정의할 수 있다.

먼저 위의 $v_{\pi}(s)=E_{\pi}[G_t|S_t=s]$의 의미부터 먼저 살펴보면 다음과 같다.
해당 식은 state에 값의 return들의 Expectaion을 의미한다.
즉 해당 state에서 해당 $\pi$라는 policy를 취했을때 기대되는 미래 보상들의 평균이라고 생각 할 수 있다.

현재 상태에서 해당 policy를 취했을 때 얼마나 가치있고 좋은지를 따진다.

밑의 $q_{\pi}(s,a) = E_{\pi}[G_t|S_t=s,A_t=a]$의 의미를 살펴보자.
아까 구한 $v_{\pi}(s)$의 경우 모든 action들에 대하여 해당 policy의 return값의 평균이였던 반면, $q_{\pi}(s,a)$는 해당 policy에서 특정한 action에 대해서 얼마나 가치 있고 좋은지를 따지는 과정이다.

다음 value function은 Bellman Equation으로 표현할 수 있다.
앞의 식과 크게 다른 것이 아닌, $S_{t+1}$의 value function을 $\pi$policy를 가지는 value function으로 대체한 것 뿐이다.
$q$ function또한 동일한 것을 알 수 있다.

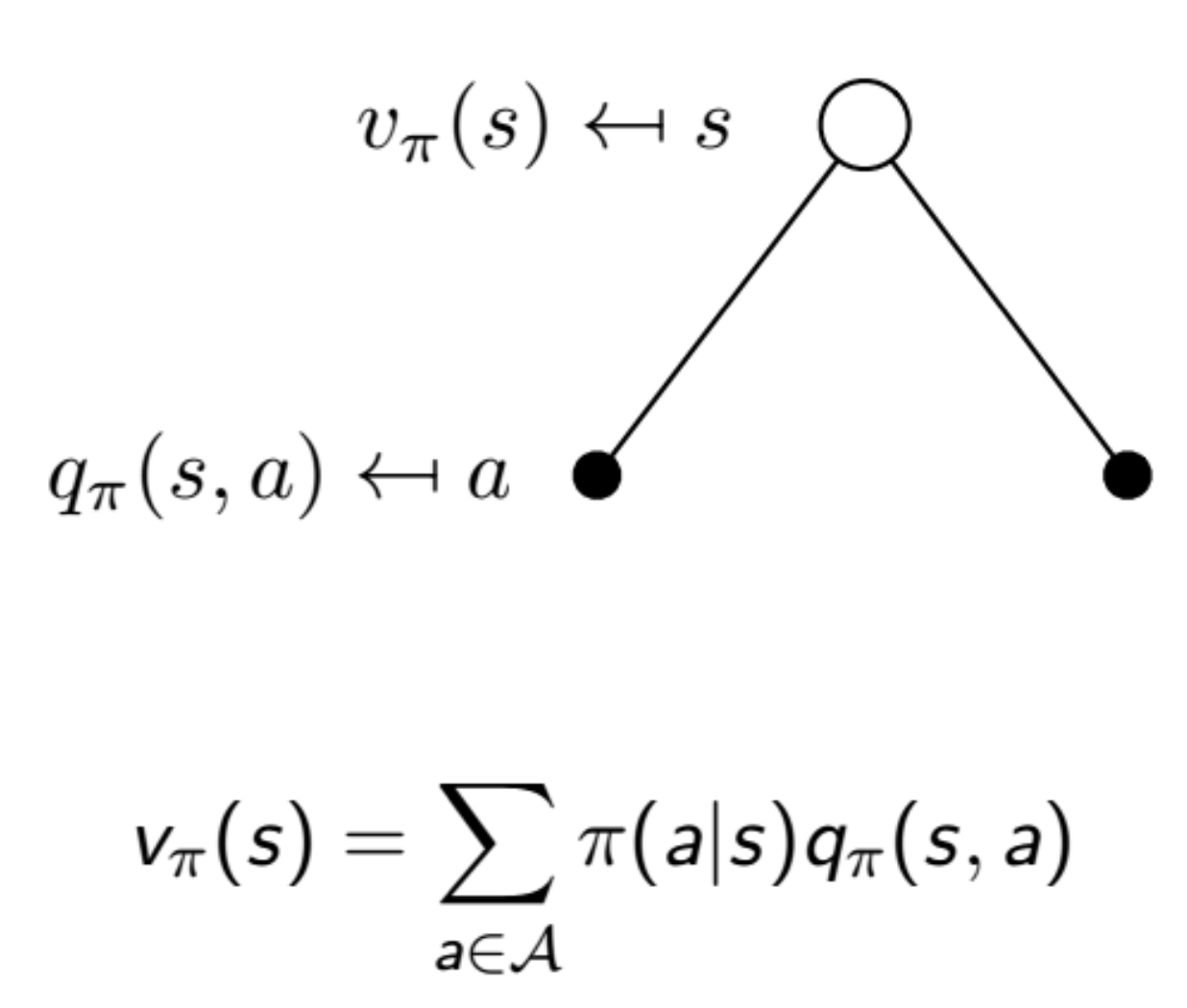
다음 수식은 $v_{\pi}$ Bellman Equation이다. 어떻게 보면 당연한 것을 알 수 있다. $v_{\pi}(s)$ 는 해당 수식의 의미는 해당 status에서 얻을 수 있는 reward의 expectation값이다.
action을 취할 확률인 policy $\pi(a|s)$와 해당 action을 취했을 때 얻을 수 있는 reward를 의미하는 $q_{\pi}(s,a)$를 모든 action에 대해서 더해주면 해당 state에서 얻을 수 있는 reward의 expectation값을 구할 수 있다.

$v_\pi$를 정리해보면 다음과 같다.
현재 state의 상태를 판단하기 위해, 각 action에 대한 value를 따진다.

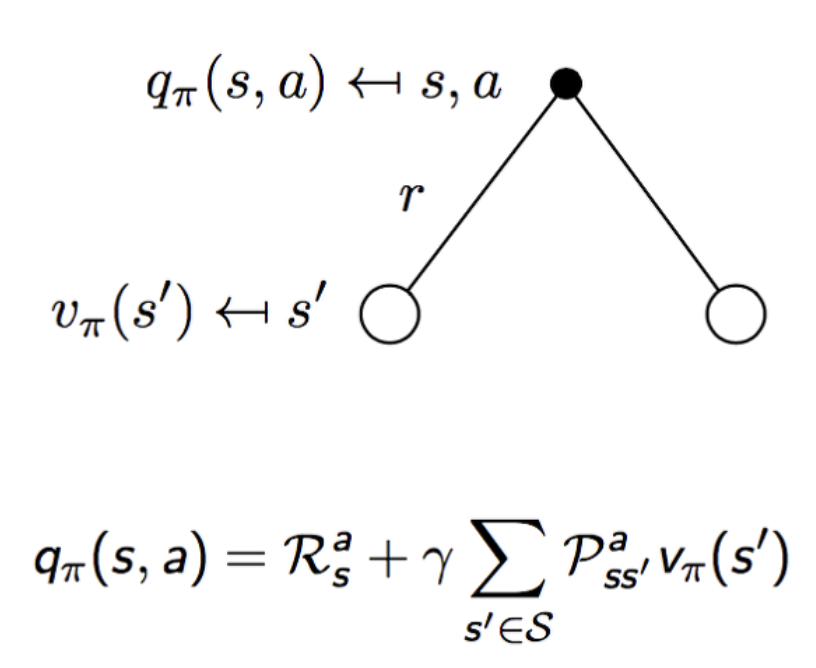
다음의 식은 action에 대해서 두가지 state가 나와서 맨처음에는 이해가 쉽게 되지 않을 수 있다.
다음의 상황은 주사위를 굴리는 action을 취했을때 짝수(state1)이 나올 수도 있고, 홀수(state2)가 나올수 있다.
1. $R_s^a$맨처음에 특정한 action을 취했을때의 reward값을 더해준다.
2. action에 대하여 각 state($s'$)로 이동할 확률 값 $P_{ss'}^a$과, 해당 state($s'$)에서의 value를 곱해준다.

$q_\pi$를 정리해보면 다음과 같다.
선택한 action에서 이동할 state에 대하여 value값을 계산하여 현재 action의 reward값을 계산한다.

results of value function

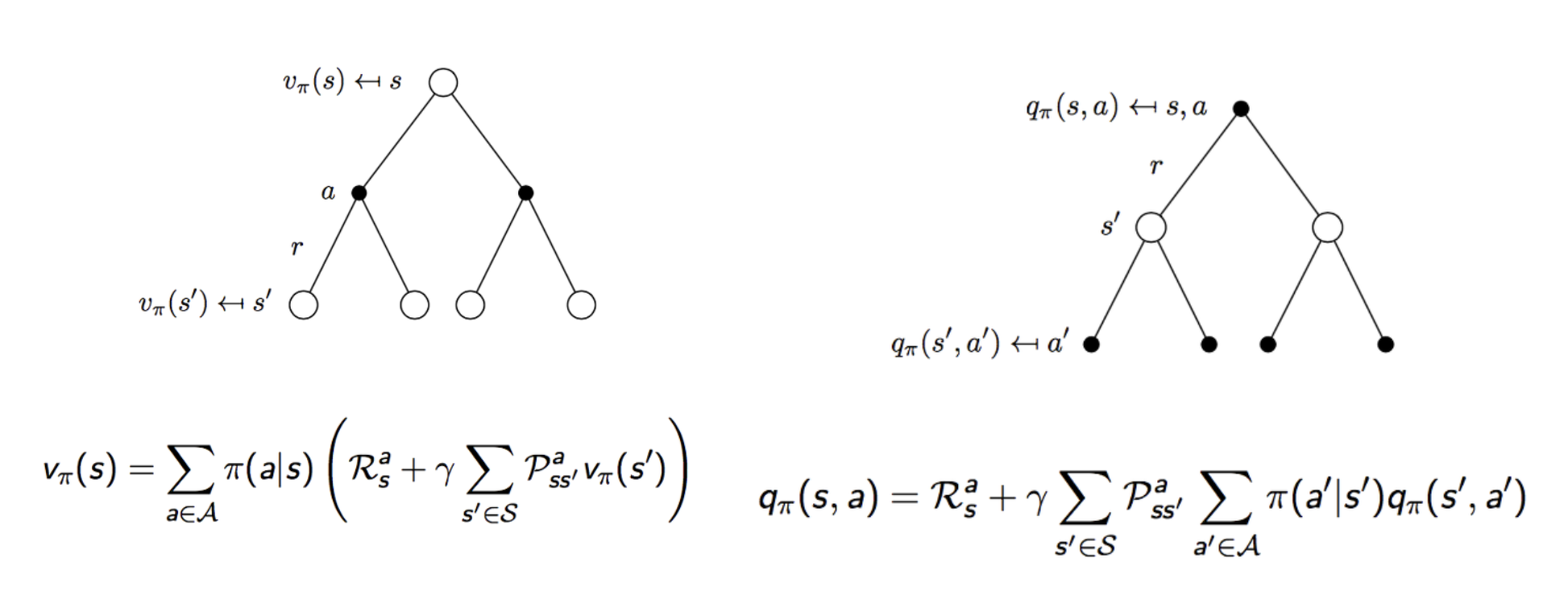
여태까지 배운 $v_\pi$와 $q_\pi$를 합쳐보면 다음과 같다.

$v_\pi$를 보면, 각각의 action에 대하여 해당 action에 대한 Reward의 값과 추후 이동할 state의 return값을 전부 계산한다.

$q_\pi$를 보면, 현재 선택한 action에 대해서 reward를 더한이후, 다음 state($s'$)에서 선택할 action에 대한 return값을 계산한다.

여기까지만 보면 아직 까지는 조금 추상적일 수 있지만, 예시를 보면 확실히 이해가 될 것이다.

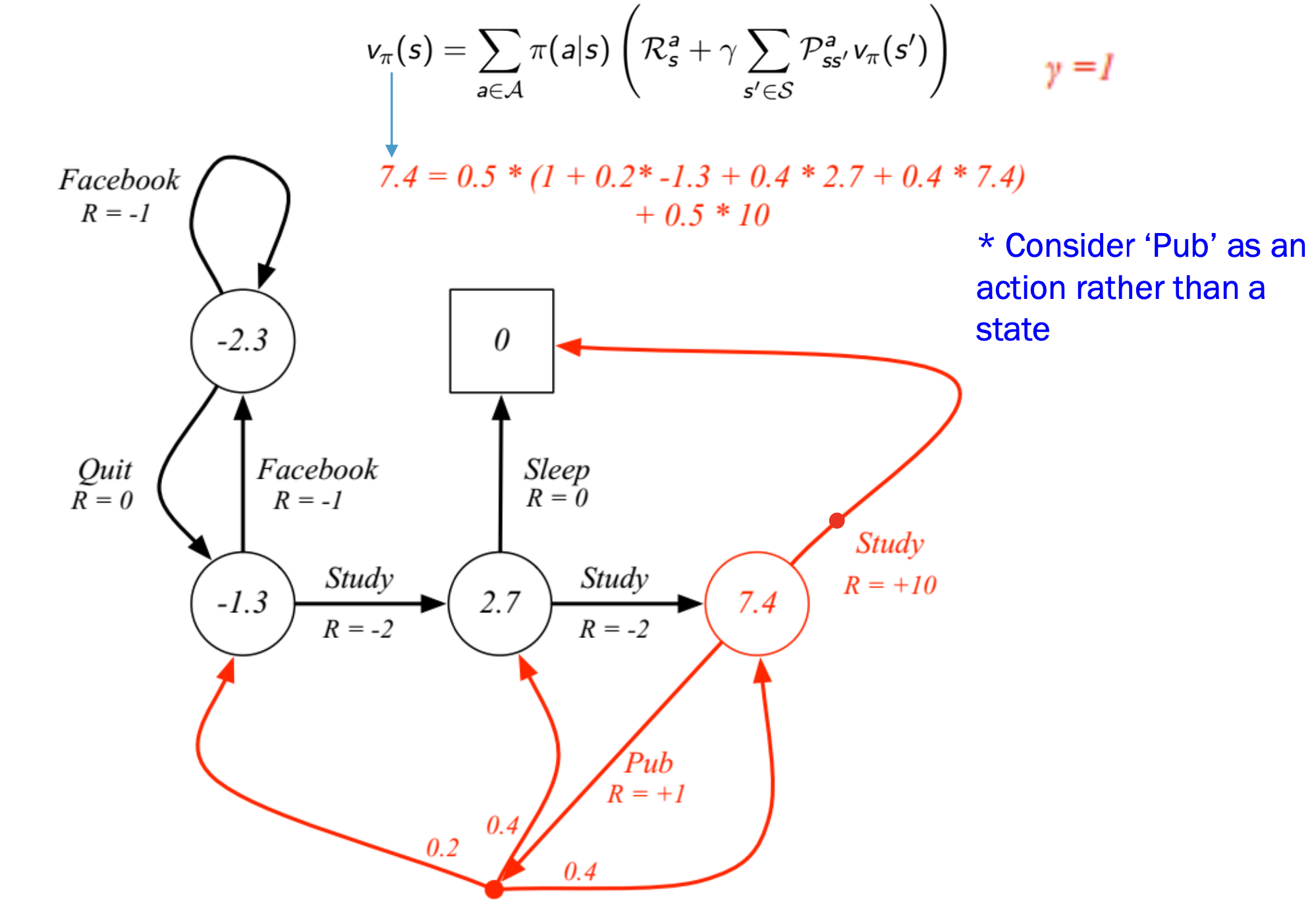
Class3에 대한 $v_\pi$를 구해보면 다음과 같다. 해당 이유는 취할 수 있는 policy는 Study와 Pub 두가지로 각각의 확률은 0.5 0.5이다.
Study를 선택하였을 경우 $0.5 \times10$인 이유는, 해당 action을 취했을때 reward로 10이 들어오고, 이동한 state의 경우 다른 state로 이동할 확률이 0이기 때문이다.
Pub을 선택하였을 경우 해당 action을 취할 policy가 0.5이고, Reward는 +1이다. 이후 Class1 Class2 Class3로 이동할 각각의 Policy와 해당 state의 value값을 곱하여 다 더해야 한다.

Optimal Solution

Markov Decision Process(MDP)에서는 최적의 value function을 찾는것이 목적이다.
최적의 value state function을 찾는 경우 state-value function이 최대값일때를 $v*$라 하고,
최적의 value action function을 찾는 경우 action-value function이 최대일때를 $q*$이라 한다.

Optimal Policy

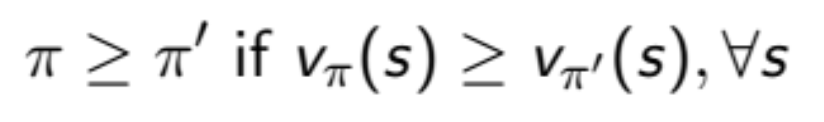
value값을 최대로 가지는 policy를 찾는 과정이다.
모든 상황에 대하여 최적의 값을 가지는 policy는 1개 또는 1개 이상 존재한다.
한가지 경우는 optimal state-value function의 값을 가지는 policy를 발견하는 것이고, 다른 한가지 경우 optimal action-value function을 가지는 policy를 발견하는 것이다.

Bellman Optimality Equation

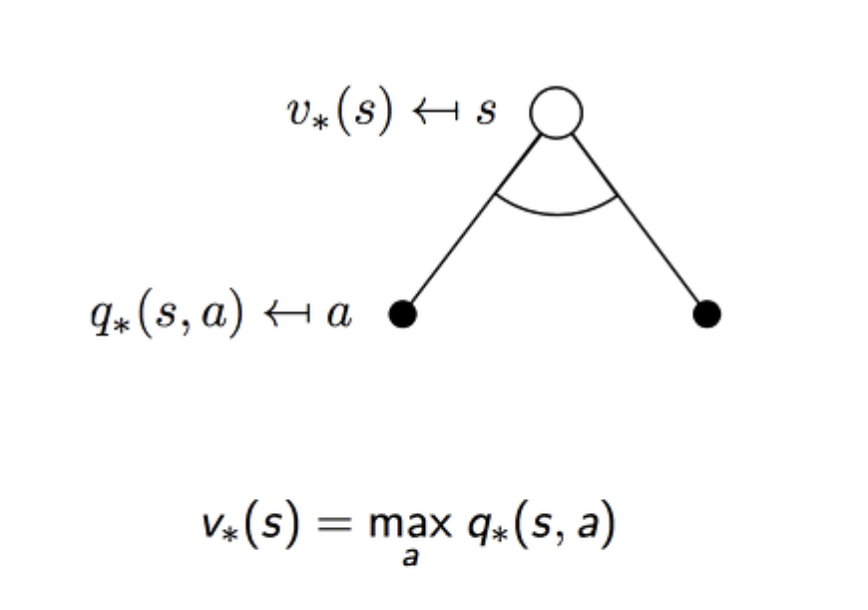
이제 해당 action에서 최댓값을 가지는 action을 선택한다. 즉 하나만 선택하는 과정을 다음과 같이 추가적인 기호를 더하여 표시한다. 즉 최대값을 가지는 $q*$을 선택한다.

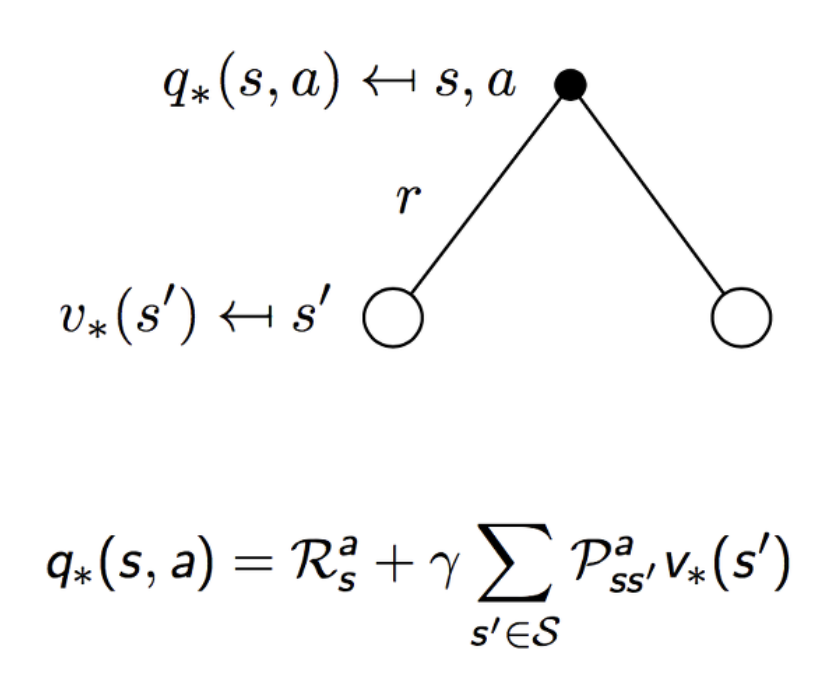
반면 optimal action-value function에서는 최댓값만을 취하는 것이 아닌, 특정한 action에 대한 state는 결정할 수 있는 부분이 아니기에, 확률적(stochastically)하게 결정된다.

optimal state-value fucntion to optimal state-value function의 그림을 보면 다음과 같다.

optimal action-value fucntion to optimal action-value function의 그림을 보면 다음과 같다.

두 optimal value function 모두 action을 취하는 곳에서만 maximum값을 취하는 것을 알 수 있다.

예시를 보면 다음과 같다.