RL(3) - Dynamic Programming

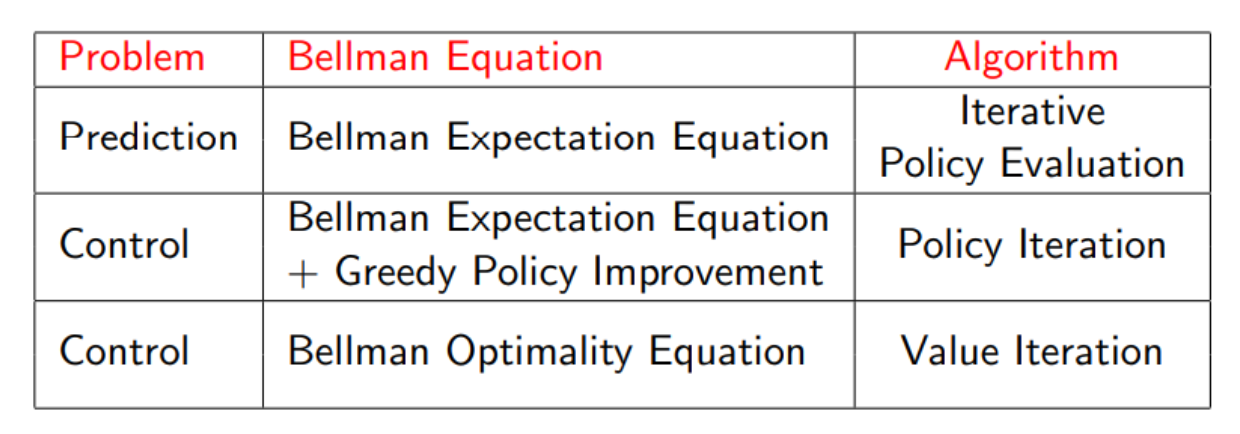
Dynamic Programming

과연 dynamic programming은 무엇일까?
어떻게 보면 programming이라는 이름이 들어가서 프로그래밍과 관련이 있다고 생각할 수 있으나, 여기서 programming의 의미는 저장한다는 의미이다.

Dynamic programming은 특정 problem을 풀기 해서 sub problem으로 나누어 sub problem을 해결한 내용을 바탕으로 합쳐 원래의 problem 을 푸는 방식이다.

조금 더 상세하게 설명을 하자면, Dynamic programming은 두가지 특징을 가지고 있다.
1. Optimal Substructure
문제의 최적 해결책이 그 문제의 부분 문제들의 최적 해결책으로 구성될 수 있다는 것을 의미한다.
예를들어 $F(n) = F(n-1) + F(n-2)$ 같은 문제가 이에 해당된다.
2. Overlapping sub-problems
중복되는 부분문제들의 반복적인 계산을 피함으로써, 훨씬 더 효율적인 연산이 가능하다.
기존에 해결하였던 정답의 경우 저장을 해놓는다.

Dynamic Programming의 이러한 개념들을 이용하여 효율성을 크게 향상시키고, 복잡한 문제들을 보다 쉽게 해결할 수 있다.

특히나 Dynamic programming을 이용하여 MDP에서도 동일하게 적용이 되고, Bellman Equation 과 Value function이 대표적인 특징을 가지고 있다.

Dynamic Programming을 이용한 planning

planning을 하기 위해서는 MDP의 모든 정보가 사전에 주어져야 한다.
왜냐하면 각각의 행동을 할 확률과, 각 state의 reward를 미리 알고 있어야 planning을 할 수 있다. 따라서 Markov Decision Process의 모든 요소들은 미리 알고 있다고 가정한다.

planning은 두가지가 존재한다.
1. Prediction
Input : $MDP(S, A, P, R, \gamma)$ and ploicy $\pi$ 또는 $MRP(S, P_\pi, R_\pi, \gamma)$
Output : value function $v_\pi$
2. Control
Input : $MDP(S, A, P, R, \gamma)$
Output : optimal value function $v*$ and optimal policy $\pi*$

Policy Evalution

우리는 이전에 배웠던 Bellman expectation을 반복적으로 사용하여 policy가 좋은지 나쁜지를 판단한다.
따라서 순차적으로 $v_1$부터 시작하여 $v_\pi$까지 구한다.
처음 시작되는 $v_1$의 경우 모든 state값이 0부터 시작될 것이다. 하지만 반복적으로 연산을 수행하면, 모든 state의 value값이 update가 될 것이고, 특정 값으로 수렴할 것이다. 이를 바탕으로 우리는 policy를 찾을 수 있다.

Synchronous backup

$v_{k+1}(s)$를 $v_k(s')$을 이용하여 업데이트를 진행한다.
이때 $s'$는 s의 이후 state들이다.

즉 이전 시나리오에서 이후 state들의 값을 이용하여 다음 시나리오의 이전 state의 value값을 구한다.

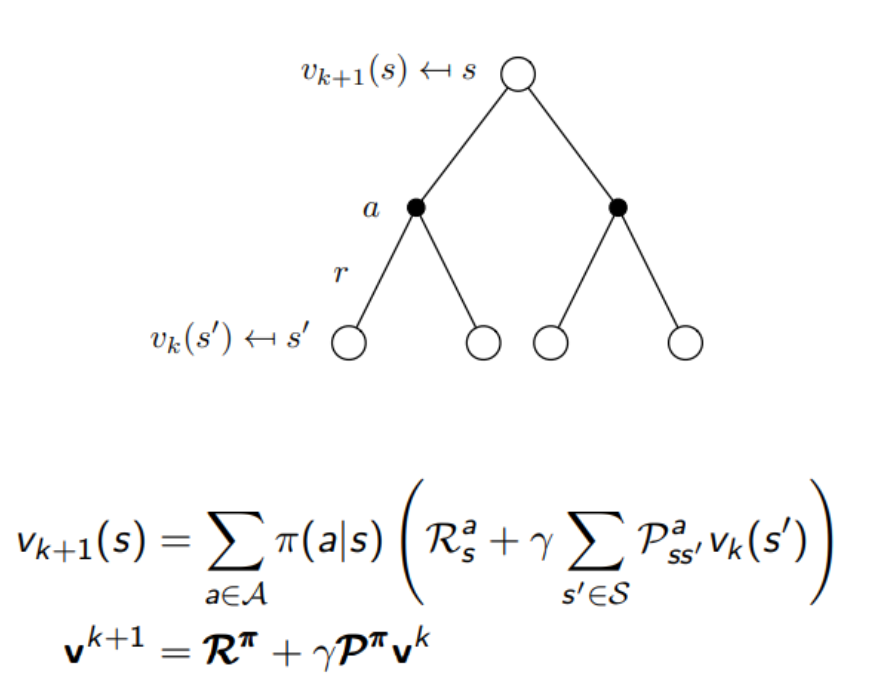
이를 수식과 그림을 이용하여 표현하면 다음과 같다. 해당 state는 다음 state들의 value 값을 이용하여 현재 state의 value를 구할 수 있으므로, 이전 scenario의 value값을 이용하여 구한다.

이를 바탕으로 예시를 보면 다음과 같다.

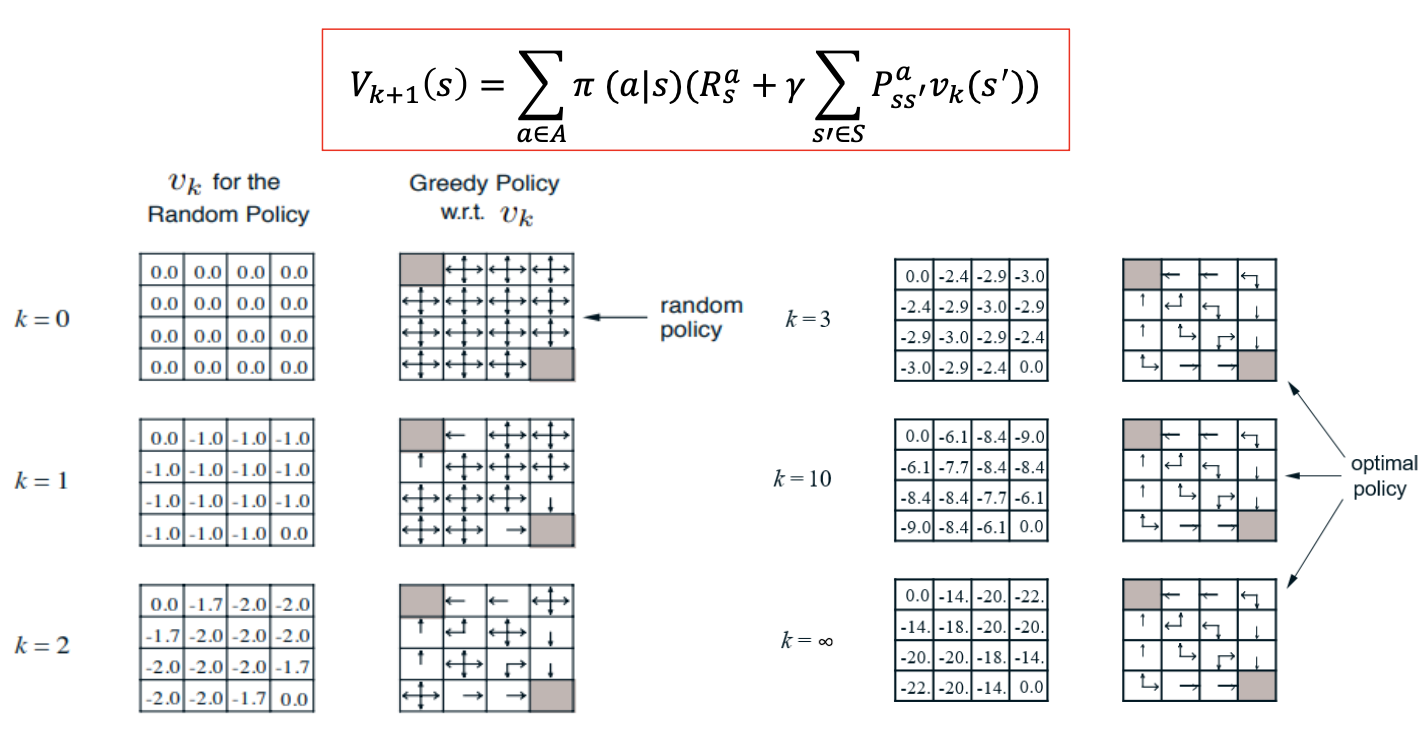
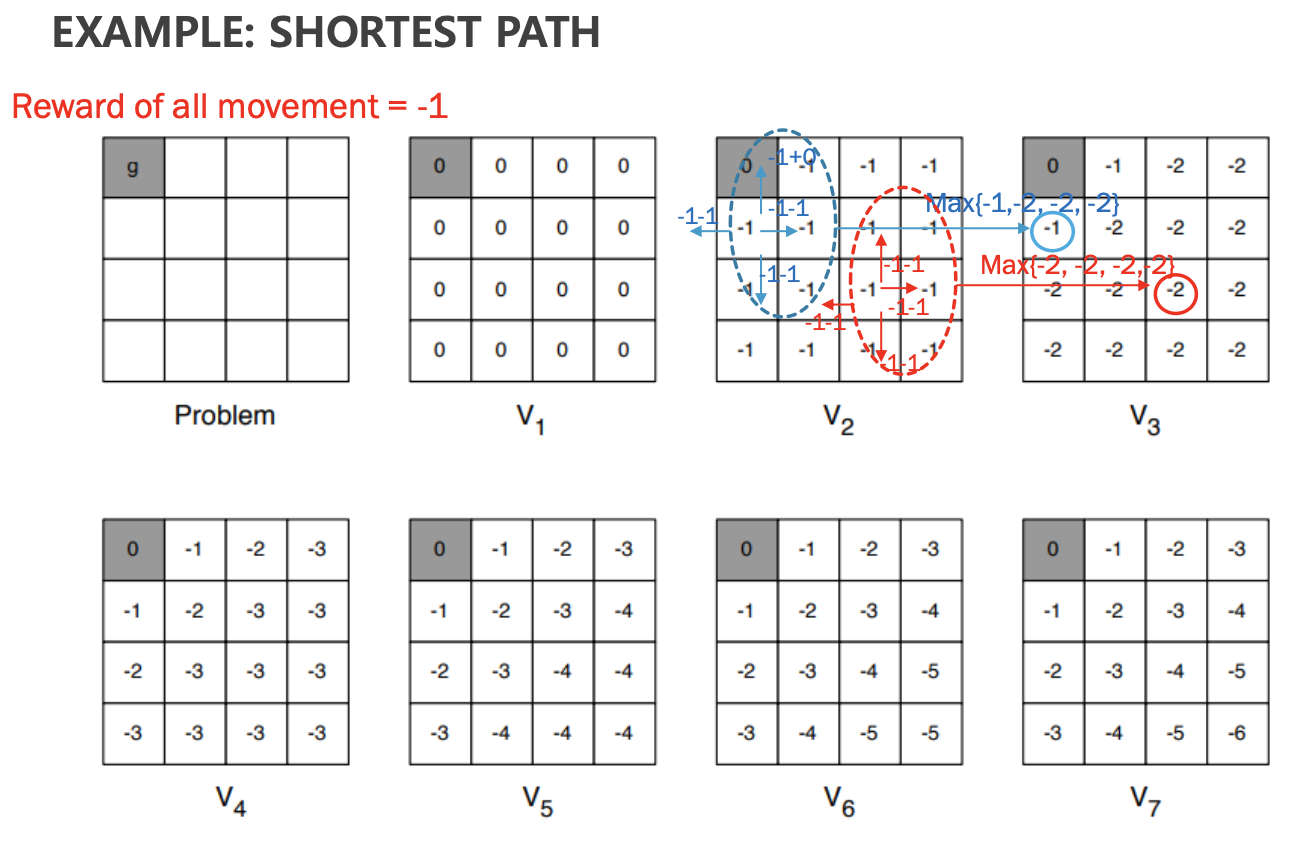
다음은 1부터 14까지의 state를 가지고 있는 grid world의 예제이다.
모든 action에 대한 reward는 -1으로 동일하다. 또한 policy는 동서남북 방향으로 동일한 0.25이다.
또한 나가게 되는 경우는 이전 state를 그대로 따르게 된다.

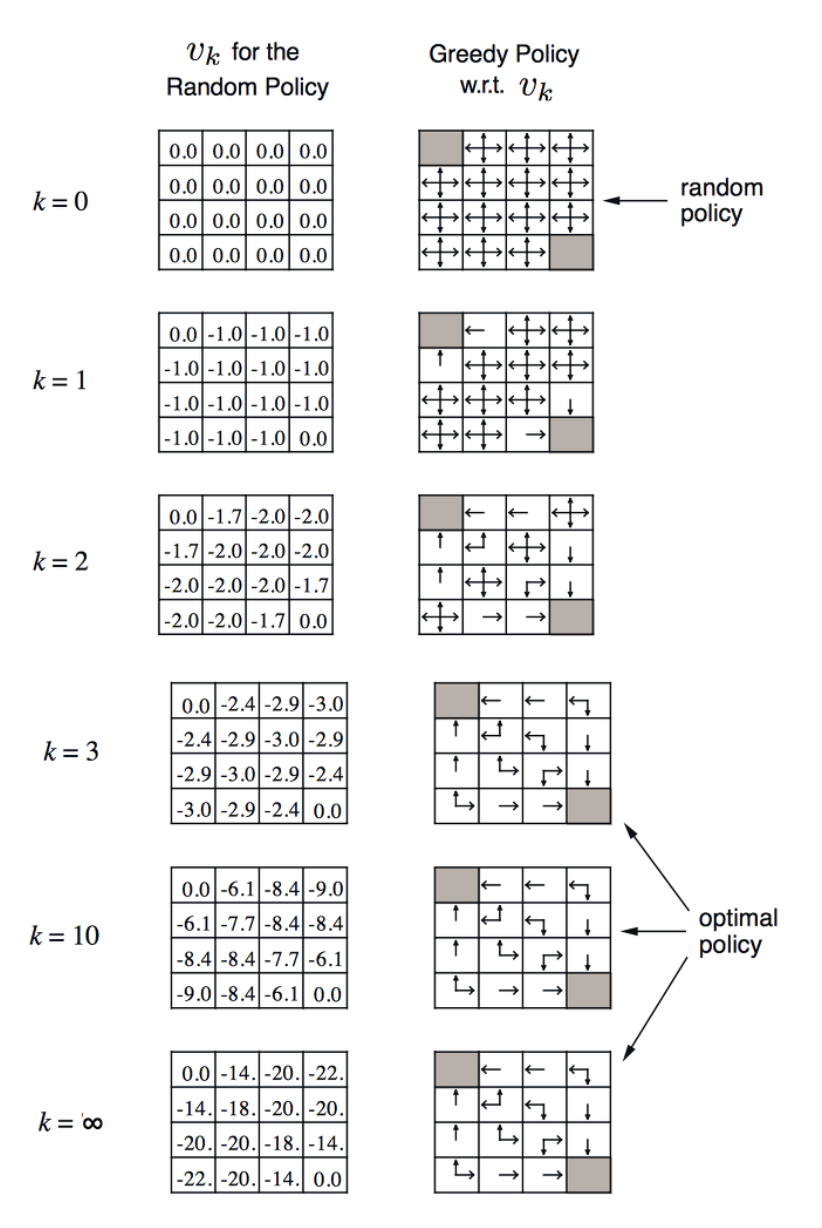
k가 0인 초기상태에서는 모든 state의 value값을 0으로 초기화를 진행한 상태에서 진행한다.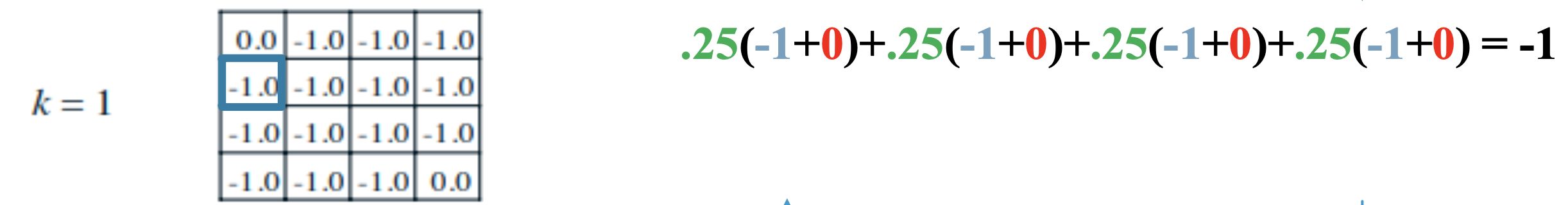
k가 1일때 [1,2]에서 -1.0을 어떻게 가지게 되는지를 판단하는 과정이다.
위쪽에서 $0.25\times(-1+0)$가 되는 것을 확인할 수 있고, 나머지 좌우아래에서도 동일한 값을 가지는 것을 확인할 수 있다.

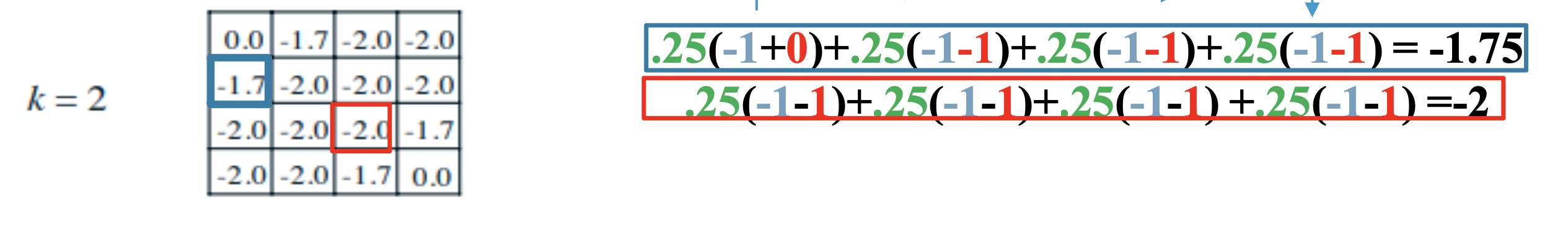
k가 2일때에도 식에서 제공된 내용과 동일하게 연산이 진행되는것을 확인할 수 있다.

이후 k값이 계속 증가하면서 각 state에 대한 value값이 특정한 값으로 수렴하는 것을 알 수 있다.
state값을 보면 agent는 더 높은 값을 향해서 가는게 이득이기에, 그 행동은 자연스럽게 policy를 따라 갈 것이다. 그리고 그러한 policy를 따라가다 보면 terminal state로 가게 됨을 알 수 있다.

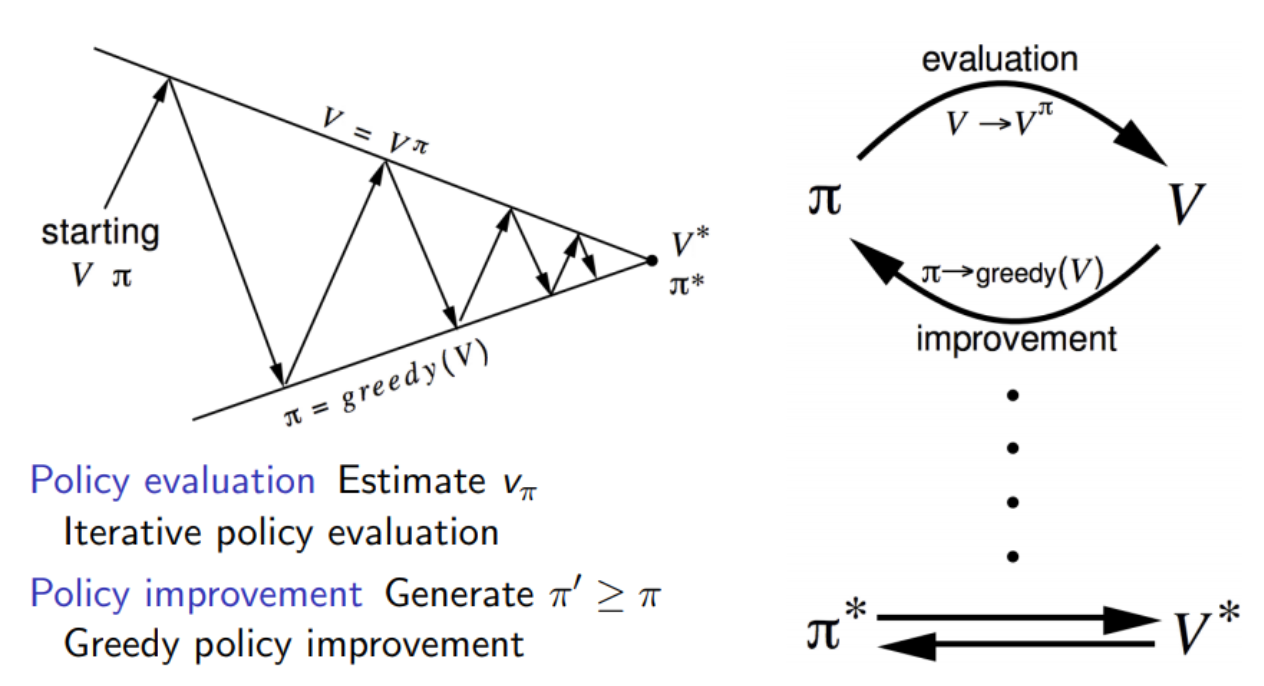
Policy Iteration

더 좋은 Policy를 만들기 위해서 Policy Iteration을 진행한다.
먼저 현재의 policy를 이용하여 value function을 구한다. 이러한 과정을 Evaluate라 한다. 그리고 이 value값과 action에 대한 value값을 비교하여 더 좋은 policy를 찾아가는 과정을 Improve라 한다.

즉 아까의 에제에서는 늘 각 policy의 값이 동서남북 방향으로 $0.25$로 동일하였는데, 이제 policy또한 update가 되며, 이를 바탕으로 Policy Evalution을 새롭게 진행하니 다른 값이 도출된다.

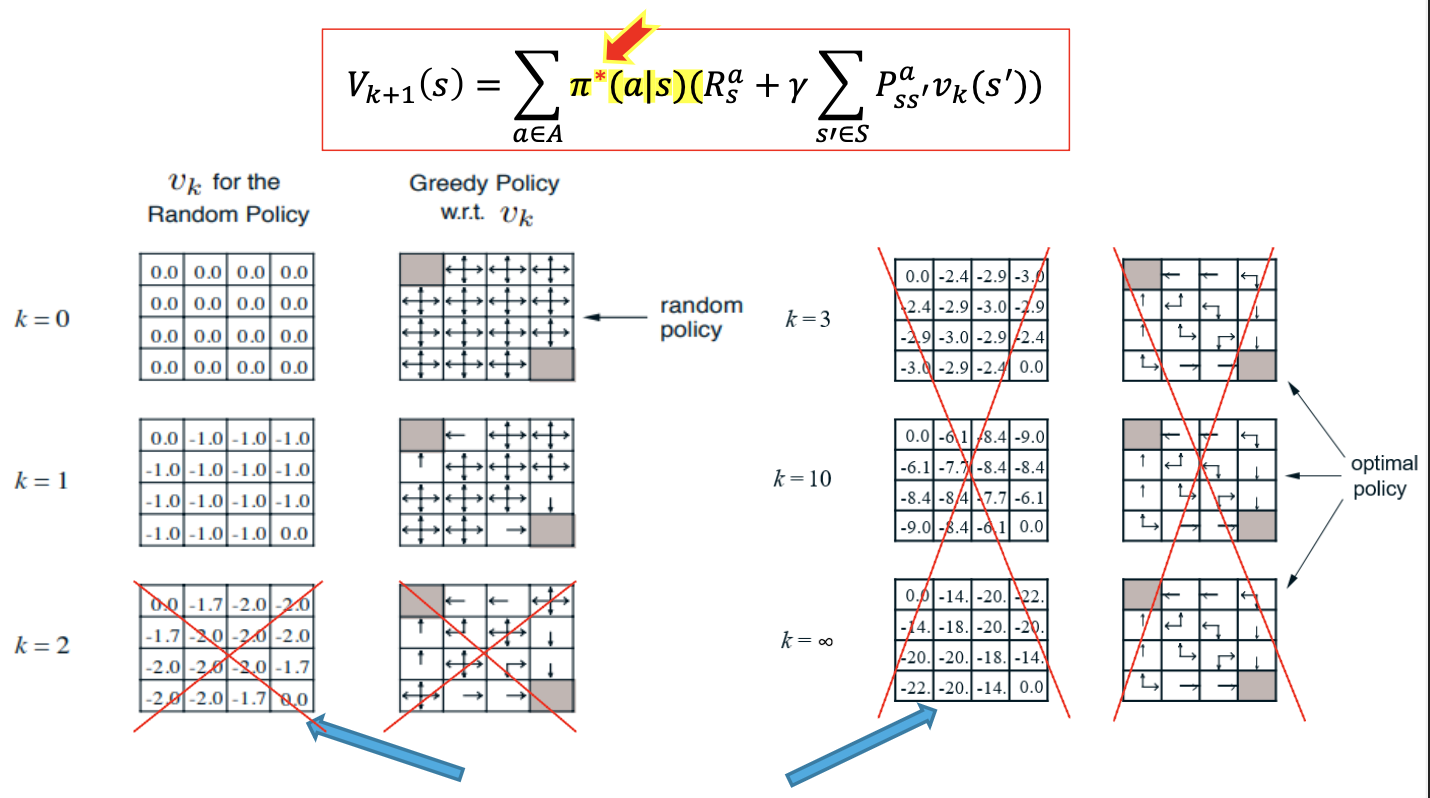
즉 위에서 구한 방식대로 policy를 $\pi(a|s)$를 사용하는 것이 아닌, greedy policy인 $\pi^*(a|s)$를 이용하여 구한다.

따라서 이를 이용하면서 $V^*$와 $\pi^*$에 수렴한다.

Value Iteration

만약 우리가 다음 state인 $s'$에 대해서 solution을 알고있다고 한다면, policy를 사용하지 않고서도, value값을 구할 수 있다. 그리고 해당 value값을 이용하여 optimal policy값을 구할 수 있다.

다음과 같이 max값을 이용하여 value값을 구할 수 있다. 이후 값을 이용하여 policy값을 도출할 수 있다.

이는 policy iteration과는 다르게 매 과정마다 policy를 도출할 필요가 없다. max만을 사용하기에 훨씬 빠르게 optimal policy에 접근할 수 있다.

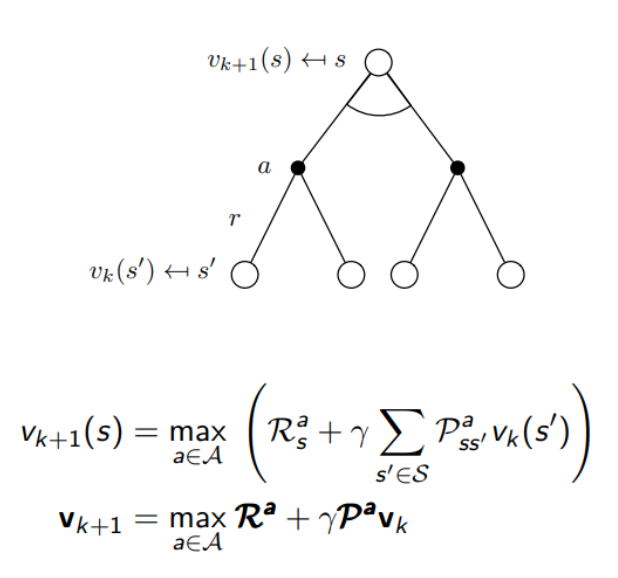
위의 value iteration의 수식과 그림이다.

이를 바탕으로 계산한 최종 Algorithm은 다음과 같다.