RL(4) - Monte Carlo Prediction

기존에 배운 Dynamic Programming에서는 MDP를 알고있다는 가정하에 문제를 풀었기에, Bellman Equation을 이용하여 최적화 정책을 찾았다.

그러나 모든 상황에서 MDP를 알 수 있는 상황이 있는 것은 아니다. 이러한 상황에서는 Model-free방식을 사용한다.

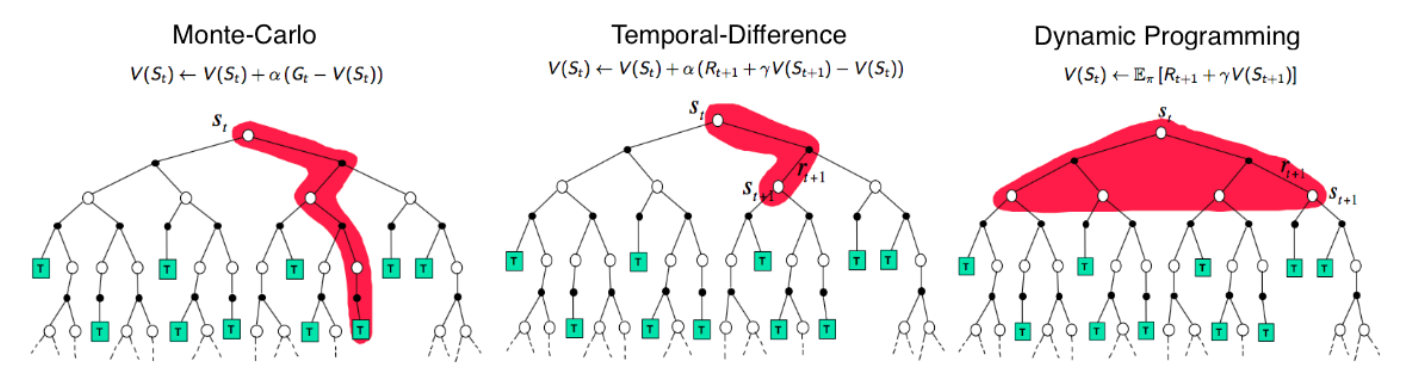
기존에 배웠던 Dynamic Programming에서는 다음과 같이 모든 action에 대한 가능성들의 Expectation을 계산하였다.

Monte Carlo Prediction

이번 Model-free에 해당하는 Monte Carlo Prediction 에서는 State가 어떻게 변하고, 어떠한 Reward가 모른지를 잘 모른다. 따라서 경험적인 정보들을 이용하여 해답을 찾아나간다.

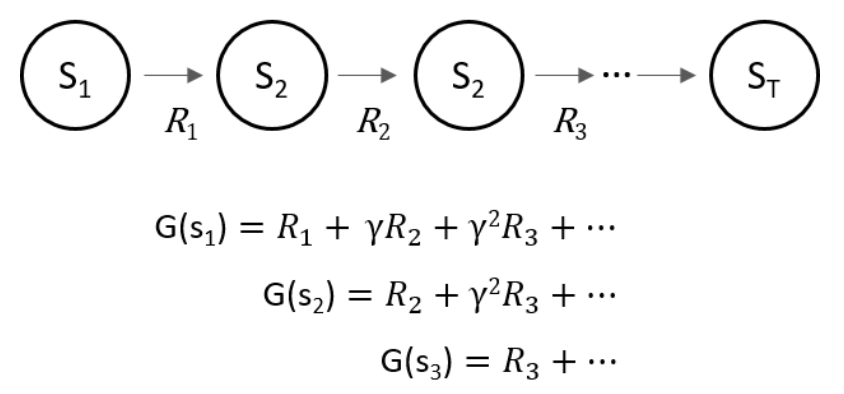
항상 에피소드가 완료되어 최종적으로 받는 보상의 평균을 구하여 학습을 진행한다.

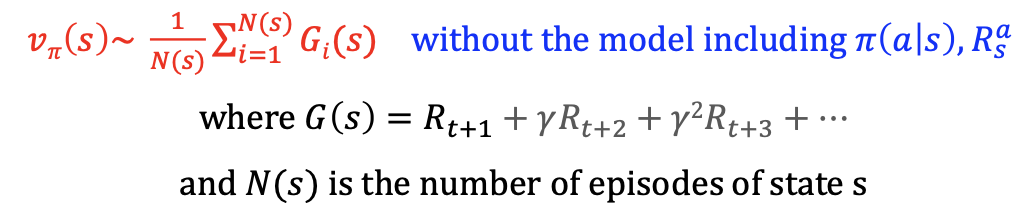
각 에피소드에서 얻은 Reward에 대한 평균값을 구하여 해당 state의 value를 구한다.

위의 식을 이용하여 $V_{n+1}(S_t) = \frac{1}{n}\sum_{n=1}^{n}G_i(S_t)$의 의미를 파해쳐 보자.
$\frac{1}{n}\sum_{n=1}^{n}G_i(S_t)$을 보면 여태까지 얻은 reward의 평균값을 이용하여 현재 state의 reward값을 판단할 수 있다.
하지만 이의 식을 정리한 결과인 $V_n(S_t) + \alpha(G_n(S_t)-V_n(S_t))$ 을 보면 여태까지 얻은 value에 대한 정보인 $V_n(S_t)$에 현재 얻은 차이정보를 더한 것을 확인할 수 있으며, 가중치인 $\alpha$의 값이 점점 작아지는 것을 통하여 update되는 정보의 값이 점점 작아지는 것이라 이해하면 된다.

Temporal Difference Prediction

다음과 같은 정보를 얻기 위해서는 해당 에피소드가 끝난 뒤에야 해당 state를 얻을 수 있다는 것이다.
만약 전투기의 자율주행을 목적으로 강화학습을 학습시킨다고 한다면, 매 에피소드가 끝나기 위해서는 매 전투기가 부셔져야 한다는 것이다. 이러한 문제를 방지하고자 하기 위해 Temporal Difference Prediction을 사용한다.

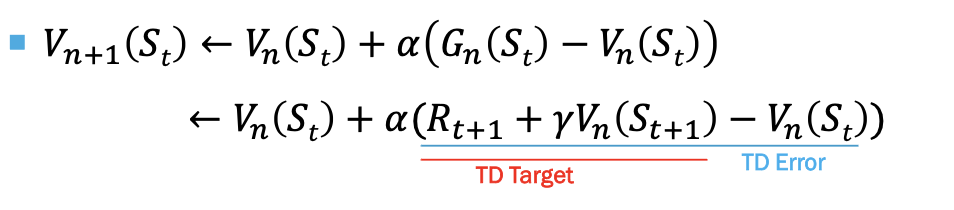
다음과 같이 $G_n(S_t)$을 $(R_{t+1}+\gamma V_n(S_{t+1})$로 변환하여 에피소드가 끝나기전에도 value를 update할 수 있도록 한다.

Reference

숨니의 무조건 따라하기 - https://sumniya.tistory.com/11