요약
-
AutoEncoder방식을 사용하여 유저나 아이템 벡터를 저차원의Latent feature로 표현(맵핑) -
decoder과정에서rating Matrix Completion을 수행 -
이때 학습은 관측된
rating에 대해서만 진행
AutoRec model
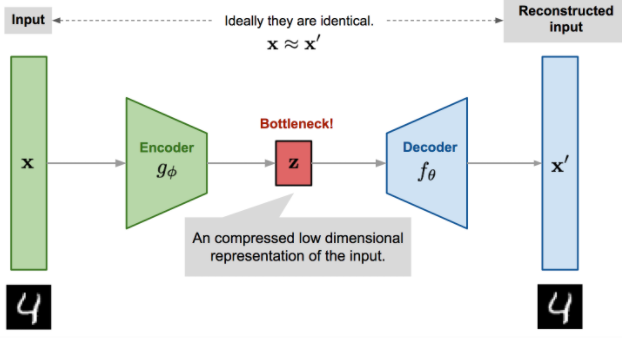
AutoEncoder
AutoRec을 설명하기 위해서 간단히 AutoEncoder가 무엇인지 알아보자.
AutoEncoder란?
-
encoder를 통해input data를Latent Variable(z)로embedding시키고(압축), -
decoder를 통해 다시input data로(최대한 원래 데이터와 비슷하게)재건(reconstructioin)하는 것
-
이때 SVD, PCA등과 같이 어떠한 수식적인 접근이 아닌
신경망을 통해encoding을 시키는데,encoder Network에서의weight를 학습하게 된다.
`AutoEncoder` 의 중요 포인트-
입력과 출력이 같은 구조
-
Bottleneck Hiddenlayer구조
Input Data
관측된 평점에 관한 벡터 or 가 input data
- --- item 에 관해서
관측된 평점
- --- user 에 관해서
관측된 평점
AutoRec 에서는 item based data인 를 위주로 설명한다.
Model
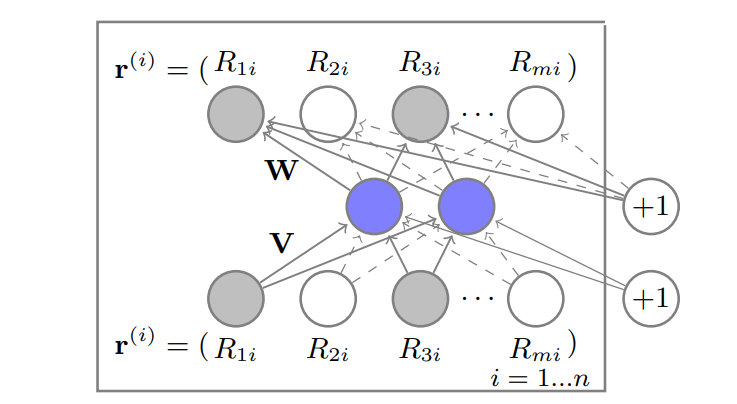
목적은 item-based autoencoder를 설계하는 것
는 input 으로 들어가서 latent(hidden) space로 매핑시키고
restructed 된 를 output으로 뽑아 missing rate를 예측한다.
이때 중요한 점은 관측된 데이터의 파라미터만 학습한다는 점인데 위 그림에서 회색 노드가 관측된 데이터를 뜻하고 실선이 업데이트를 진행한다는 뜻이다.
최종적인 예측값은
이 된다.
Loss
AutoRec 은 AutoEncoder 와 동일하게 RMSE를 최소화하는 Loss 식을 가진다.
--- ( 1 )
위 식은 (원래 rating 값) 과 의 차이의 L-2Norm을 최소화 한다.
이때 로 표현되는데
이는 모델의 예측 평점(restruction of input )을 뜻한다.
-
로 학습할 각 파라미터
-
: 활성화함수
--- (2)
식 (2) 는 기본적인 RMSE 를 최소화 시키는 식 (1) 에서 변화한 점이 두가지가 있다.
①
첫번째는 RMSE 식에서 에 윗첨자로 붙은 것을 볼 수 있는 데 이는 item-based AutoRec 이라는 뜻이다.
반대로 윗첨자에 가 붙어 가 된다면 user-based AutoRec을 한다는 뜻인데, 단순히 user 관점에서의 평점을 쓰는 것일 뿐 흐름에 큰 차이는 없다.
②
두번째는 규제항 ( ) 이 추가된 점이다.
이는 학습하는 파라미터()의 크기도 커지지 않게 조절한다.
최종적으로 식 (2)를 Loss Function 으로 활용하여 학습을 진행한다.
contribution
앞서 살펴본 Matrix Factorization(MF)와 다른점이 두개 존재한다.
-
MF는user와 item 모두latent space로 embed 하지만,
i-AutoRec은item만latent space로 embed 한다.(u-AutoRec은 user만 embed한다.) -
AutoRec은 활성화 함수 를 사용하여non-linear latent representation을 학습할 수 있다.
(MF는 linear latent representaion 밖에 학습할 수 없다. )
-> 표현력이 더 좋아진다.
궁금증
관측되지 않은 $$r$$ 은 어떻게 활용하는가?masked mse 를 통해 구현을 하자.
일단 input 에서 null 값을 0(논문에서는 3) 으로 채워서 AutoEncoder 모델에 넣는다.
reconstructed output(관측된 데이터, 관측안된 데이터 모두 복원됨) 에서의 원소 중 관측되었던 데이터 위치만 업데이트를 한다.
그렇게 되면 AutoEncoder는 참값들과 예측값(관측된 위치의)의 차이를 통해 기울기를 업데이트하게 된다.
Reference
https://lilianweng.github.io/lil-log/2018/08/12/from-autoencoder-to-beta-vae.html