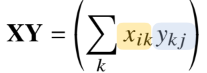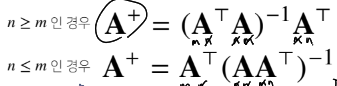이 글은 부스트캠프 AI Tech 3기 강의를 듣고 정리한 글입니다.

행렬 정의와 이해

벡터를 원소로 가지는 2차원 배열

행렬은 공간에서의 "여러점" 을 나타냄

• 행벡터 X_i는 i번쨰 데이터를 의미

행렬은 벡터공간에서 사용되는 연산자 로 이해

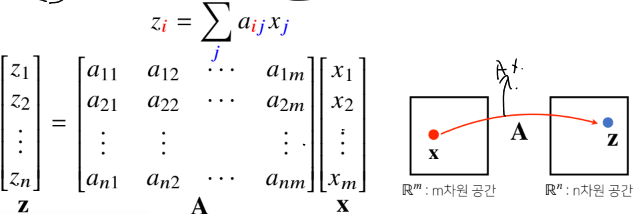
• 행렬곱을 통해 벡터를 다른차원의 공간으로 보낼 수 있음
• 행렬곱을 통해 패턴을 추출 할 수 있고, 데이터를 압축 할 수 있음
• 모든 선형 변환은 행렬 곱으로 계산 가능
  ※ DL에서는 선형변환과 비선형 함수(softmax,Relu, ...)의 합성으로 이루어져 있음

행렬 연산

행렬의 덧셈 뺼셈 성분곱 스칼라곱

같은 모양을 가지면 +, -, ⊙, 스칼라곱 가능

• 방식은 벡터의 덧셈, 뺄셈, 성분곱과 같음
  • 같은 위치의 원소 끼리 +,-,x

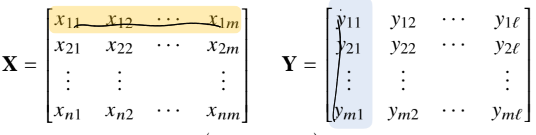
행렬곱(Matrix Multiplication)

앞행렬의 열의 개수 == 뒷행렬의 행의 개수

• XY 계산시
  • X의 열의 개수 == Y의 행의 개수
  • (n m)(m a) => n*a
    

결과의_ij = i번쨰 행백터와 j번쨰 열백터의 내적

• 'numpy' 에서는 '@' 사용

import numpy as np
X = np.array([1,2,3],[4,5,6],[7,8,9]]
y = np.array([1,2,3],[4,5,6],[7,8,9]]
X @ Y # X와 Y의 행렬곱

행렬의 내적?

• 수학에서 말하는 내적과는 다름

• XY^T로 계산됨
  

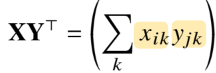
• np.inner 사용 : i번째 행백터와 j번째 행벡터 사이의 내적을 가지는 성분으로 행렬 생성

import numpy as np
X = np.array([1,2,3],[4,5,6],[7,8,9]]
y = np.array([1,2,3],[4,5,6],[7,8,9]]
np.inner(X,Y) # X와 Y의 내적

역행렬

어떤행렬의 연산을 거꾸로 되돌리는 행렬을 역행렬(inversematrix)

역행렬은 행과 열 숫자가 같고 행렬식(determinant)이 0이 아닌 경우에만 계산

import numpy as np
X = np.array([1,2,3],[4,5,6],[7,8,9]]
np.linalg.inv(X) # 역행렬 구하는 함수 

역행렬을 계산할수 없다면 유사역행렬 or 무어펜로즈 역행렬을 이용

import numpy as np
X = np.array([1,2,3],[4,5,6],[7,8,9]]
np.linalg.pinv(X) # 무어펜로즈 역행렬 구하는 함수 

무어펜로즈 역행렬을 이용하면

• 연립방정식의 해 중 하나를 구할 수 있다.
  
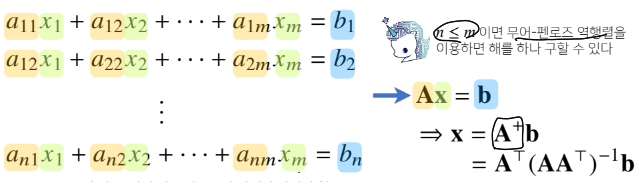
  부정 또는 무수히 많은 해라고 불리는 연립방정식에서 수많은 해중 하나의 해를 구할 수 있다.

• 선형회귀식을 찾을 수 있다.
  np.linalg.pinv(X)를 사용
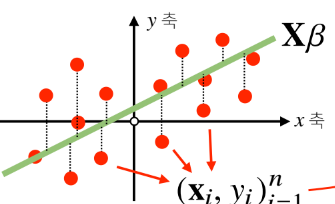
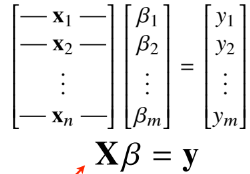  에서 계수 B를 찾아야 한다.
  모든 데이터((x,y)쌍)가 선형으로 되어있지 않기 때문에 방정식을 푸는 것은 불가능
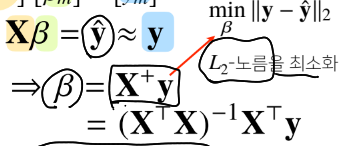  무어펜로즈 역행렬을 이용하면 y에 근접하는 y^을 찾을 수 있다.
  

행렬의 응용