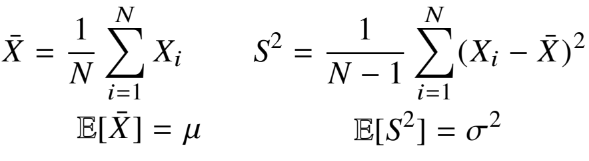이 글은 부스트캠프 AI Tech 3기 강의를 듣고 정리한 글입니다.
모수란?
- 통계적 모델링은 적절한 가정 위에서 확률 분포를 추청하는 것이 목표이다.
- 이는 기계학습과 통계학이 공통적으로 추구하는 목표
- 기계학습에서 통계학을 애용하는 이유는 통계학의 간편함이 기계학습의 하드웨어적 부담을 덜어주기 때문이라고 한다.
- 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아낸다는 것은 불가능
- 따라서 근사적으로 확률분포를 추정할 수 밖에 없다.
- 예측모형의 목적 : 분포를 정확하게 맞추기 보다 데이터와 추정방법의 불확실성을 고려하여 위험을 최소화 하는 것
- 모수적(parametric) 방법론 : 데이터가 특정 확률 분포를 따른다고 가정한 후 그 분포를 결정하는 모수를 추정
- 비모수적(nonparametric)방법론 : 확률분포 가정x / 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀜
- 기계학습의 많은 방법론은 비모수 방법론에 속한다
- "모수가 없다" 가 아니라 "모수가 무한대"or "모수의 개수가 데이터에 따라서 바뀌는 경우"로 이해 하는 것이 좋다.
확률 분포 가정
확률분포를 가정하는 방법
-
우선 히스토그램을 통해 모양을 관찰
- 데이터가 2개의 값만 가지는 경우 -> 베르누이 분포
- 데이터가 n개의 이산적인 값을 가지는 경우 -> 카테고리 분포
- 데이터가 [0, 1] 사이의 값을 가지는 경우 -> 베타분포
- 데이터가 0 이상의 값을 가지는 경우 -> 감마분포, 로그정규분포 등
- 데이터가 실수 정체에서 값을 가지는 경우 -> 정규분포, 라플라스분포 등
-
해당사항이 있다고 기계적으로 확률분포를 가정해서는 안되며, 데이터를 생성하는 원리를 먼저 고려하는것이 원칙
- 각 분포마다 검정하는 방법이 있으니 모수 추정한 뒤 반드시 검정해보도록 하자
데이터로 모수 추정
데이터의 확률분포를 가정했다면 모수를 추정해 볼 수 있다.
정규분포의 모수 추정
이항 분포에서
- 정규분포의 모수는 평균과 분산으로 이를 추정하는 통계량은 다음과 같다.
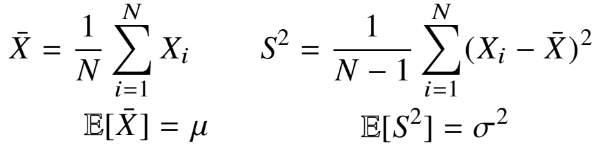
-
통계량(not 표본) 의 확률분포를 표집분포(sampling distribution)라 부르며, 특히 표본평균의 표집분포는 N이 커질수록 정규분포를 따른다
-
이를 중심극한정리라 부르면 모집단의 분포가 정규분포를 따르지 않아도 성립!
-
이항분포에서 통계량(평균) 을 계속 뽑아 그래프를 그려보면 다음과 같다.
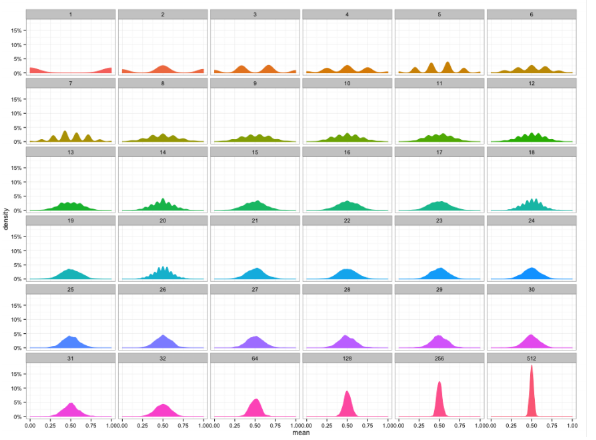
- 이처럼 계속해서 통계량을 뽑을 수록 정규분포에 가까워지고 있다.
-
최대 가능도 추정법(Maximum Likelihood Estimation)
MLE의 필요성
- 표본평균이나 표본분산은 중요한 통계량이지만
- 확률분포마다 사용하는 모수가 다르기 때문에 적절한 통계량이 달라진다
- 이때 가장 적절한 모수를 찾을 수 있는 것이 MLE 이다.
MLE의 의미
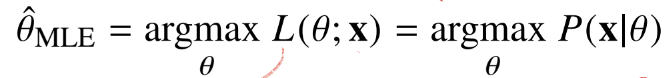
모수(θ)를 따르는 분포가 데이터 X를 관찰할 가능성을 뜻한다.
여기서 주의할 점은 θ에 대한 MLE 값을 확률로 해석하면 안된다. (θ에 대해서 적분하게 되면 1이 나오지 않기 때문에)
그냥 각 θ에 대해서 대소비교가 가능한 것 정도로 이해하면 된다.
로그가능도
- 데이터 집합 X가 독립적으로 추출되었을 경우 로그 가능도를 최적화한다.
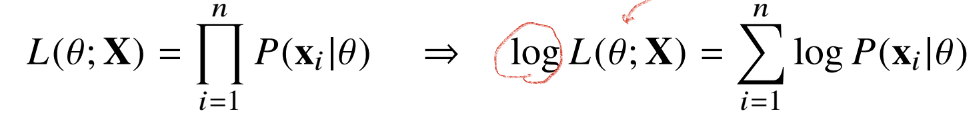
왜 로그가능도인가?
로그 가능도, 가능도 모두 MLE가 될수 있다.
하지만 보통 로그 가능도를 사용하게 되는데, 이는 최적화 관점에서 좋기 때문이다.
- 만약 [0, 1] 범위의 데이터 개수가 수억단위가 된다면 컴퓨터의 정확도로는 가능도를 계산하는 것이 불가능
- 데이터가 독립이라면, 로그는 곱셈을 덧셈으로 바꿀수 있기 때문에 컴퓨터로 연산이 가능
- 경사하강법으로 가능도 최적화시 미분연산을 사용하는데 연산량을 O(n2)->O(n)으로 낮춰줌
- 손실함수의 경우, 경사하강법을 사용하므로 음의 로그가능도를 최적화
MLE 예제1 : 정규분포
정규분포를 따르는 확률변수 X로 부터 독립표본 {x_1, ... , x_n}을 얻었을 때 MLE추정법을 이용하여 모수를 추정하면?

θ에 정규분포식을 대입하여 계산한 결과 마지막수식의 결과가 나오게 된다.
이때 마지막 수식을 평균과 분산에 대해서 각각 미분을 해주면 최적화할 수 있다.

-
이때 MLE는 불편추정량과 식이 거의 같지만 불편추정량을 보장하진 않는다
-
단 Consistentcy(일치성 : n이 커짐에 따라 모수에 근접하는 성질)은 보장한다.
MLE예제2 : 카테고리 분포
카테고리 분포 (Multinoulli)를 따르는 확률변수 X 로부터 독립표본 {x_1, ... , x_n}을 얻었을 때 MLE추정법을 이용하여 모수를 추정하면?

이때 오른쪽 제약식을 만족하면서 목적식을 최대화 하는 것이 우리가 구하는 MLE이다.
목적식에 제약식이 있기 떄문에 바로 미분을 하지 않고 라그랑주 승수법을 통해 새로운 목적식을 만들어 MLE를 구하게 된다.
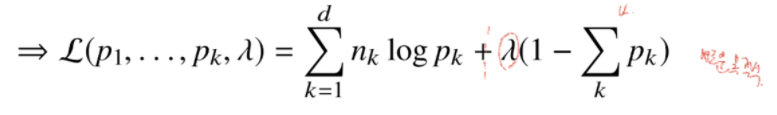
각각의 모수에 대하여 미분하고 라그랑주 승수에 대하여 미분하여 값을 구하게 된다.

결국 카테고리 분포의 MLE는 경우의 수를 세어서 비율을 구하는 것이라는 직관적인 모수가 나오게 된다.
딥러닝에서의 MLE
- MLE를 통해 기계학습 모델을 학습할 수 있다.
- 딥러닝 모델의 가중치를 θ=(W^1, ... ,W^L)이라 표기 했을 때 분류 문제에서 소프트맥스 벡터는 카테고리 분포의 모수(p_1, ..., , p_k)를 모델링 한다
- 원핫벡터로 표현한 정답레이블 y=(y_1, ... , y_k)을 관찰데이터로 이용해 확률분포인 소프트맥스 벡터의 로그가능도를 최적화 할 수 있다.
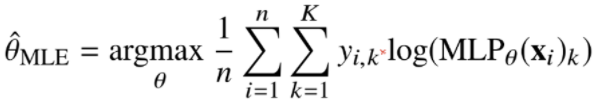
확률 분포의 거리
-
기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도
-
데이터 공간에 두개의 확률분포 P(X), Q(X)가 있을 경우 두 확률분퐈이의 거리는 다음의 함수들을 이용
- 총변동거리 (Total Variation Distance, TV)
- 쿨백-라이블러 발산(Kulback-Leibler Divergence, KL)
- 바슈타인 거리(Wasserstein Distance)
쿨백 - 라이블러 발산
교차 엔트로피와 함께 보면 좋은 개념이라 따로 정리 하였다.
쿨백 - 라이블러 발산 정리(with Entropy & Cross Entropy)
정의

분해

- 분류문제에서 정답레이블 P, 모델 예측을 Q라 두면 최대가능도 추정법은 쿨백-라이블러 발산을 최소화 하는 것과 같다.