AI_math

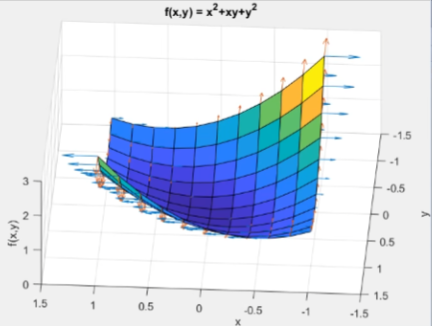
미분의 간단한 정의와 경사하강법에서 왜 미분이 필요한지 아라보자! SGD의 기초적 개념도 아라보쟈

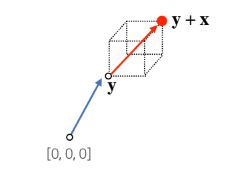
x = x_1, x_2, ... n차원 공간(원소의 개수n) 에서의 한 점1차원 : 스칼라2차원 : 평명3차원 : 입체원점으로 부터 상대적 위치 => 숫자(스칼라)를 곱해주면 길이만 변함 (벡터의 스칼라곱)a > 1 : 길이가 들어나고a < 1 : 길이가 줄어들

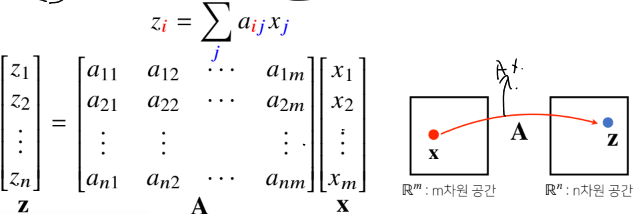
imageimage 행벡터 X_i는 i번쨰 데이터를 의미행렬곱을 통해 벡터를 다른차원의 공간으로 보낼 수 있음행렬곱을 통해 패턴을 추출 할 수 있고, 데이터를 압축 할 수 있음모든 선형 변환은 행렬 곱으로 계산 가능※ DL에서는 선형변환과 비선형 함수(softmax,

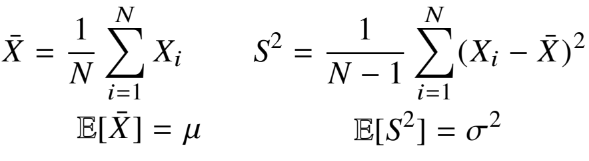
통계적 모델링은 적절한 가정 위에서 확률 분포를 추청하는 것이 목표이다.이는 기계학습과 통계학이 공통적으로 추구하는 목표기계학습에서 통계학을 애용하는 이유는 통계학의 간편함이 기계학습의 하드웨어적 부담을 덜어주기 때문이라고 한다.유한한 개수의 데이터만 관찰해서 모집단의

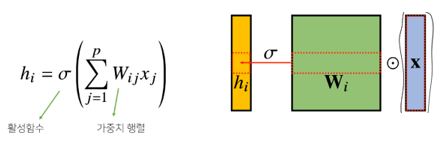
기본적인 다층신경망(MLP)는 각 뉴런들이 선형모델과 활성함수로 fully-connected된 구조각 $$h_i$$ 에 대응하는 가중치 행 $$W_i$$ 가 필요한데 \* 이때 i가 바뀌면서 사용되는 가중치도 바뀌게 된다. Convolution연산은 커널(kerna

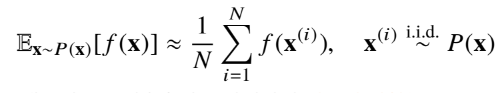
기계학습에서 사용되는 손실함수(Loss Function)들의 작동원리는 데이터 공간을 통계적으로 해석해서 유도함 컴퓨터로 수식을 해석적으로 계산하는 것은 힘들기 때문에 딥러닝 또한 확률론 기반의 기계학습이론에 바탕을 두고 있다이에 대한 예시로 몬테카를로 샘플링을 들

개요 딥러닝은 신경망[선형모델 / 활성함수]의 여러층에 대한 합성함수이기 때문에 gradient 계산을 위해 연쇄법칙을 적용한 역전파를 사용한다. 신경망을 분해 신경망은 기본적으로 선형모델이 아닌 비선형 모델이다. 신경망을 수식적으로 분해해 보면 선형모델과

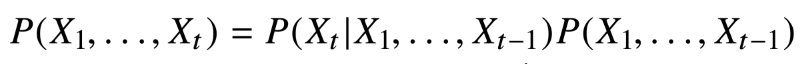
RNN은 구조자체는 어렵지 않지만 왜 그렇게 해야하는지 수식을 통해 이해가 필요하다시퀸스 데이터란소리, 문자열, 주가 등 시간에 따라 변화하는 데이터를 시퀸스(sequence) 데이터라고 한다시퀸스 데이터는 i.i.d(독립동등분포)가정을 잘 위배하기 때문에 순서를 바꾸

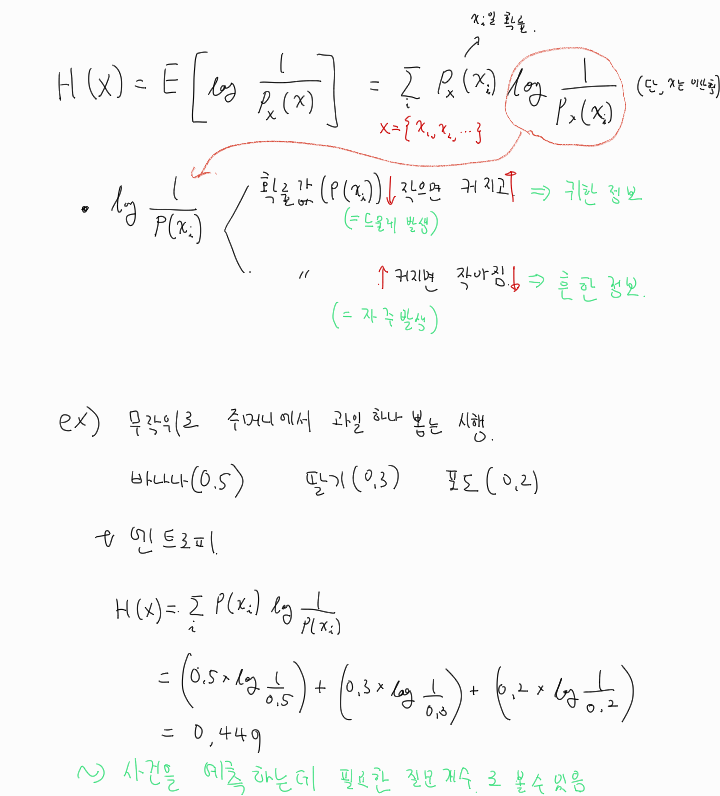
사전적 정의 : 열역학적계의 유용하지 않은(일로 변환할 수 없는 ) 에너지의 흐름을 설명할 때 이용 되는 상태함수통계적 의미 : 어떤 사건이 정보적 측면에서 얼마나중요한가를 반영한 로그 지표에 대한 기댓값을 구한 것실제 분포와 예측 분포가 다르다는 특징을 이용해, 실제