이 글은 부스트캠프 AI Tech 3기 강의를 듣고 정리한 글입니다.
K-Nearest Neighbors CF
NBCF의 한계
NBCF 는 아이템 i에 대한 평점을 예측하기 위해서는 Ω i \Omega_{i} Ω i
Ω i \Omega_{i} Ω i i i i
이때 유저가 많아질수록 계속해서 연산량을 늘어나게 되고 오히려 성능은 떨어지기도 한다.
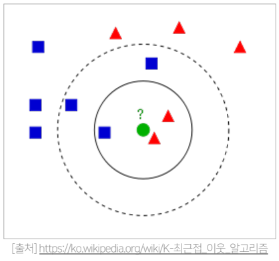
KNN 협업 필터링 기본 아이디어
Ω i \Omega_{i} Ω i u u u
K는 보통 25~30 을 많이 사용하지만 사용자가 설정해주어야 한다 (하이퍼파라미터)
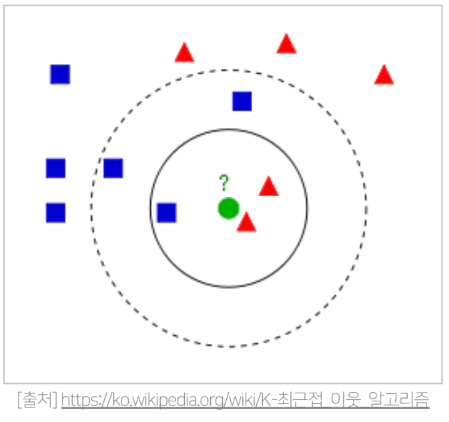
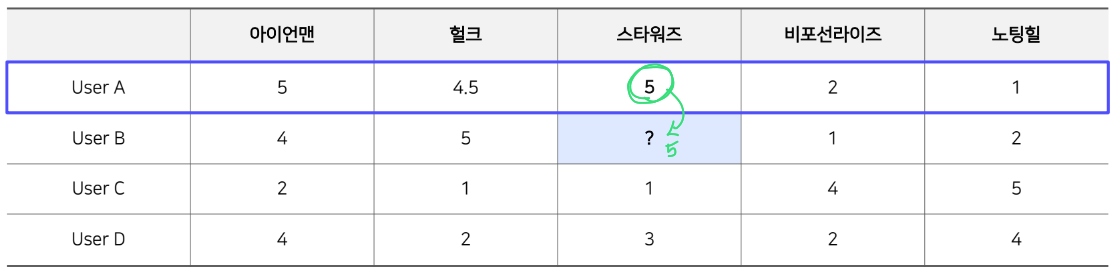
KNN 예시 ) 1-NN CF(K=1 인 경우)
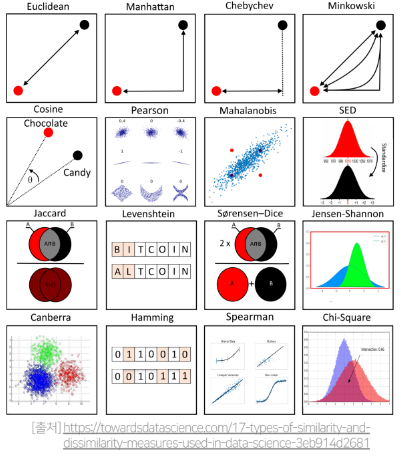
유사도 측정법 Similarity Measure
유사도 측정법이란 두 개체간의 유사성을 수량화하는 함수 혹은 척도이다.거리의 역수 개념을 사용 한다.
따라서 두 개체 간 거리를 어떻게 측정하냐에 따라서 유사도 측정법이 달라진다.
이렇게 다양한 유사도측정법이 있지만 여기서는 4가지 유사도 측정법을 알아보도록 하자.
※ 유사도는 딱 정해진 것이 없다. 우리가 가진 데이터와 서비스의 특징을 고려하고, Off-line Test에서 가장 좋은 유사도를 선택하는 것이 일반적이다.
Mean Squered Difference Similarity
Mean Squered Difference Similarity 는 주어진 user-item rating에 대해서 다음과 같이 계산한다.
m s d ( u , v ) = 1 ∣ I u v ∣ ⋅ ∑ i ∈ I u v ( r u i − r v i ) 2 , msd sim ( u , v ) = 1 m s d ( u , v ) + 1 m s d ( i , j ) = 1 ∣ U i j ∣ ⋅ ∑ u ∈ U i j ( r u i − r u j ) 2 , msd sim ( i , j ) = 1 m s d ( i , j ) + 1 \begin{array}{ll} msd(u, v)=\frac{1}{\left|I_{u v}\right|} \cdot \sum_{i \in I_{u v}}\left(r_{u i}-r_{v i}\right)^{2}, \quad \operatorname{msd}_{ \operatorname{sim}(u, v)}=\frac{1}{m s d(u, v)+1} \\ m s d(i, j)=\frac{1}{\left|U_{i j}\right|} \cdot \sum_{u \in U_{i j}}\left(r_{u i}-r_{u j}\right)^{2}, \quad \operatorname{msd}_{\operatorname{sim}(i, j)}=\frac{1}{m s d(i, j)+1} \end{array} m s d ( u , v ) = ∣ I u v ∣ 1 ⋅ ∑ i ∈ I u v ( r u i − r v i ) 2 , m s d s i m ( u , v ) = m s d ( u , v ) + 1 1 m s d ( i , j ) = ∣ U i j ∣ 1 ⋅ ∑ u ∈ U i j ( r u i − r u j ) 2 , m s d s i m ( i , j ) = m s d ( i , j ) + 1 1 수식을 간단히 해석해 보면 유저 or 아이템 끼리 비교 했을 때 두 평점을 빼준 값들의 평균이다.
Mean Squered Difference Similarity 는 거의 추천시스템에서만 쓰이는 유사도이다.
각 기준에 대한 점수의 차이를 계산하기 때문에 유사도는 유클리드 거리에 반비례 한다.
Cosine Similarity
이전 글(TF-IDF) 에서 다룬 것과 동일하게 적용한다.
cos ( θ ) = cos ( X , Y ) = X ⋅ Y ∣ X ∣ ∣ Y ∣ = ∑ i = 1 N X i Y i ∑ i = 1 N X i 2 ∑ i = 1 N Y i 2 \cos (\theta)=\cos (\mathrm{X}, \mathrm{Y})=\frac{\mathrm{X} \cdot \mathrm{Y}}{|\mathrm{X}||\mathrm{Y}|}=\frac{\sum_{i=1}^{N} X_{i} Y_{i}}{\sqrt{\sum_{i=1}^{N} X_{i}^{2}} \sqrt{\sum_{i=1}^{N} Y_{i}^{2}}} cos ( θ ) = cos ( X , Y ) = ∣ X ∣ ∣ Y ∣ X ⋅ Y = ∑ i = 1 N X i 2 ∑ i = 1 N Y i 2 ∑ i = 1 N X i Y i 벡터의 절대적 크기보다 각도를 중심으로 유사도를 측정하기 때문에 상대적인 유사도를 구하기 용이하다.
Pearson Similarity (=Pearson Correlation)
주어진 두 벡터 X,Y에 대하여
p e a r s o n _ s i m ( X , Y ) = ∑ i = 1 N ( X i − X ˉ ) ( Y i − Y ˉ ) ∑ i = 1 N ( X i − X ˉ ) 2 ∑ i = 1 N ( Y i − Y ˉ ) 2 { pearson\_sim }(\mathrm{X}, \mathrm{Y})=\frac{\sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{\sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{\sum_{i=1}^{N}\left(Y_{i}-\bar{Y}\right)^{2}}} p e a r s o n _ s i m ( X , Y ) = ∑ i = 1 N ( X i − X ˉ ) 2 ∑ i = 1 N ( Y i − Y ˉ ) 2 ∑ i = 1 N ( X i − X ˉ ) ( Y i − Y ˉ ) 각 벡터를 표본 평균으로 정규화한 뒤 코사인 유사도를 구한 값이다.
1에 가까울수록 양의 상관관계
0은 서로 독립
-1에 가까울스록 음의 상관관계
코사인 유사도와 다른 점은 정규화를 했다는 것인데, 이는 Rating의 크기를 고려한 것으로 해석할 수 있다.
Jaccard Similarity
Jaccard Similarity는 Cosine,Pearson유사도와 달리 집합의 개념을 사용한 유사도이다.
J ( A , B ) = ∣ A ∩ B ∣ ∣ A ∪ B ∣ = ∣ A ∩ B ∣ ∣ A ∣ + ∣ B ∣ − ∣ A ∩ B ∣ J(A, B)=\frac{|A \cap B|}{|A \cup B|}=\frac{|A \cap B|}{|A|+|B|-|A \cap B|} J ( A , B ) = ∣ A ∪ B ∣ ∣ A ∩ B ∣ = ∣ A ∣ + ∣ B ∣ − ∣ A ∩ B ∣ ∣ A ∩ B ∣ Jaccard 유사도의 특징은 집합을 사용했기 때문에 Cosine,Pearson유사도와 달리벡터의 차원이 달라도 이론적으로 유사도 계산이 가능하다는 점이다.
두 집합이 가진 아이템이 모두 같으면 1
두 집합이 겹치는 아이템이 하나도 없으면 0
Jaccard 유사도 예시u A u_A u A u B u_B u B
u 4 : m 1 , m 3 u B : m 2 , m 3 , m 4 . J ( A , B ) = ⌊ { m 1 , m 3 } ∣ ∣ { m 1 , m 3 , m 4 ∣ ∣ = 2 3 \begin{aligned} &u_{4}: m_{1}, m_{3} \\ &u_{B}: m_{2}, m_{3}, m_{4} . \\ & J(A, B)=\frac{\left\lfloor\left\{m_{1}, m_{3}\right\} \mid\right.}{\mid\left\{m_{1}, m_{3}, m_{4}||\right.} \\ &=\frac{2}{3} \end{aligned} u 4 : m 1 , m 3 u B : m 2 , m 3 , m 4 . J ( A , B ) = ∣ { m 1 , m 3 , m 4 ∣ ∣ ⌊ { m 1 , m 3 } ∣ = 3 2