이 글은 부스트캠프 AI Tech 3기 강의를 듣고 정리한 글입니다.
개요
이 글에 다루는 Rating Prediction은 User-based CF 를 기준으로 설명을 진행한다.
Collaborative Filtering 의 최종목적은 평점을 예측하는 것이다.
CF의 목적에서 헷갈리지 않아야 하는게 있는데 CF는 최종 추천은 하지 않는다는 점이다.
RecSys의 최종목적은 예측평점이 높은 아이템을 유저에게 추천하는 것이고, 그 과정중에 CF가 있음을 유의하도록 하자.
CF를 이용한 추천의 간단한 프로세스
CF로 예측평점을 계산
타겟 유저에 대한 아이템의 예측 평점을 높은 순 정렬하여 Top N개 추천
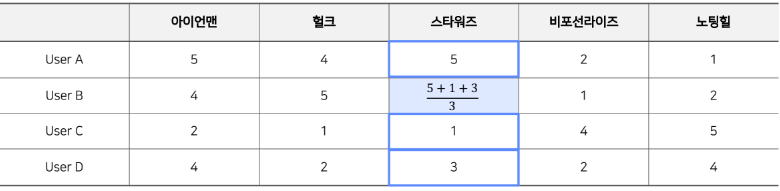
Absolute Rating
Absolute Rating은 다른 유저들의 평가를 단순평균이나 가중평균으로 구하는 방식이다.
Average
r ^ ( u , i ) = ∑ u ∈ ∈ Ω i r ( u ′ , i ) ∣ Ω i ∣ \hat{r}(u, i)=\frac{\sum_{u \in \in \Omega_{i}} r\left(u^{\prime}, i\right)}{\left|\Omega_{i}\right|} r ^ ( u , i ) = ∣ Ω i ∣ ∑ u ∈ ∈ Ω i r ( u ′ , i ) 다른 유저들의 해당 영화(스타워즈)에 대한 단순평균을 낸 것이다.
r ^ B i = 5 + 1 + 3 3 \hat r_{Bi} = \frac{5+1+3}{3} r ^ B i = 3 5 + 1 + 3 이때 문제점은 유저 B입장에서 유저 A,C,D 의 rating을 동일하게 반영하여 제대로된 평가 예측이 어렵다는 점에 있다.
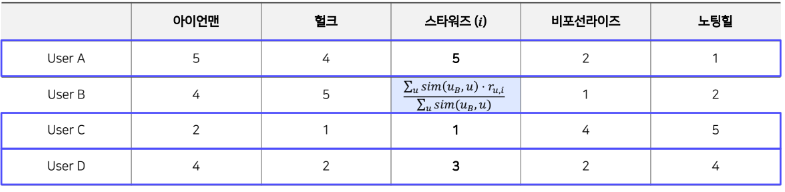
Weighted Average
r ^ ( u , i ) = ∑ u ′ ∈ Ω i sim ( u , u ′ ) r ( u ′ , i ) ∑ u , ∈ Ω i sim ( u , u ′ ) \hat{r}(u, i)=\frac{\sum_{u \prime \in \Omega_{i}} \operatorname{sim}\left(u, u^{\prime}\right) r\left(u^{\prime}, i\right)}{\sum_{u, \in \Omega_{i}} \operatorname{sim}\left(u, u^{\prime}\right)} r ^ ( u , i ) = ∑ u , ∈ Ω i s i m ( u , u ′ ) ∑ u ′ ∈ Ω i s i m ( u , u ′ ) r ( u ′ , i ) Average의 문제점은 평점 예측시 유사도가 낮은 유저의 영향을 유사도가 높은 유저의 영향과 동일하게 받는다는 점이었다.
Weighted Average는 이를 해결하기 위해 유저의 유사도를 이용하여 가중평균을 구하는 것이다.
r ^ B i = 0.95 ⋅ 5 + 0.6 ⋅ 1 + 0.85 ⋅ 3 0.95 + 0.6 + 0.85 = 3.3 \hat r_{Bi} =\frac{0.95 \cdot 5+0.6 \cdot 1+0.85 \cdot 3}{0.95+0.6+0.85}=3.3 r ^ B i = 0 . 9 5 + 0 . 6 + 0 . 8 5 0 . 9 5 ⋅ 5 + 0 . 6 ⋅ 1 + 0 . 8 5 ⋅ 3 = 3 . 3 어느정도 문제가 해결된 것 같지만 사실 한가지 문제점이 남아있다.
Relative Rating
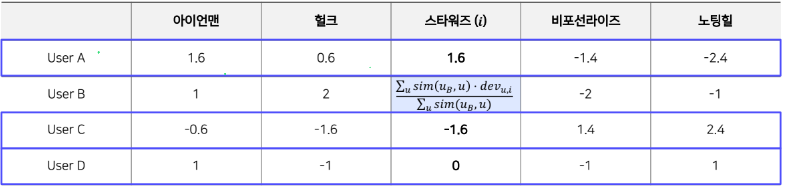
dev ( u , i ) = r ( u , i ) − r u ‾ f o r k n o w n r a t i n g \operatorname{dev}(u, i)=r(u, i)-\overline{r_{u}} \quad for known rating d e v ( u , i ) = r ( u , i ) − r u f o r k n o w n r a t i n g 위의 문제점(유저간 편차)를 해결하기 위한 아이디어는 각 유저의 평균 평점을 각 유저가 평가한 평점에 빼주는 것이다.
이렇게 하면 각 유저마다 높게 평가한 영화가 두드러질 것이고, 긍정적, 부정적 유저에 대한 문제점이 어느정도 해소된다.
dev ^ ( u , i ) = ∑ w ∈ Ω i dev ( u ′ , i ) ∣ Ω i ∣ = ∑ u ′ ∈ Ω i r ( u ′ , i ) − r w ‾ ∣ Ω i ∣ \widehat{\operatorname{dev}}(u, i)=\frac{\sum_{w \in \Omega_{i}} \operatorname{dev}\left(u^{\prime}, i\right)}{\left|\Omega_{i}\right|}=\frac{\sum_{u \prime \in \Omega_{i}} r\left(u^{\prime}, i\right)-\overline{r_{w}}}{\left|\Omega_{i}\right|} d e v ( u , i ) = ∣ Ω i ∣ ∑ w ∈ Ω i d e v ( u ′ , i ) = ∣ Ω i ∣ ∑ u ′ ∈ Ω i r ( u ′ , i ) − r w 이제 모든 평점 데이터를 dev ( u , i ) \operatorname{dev}(u, i) d e v ( u , i )
r ^ ( u , i ) = r u ‾ + ∑ u ∈ Ω i r ( u ′ , i ) − r u r ‾ ∣ Ω i ∣ = r u ‾ + dev ^ ( u , i ) \hat{r}(u, i)=\overline{r_{u}}+\frac{\sum_{u \in \Omega_{i}} r\left(u^{\prime}, i\right)-\overline{r_{u r}}}{\left|\Omega_{i}\right|}=\overline{r_{u}}+\widehat{\operatorname{dev}}(u, i) r ^ ( u , i ) = r u + ∣ Ω i ∣ ∑ u ∈ Ω i r ( u ′ , i ) − r u r = r u + d e v ( u , i ) 그리고 예측한 deviation을 타겟 유저 평균 rating과 더해주면 최종 예측 평균을 구할 수 있게 된다.
Relative Rating 예시다음의 표를 deviation을 반영한 matrix라고 가정하고 User B의 스타워즈의 예측 평점을 구해보도록 하자
dev ^ ( u , i ) \widehat{\operatorname{dev}}(u, i) d e v ( u , i )
dev ^ ( u , i ) = 1.6 ⋅ 0.95 + ( − 1.6 ) ⋅ ( 0.6 ) + 0 ⋅ 0.85 0.95 + 0.6 + 0.85 = 0.23 \widehat{\operatorname{dev}}(u, i) = \frac{1.6 \cdot 0.95+(-1.6) \cdot(0.6)+0 \cdot 0.85}{0.95+0.6+0.85}=0.23 d e v ( u , i ) = 0 . 9 5 + 0 . 6 + 0 . 8 5 1 . 6 ⋅ 0 . 9 5 + ( − 1 . 6 ) ⋅ ( 0 . 6 ) + 0 ⋅ 0 . 8 5 = 0 . 2 3
dev ^ ( u , i ) \widehat{\operatorname{dev}}(u, i) d e v ( u , i )
r ^ ( u , i ) = 0.23 + 3 = 3.23 \hat{r}(u, i) = 0.23 + 3 =3.23 r ^ ( u , i ) = 0 . 2 3 + 3 = 3 . 2 3 IBCF 는 유저->아이템으로 관점을 바꿔 동일한 Task를 진행해주면 된다.

잘 배우고 갑니다 감사합니다