이번에는 이전글에서 다룬 Epsilon-Greedy나 UCB보다 발전된 기법으로 현업에서 자주 사용되는 MBA 알고리즘인 Thompson sampling과 LinUCB를 알아보자.
Thompson Sampling
Thompson Samping은 주어진 K개의 action에 해당하는 확률 분포를 구하는 문제로 action 에 해당하는 reward 추정치인 를 계산 할 때 확률 분포를 따른다고 가정하고 그 추정치를 계속 업데이트 하는 방법이다. 특히 베타분포를 많이 사용한다.
베타분포
베타 분포는 두개의 양의 변수로 표현할 수 있는 확률 분포로 0과 1사이 값을 갖는다.
이때 는 에 의해 정해지는 베타함수 이다.
Thompson sampling 예시
사용자에게 보여줄 수 있는 광고 배너가 있다고 가정하자.
이때 우리의 목표는 어떤 베너를 노출했을 때 가장 많은 클릭을 얻어낼지 예측해서 추천해주는 것이고 이를 위한 Policy를 정해주는 것이 해야할 Task 가 된다.
우선 베타분포에 필요한 데이터 2가지를 정의한다.
- : 배너를 보고 클릭한 횟수
- : 배너를 보고 클릭하지 않은 횟수
알파와 베타를 정의하였으면 확률분포를 정의 해보자.
- : 우리가 가정한 베타분포
를 따른다고 가정하였기 때문에 베타분포에서 샘플링한 값이 최종적으로 베너를 클릭할 확률이라고 생각하자.
Thompson Sampling은 다음의 과정을 거친다.
- 데이터가 없는 초기상태 - 최초의 사전확률 분포로 동일한 값으로 설정
- 일정기간동안 랜덤하게 노출 - 어느정도 관측값들을 수집해서 베타 분포를 적절한 수준까지 업데이트 하기 위함
- 베타 분포에서 샘플링하여 노출 - 어느정도 데이터가 모이면 Thompson Sampling 의 Policy 사용
- 과정 3을 통해 수많은 노출을 거친 후 수렴한 reward 중 가장 높은 reward 기대값을 가지는 아이템 추천
<-> 만약 Thompson sampling이 아닌 Greedy 알고리즘을 사용한다면 과정 3부터 표본 평균이 가장 높은 것을 선택하여 추천했을 것이다.
과정을 예시 그림으로 살펴보자.
Step1. : 데이터가 없는 초기상태 - 최초의 사전확률 분포로 동일한 값으로 설정
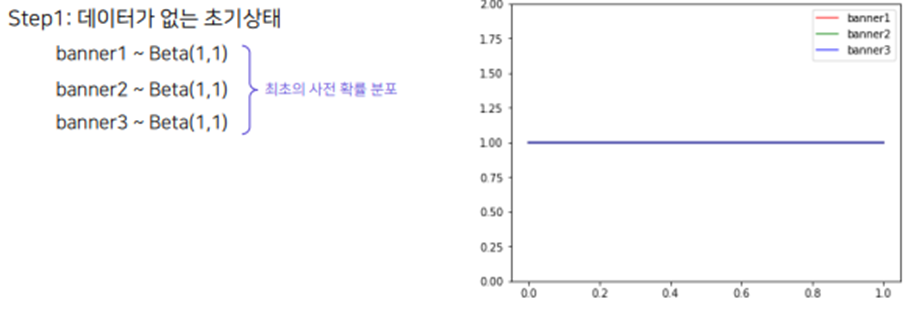
Step2. : 어느정도 관측값들을 랜덤하게 수집해서 베타 분포를 적절한 수준까지 업데이트
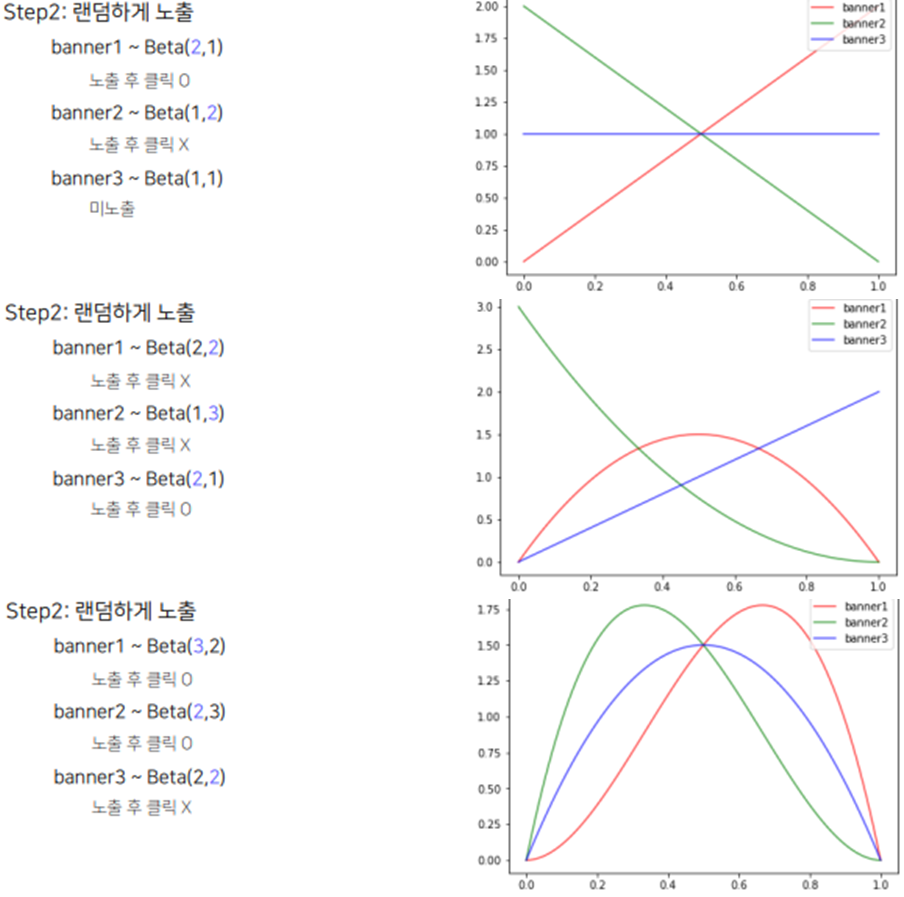
Step3. : 이제 랜덤 샘플링을 하지 않고 Thompson sampling진행(베타 분포에서 샘플링)하여 각 베너별 베타 분포를 업데이트
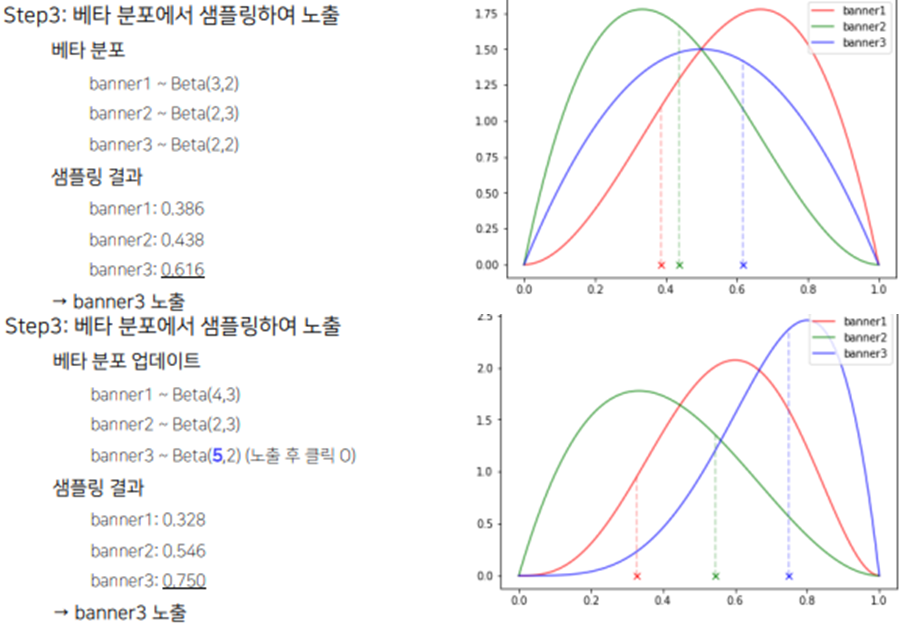
Step4. 수많은 노출을 거친 후 베타분포가 뾰족해졌을 때(True 값에 수렴) 최대 reward를 기대값으로 갖는 베너를 선택하여 추천해 준다.
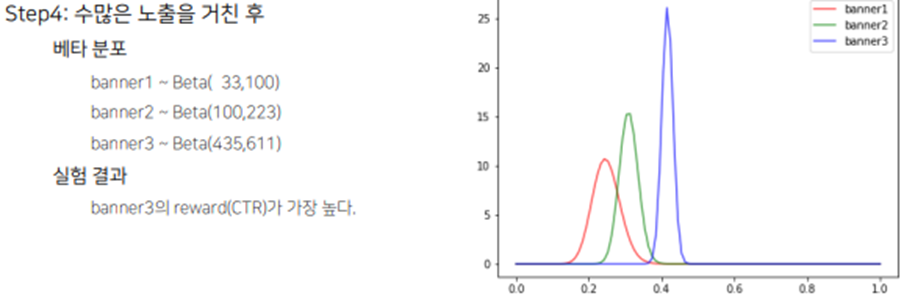
이러한 과정을 통해 Exploitation과 Exploration이 확률 분포를 따라서 적절한 Trade-off를 유지하면서 다양한 아이템이 노출되다가 가장 reward가 높은 아이템을 노출하는 것으로 수렴하는 결과를 얻을 수 있다.
Pseudo Code로도 한번 살펴보자.
# Algorithm 2 Thompson sampling for the Bernoulli bandit
Require: α, β prior parameters of a Beta distribution
Si = 0, Fi = 0, ∀i. {Success and failure counters} # α, β 를 두고 Beta 분포를 초기화
for t = 1, . . . , T do # 매 timestep마다
for i = 1, . . . , K do # K개의 액셔ㅑㄴ에 대해서 각각
Draw θi according to Beta(Si + α, Fi + β). # 베타분포를 셈플링하고
end for
Draw arm ˆı = arg maxi θi and observe reward r #샘플링한 θi중 가장 큰 Sampling 값을 가진 액션을 선택
if r = 1 then # 클릭이 일어나면
Sˆı = Sˆı + 1 # 앞에 Beta 분포값을 업데이트
else # 클릭을 안한다면
Fˆı = Fˆı + 1 # 뒤에 Beta 분포값을 업데이트
end if
end for
Lin UCB
Contextual Bandit
우선 Contextual Bandit이 무엇인지 알아보자.
앞선 글에서 Context 란 id 외의 feature(유저의 데모그래픽, 아이템 카테고리, 태그)로 정의 하였다.
Bandit에도 이렇게 Context 정보를 활용한 방법과 활용하지 않은 방법이 있다.
-
Context-free Bandit
동일한 action에 대해 유저의 context 정보에 관계없이 항상 동일한 reward를 가진다고 가정하고 모델링하는 방법으로 사람이 달라진다고 슬롯머신 reward 확률이 달라지지 않는다는 관점이다.
ex ) UCB, Epsilon Greedy -
Contextual Bandit
유저의 Context 정보에 따라 동일한 action이더라도 다른 reward를 가진다. 예를들어 동일한 스포츠 기사를 보더라도 나이나 성별에 따라 클릭 성향이 다르다고 볼 수 있기 때문이다. 이는 개인화 추천과도 연관이 있다.
LinUCB
이제 LinUCB를 알아보자.
Arm-selection Strategy : 액션 선택을 위한 Policy 수식
-
-차원 컨텍스트 벡터로 user와 context에 대한 feature가 사용됨
(아이템을 노출시킬 유저의 성별, 연령, 노출되는 시간적 공간적 정보, 아이템의 부가적인 정보 등) -
: action 에 대한 -차원 학습 파라미터로 액션별로 가지는 파라미터이고 액션별로 데이터가 수집되면서 업데이트 됨
-
시점의 개의 컨텍스트 벡터(학습 데이터)로 구성된 행렬이다.
(현재 timestep 기준으로 총 m개의 Action 데이터가 수집되었다면 행렬)
첫번째 term 는 주어진 context 에서 Action a 를 선택시 받는 reward의 기대값이다. (Expected reward term)
두번째 term 은 그 action 에 대한 Exploration을 추가한 것으로 시간이 지나 학습데이터가 많이 수집되면 작아진다.(Exploration Term)
이렇게 수식은 학습데이터가 많아질수록 Exploration Term이 작아지면서 최종적으로 Expected reward에 수렴하게 되고 그 reward가 가장 높은 Action을 선택되는 쪽으로 Exploitation이 진행된다.
그림으로 알아보자.
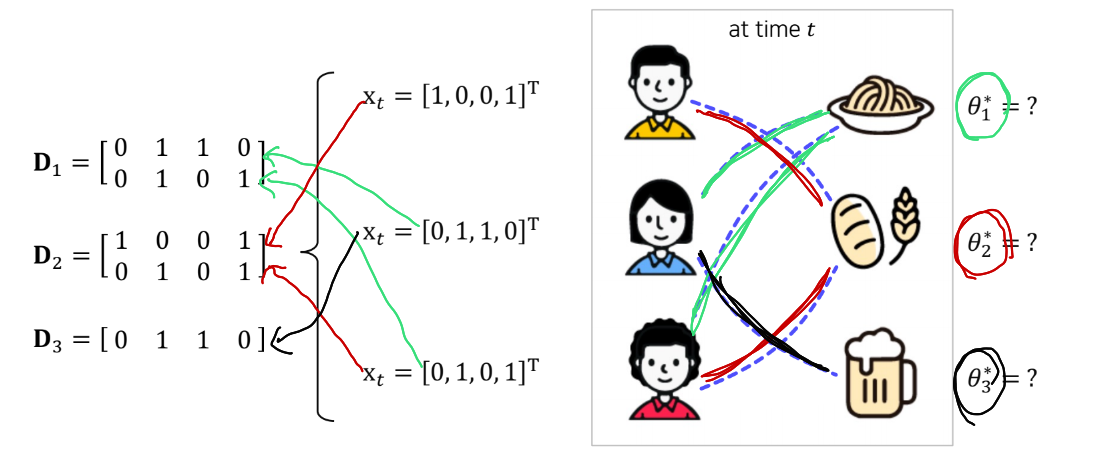
그림은 3명의 서로다른 Context를 가진 유저를 나타낸다.
여기서 는 각 유저의 Context Vector로 4차원으로 각 차원은 다음의 특성을 갖는다고 가정하자.
- 첫번째 차원 : male
- 두번째 차원 : female
- 세번째 차원 : young
- 네번째 차원 : old
그림의 유저에 대입해 보면 첫번째 유저의 Context Vector 는 male과 old의 특성을 가진다고 볼 수 있다.
이제 이 유저들이 어떤 아이템을 선택하는가가 MAB문제에서 추천이 되는 방식이다. 각각의 아이템(액션)에 대해서 학습해야 한다.
첫번째 유저는 빵을 좋아하고
두번째 유저는 파스타와 맥주
세번째 유저는 파스타와 빵을 좋아한다.
그렇다면 첫번째 액션에 해당하는 은 총 두명에게 수집이 되었기 때문에 으로 업데이트가 된다.
두번째 세번째 액션도 같은 방식으로 를 업데이트한다.
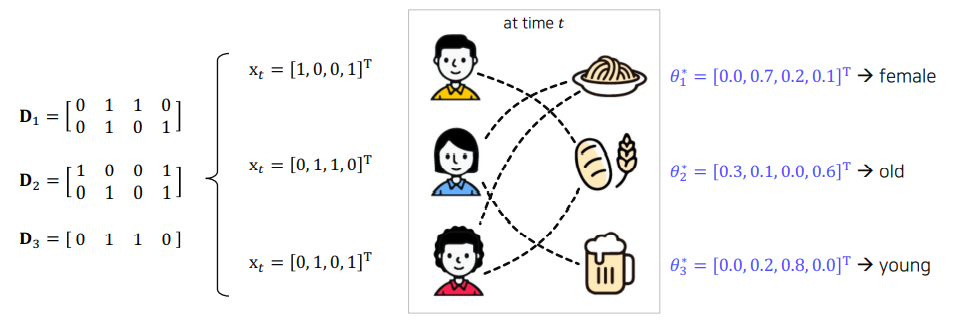
이렇게 학습을 하고 나면 그림과 같이 Context vector와 같은 차원의 벡터 들이 구해지게 된다.
첫번째 액션(파스타)의 파라미터는 두번째 차원이 가장 높은 weight를 가지는데 이는 female이라는 특성을 가진 유저에게 줄 수 있는 reward가 가장 크다고 학습한 것이다.
두번째(빵), 세번째(맥주)도 마찬가지로 각각 old, young의 특성을 가진 유저에게 높은 reward를 줄 것 이라고 학습한다.
이렇게 LinUCB는 각 유저의 context vector에 따라서 어떤 아이템이 더 높은 reward를 줄지(클릭율이 높을지) 보고 추천하도록 학습한다.
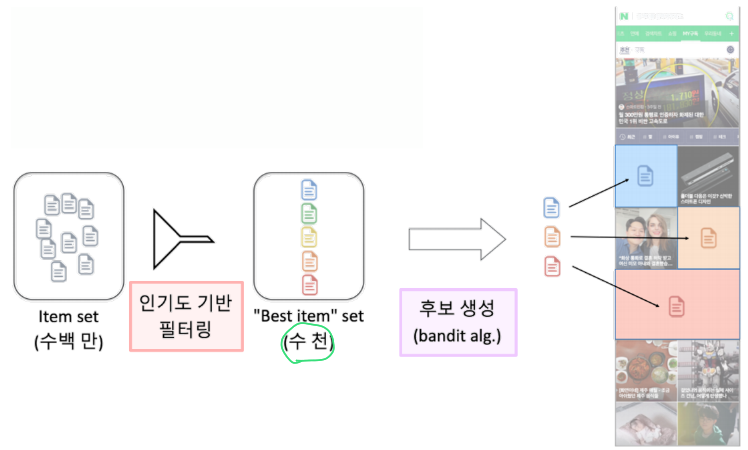
Contextual Bandit 예시 : Naver AiRs 추천 시스템
Bandit의 Action 하나하나가 item이 되는데 item이 너무 많은 경우 인기도 기반 필터링을 통해 탐색(exploration) 대상을 수천개로 축소한 뒤 Contextual Bandit 알고리즘을 통해 유저의 취향을 탐색 및 활용한다.