Multi-Armed Bandit (MAB) 이란?
※ Bandit의 개념은 원래 강화학습의 기초개념이지만, 간단하게 구현되기 때문에 현업에서도 종종 쓰인다.
MAB(Multi-Armed Bandit)가 추천시스템에 어떻게 적용되는지 알아보기 위해 우선 MAB가 무엇인지 알아보자.
카지노에 있는 슬릇머신을 생각해 보자.
슬릇머신은 한번에 한개의 arm(손잡이;레버)를 당길 수 있고 이에 대한 reward를 얻게된다. 이렇게 한번에 한개의 arm을 당기는 경우를 One-Armed Bandit이라고 표현하는데, 만약 카지노에 있는 K개의 슬릇 머신을 N번 플레이 할 수 있다고 한다면 어떻게 Reward를 많이 얻을 수 있을까라는 고민을 할 수 있게 되고, 이를 문제화 한 것이 Multi-Armed Bandit이다.
MAB는 K개의 슬롯머신에서 얻을 수 있는 reward의 확률이 모두 다르다고 가정을 하기 때문에 어떤 슬롯머신을 당겨야 어떤 순서나 정책(Policy)로 당겨야 최대의 reword를 얻을 수 있을지 학습하는 알고리즘이다.
즉 MAB를 통에 얻는 것은 어떤 정책(Policy)를 통해 reward를 얻을 것인가 이다.
MAB의 Challenge
MAB의 가장 큰 문제점이자 알고리즘적으로 해결해야 할 문제의 핵심은 슬롯머신의 reward 확률을 정확히 알 수 없다는 것이다.
우선 이를 해결하기 위한 간단한 MAB 정책(Policy) 2가지를 살펴보자.
-
모든 슬롯머신을 동일한 횟수로 당김
->가장 간단한 방법이지만 높은 reward를 받기 어렵다. -
일정횟수만큼 슬롯머신을 당겨보고 남은 횟수는 그 시간 동안 제일 높은 확률을 가진 슬롯머신만 당김
->동일한 슬롯만 계속 당기게 될 수 있다.
이 두가지 문제를 일반화하면 Exploration 과 Exploitation 의 Trade-off 관계라고 볼 수 있다.
-
Exploration(탐색)
더 많은 정보를 얻기 위해 새로운 arm을 선택하는 것으로 다양한 슬롯머신을 돌리면서 정확한 예측값을 얻는 것이다. Exploration만 하게 된다면(탐색에 너무 많은 비용을 쓴다면) reward를 많이 받을 수 없게 된다. -
Exploitation(활용)
기존의 경험이나 관측값을 토대로 가장 좋은 arm을 선택하는 것으로 reward를 많이주는 슬롯머신을 찾으면 그것만 당기는 것을 말한다. 이때 만약 충분한 데이터를 가지지 못한 채로 reward를 많이주는 슬롯머신을 잘못 선택했을 경우 최종 reward는 적어지게 된다(높은 reward를 보장할 수 없다).
따라서 Exploration과 Exploitation의 Trade-off를 적절히 고려한 Policy를 수립하여 최대 reward를 얻는 것이 MBA의 핵심이라 볼 수 있다.
MBA Formula
MBA의 기본적인 수식은 다음과 같다.
- : time step or playnumber (몇번째로 당겼는가를 의미)
- : 시간에 선택한 action
- : 시간에 받은 reward
- : 최종적으로 알고 싶은 값으로 액션 에 따른 reward의 실제 기대값
만약 우리가 모든 액션에 대해 을 정확히 알고 있다면 기대값이 가장 큰 액션만 돌리면 되기 때문에 문제를 쉽게 해결 할 수 있게 된다.
하지만 우리는 실제 reward의 true distirbution을 모르기 때문에 이를 추정하여 구하게 된다.
따라서 에 대한 시간 에서의 추정치 를 최대한 와 비슷하게 구하는 것이 MBA의 목표가 된다.
MAB 기초 알고리즘 3가지
Greedy Algorithm
MAB 문제에서 Greedy Algorithm이란 를 구하기 위해 액션에서 얻은 리워드의 단순평균을 사용한다.
지금까지 관측된 개별 머신 reward의 표폰평균을 구하는데 수식은 다음과 같다.
여기서 분자는 t-1시점까지 a액션을 했을 때 얻은 reward의 총합이고, 분모는 t-1시점까지 a 액션이 선택된 수행횟수이다.
Greedy Algorithm은 가장 간단한 Policy로 평균 리워드가 최대인 action을 선택하는 것이다.
이 수식에서 는 reward가 수집되면서 계속 업데이트하게 되고 리워드가 가장 큰 action을 선택하게 된다.
문제는 처음에 선택되는 action이 원래 좋은 reward를 주다가 운이 않 좋아 낮은 reward를 줬다면, 그 action의 reward 평균이 낮기 때문에 다시는 선택될 기회조차 사라지는 문제점이 발생한다 (Exploration이 부족)
Epsilon Greedy
Exploration이 부족한 greedy algorithm의 Policy를 수정한 전략이다.
eplsilon()의 일정한 확률로 greedy 하게 선택할지 랜덤하게 선택할지를 결정한다.
수식은 다음과 같다.
epsilon-greedy는 Exploration과 Exploitation을 모두 고려한 기법으로 심플하면서도 강력한 알고리즘이기 때문에 MAB 비교시 베이스로 많이 사용된다.
epsilon-greedy의 단점은 데이터가 많이 쌓여 True disribution을 측정했더라도, 항상 epsilon의 확률로 랜던하게 선택하기 때문에 후반에는 손해를 많이 보게 된다.
UCB : User Confidence Bound
UCB은 시간이 지날수록 exploitaion을 증가시키는 방식의 알고리즘으로 수식은 다음과 같다.
- : 관측값에서 action 를 선택했던 횟수
- : exploration을 조정하는 하이퍼파라미터
는 앞선 greedy에서 본 표본평균을 사용하게 되는데 달라지는 점은 뒤에 붙은 이다.
수식을 해석해 보면 시간이 지나면서 모든 액션에 대한 가 선형적으로 증가하고, 는 함수라서 뒤로 갈수록 증가하지 않게 된다. 즉 후반에는 점점 0으로 수렴하게 되어 데이터가 충분히 쌓였다면 지금까지 구해진 표본 평균 리워드로 최종 exploitation을 진행하게 된다는 것이다.
이 term은 초반에는 분모가 작아서 불확실성이 커지고 결국 가 커지게 되어 해당 action이 선택될 확률이 높아진다.
이는 자연스럽게 exploration에서 exploitatio으로 policy의 변화를 가져다 주게 된다.
다음의 그래프는 지금까지 알아본 알고리즘들의 하이퍼파라미터에 따른 reward 값을 나타낸다.
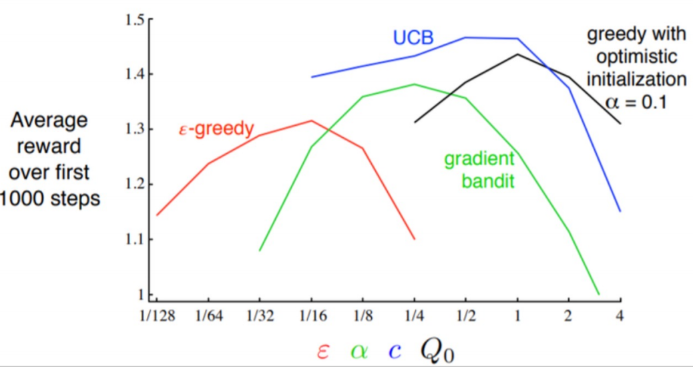
그래프에서 볼 수 있듯이 모두 거꾸로된 U자형태를 하고있다.
이는 MAB에서 적절한 하이퍼파라미터를 찾아 exploration과 exploitation이 적절히 Trade-off가 되려된 Optimal point를 찾아야 한다고 볼 수 있다.
MAB 적용 예시
MAB를 이용한 추천 시스템
기존 추천 시스템은 다음과 같이 추천을 하였다.
- 유저에게 Top-N개의 아이템을 추천
- 주어진 아이템과 유사한 아이템을 추천
이를 Bandit 문제로 바꾼다면 완전히 다른 접근을 할 수 있게된다.
기존의 추천은 평점, 유사도를 사용하였지만, Bandit문제로 풀게 된다면 실제 서비스의 지표인 클릭/구매를 모델의 reward로 가정하여 reward를 최대화 하는 방향으로 모델이 학습되고 추천을 수행한다.
실제로도 무거운 추천 모델을 사용하지 않고 간단한 Bandit 기법을 적용하여도 온라인 지표(CTR, CVR)이 좋아지는 현상이 있다.
MAB를 이용하여 추천을 하게 된다면 action과 reward를 추천에 맞게 정의해주어야 한다.
우리가 추천하는 개별 아이템은 개별 action으로 볼 수 있고, 아이템을 추천했을 때 사용자의 클릭여부(binary)를 reward로 측정한다.
이때 우리가 유저에게 아이템이 추천하는 방식을 MAB 알고리즘의 Policy로 설정하면 추천문제를 MAB를 이용하여 풀 수 있게 된다.
MAB에서 중요한 개념인 exploration 과 exploitation도 추천 문제에 맞춰보면 다음과 같다.
- exploration
지속적으로 변화하는 유저의 취향 탐색 및 추천 아이템 확장( 정보를 얻는 행위 ) - exploitation
유저 취향에 맞는 아이템 추천
MAB는 구현이 간단하고 이해가 쉬운 장점이 있어 실제 비즈니스에 매우 유용하다.
유저 추천
개인별로 Bandit을 구축하기에는 데이터가 부족하고 한계가 있어 개인마다 아이템 하나하나의 Bandit을 구성하기 위해서는 굉장히 많은 Bandit이 필요하게 되고 수렴하지 않는 문제가 있다.
따라서 클러스터링을 통해 비슷한 유저끼리 그룹화한 뒤 해당 그룹 내에서 Bandit을 구축하는 방법을 사용한다.
즉 클러스터 별로 아이템 후보 리스트를 생성하는데 이때는 인기도 기반, CF 기반 방법 등 다양한 방법을 이용한다.
최종적으로 필요한 Bandit의 개수는 유저클러스터 개수 X 후보아이템 개수 가 된다.
그림을 통해 알아보자.
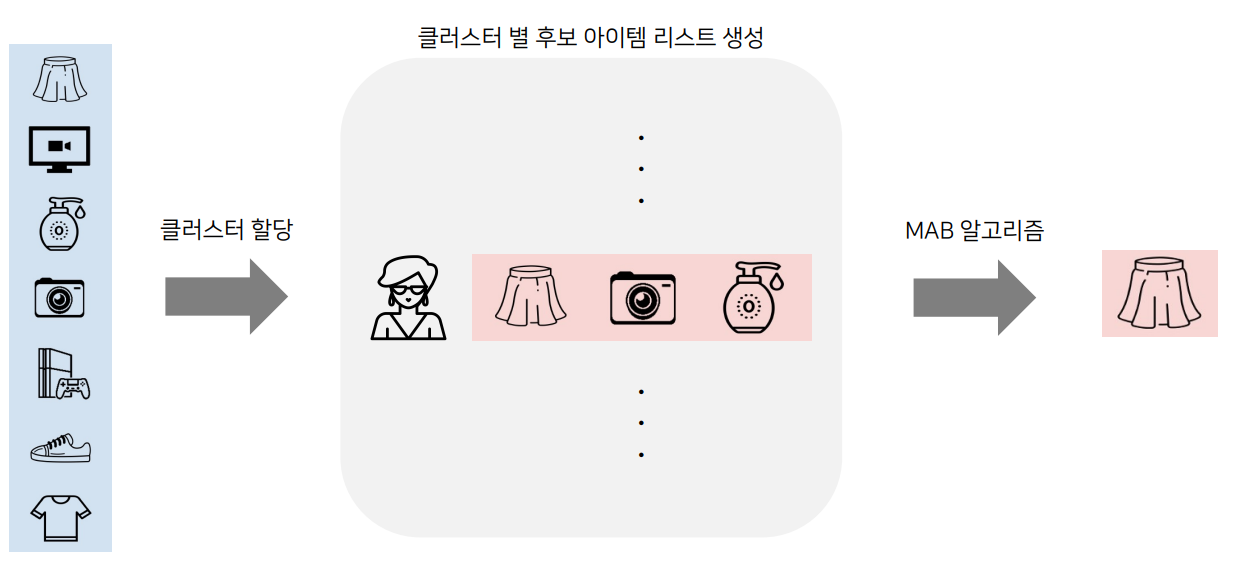
다양한 아이템들이 있다고 하면 이 아이템들을 각각의 유저 클러스터에 할당을 한다.
그리고 특정 유저가 들어왔을 때 유저의 클러스터를 찾고, 클러스터에 후보 아이템이 3개(치마,카메라, 로션) 있다고 했을 때 이 3개의 아이템에 대해서 MAB알고리즘을 적용하여 어떤 아이템을 선택시 reward가 클지(클릭을 많이 할지) 계산하여 최종적인 아이템(치마)를 추천해 주게 된다.
유사 아이템 추천
유사 아이템 추천은 유저추천과 같은 이유(아이템마다 Bandit 생성 불가능)로 인해 주어진 아이템과 유사한 후보 아이템 리스트를 생성하고 그 안에서 Bandit을 적용한다.
이때 유사 아이템을 추출하는 방법은 user-item interaction을 기반으로 한 유사도(MF, item2vec 등)를 사용하거나 Content-based 유사도를 구하여 후보 아이템 리스트를 생성한다.
최종적으로 필요한 Bandit의 개수는 아이템 개수 X 후보 아이템 개수 가 된다.
이떄 후보리스트는 전체 리스트보다 훨씬 작은 리스트 크기를 가진다.
그림으로 알아보자.
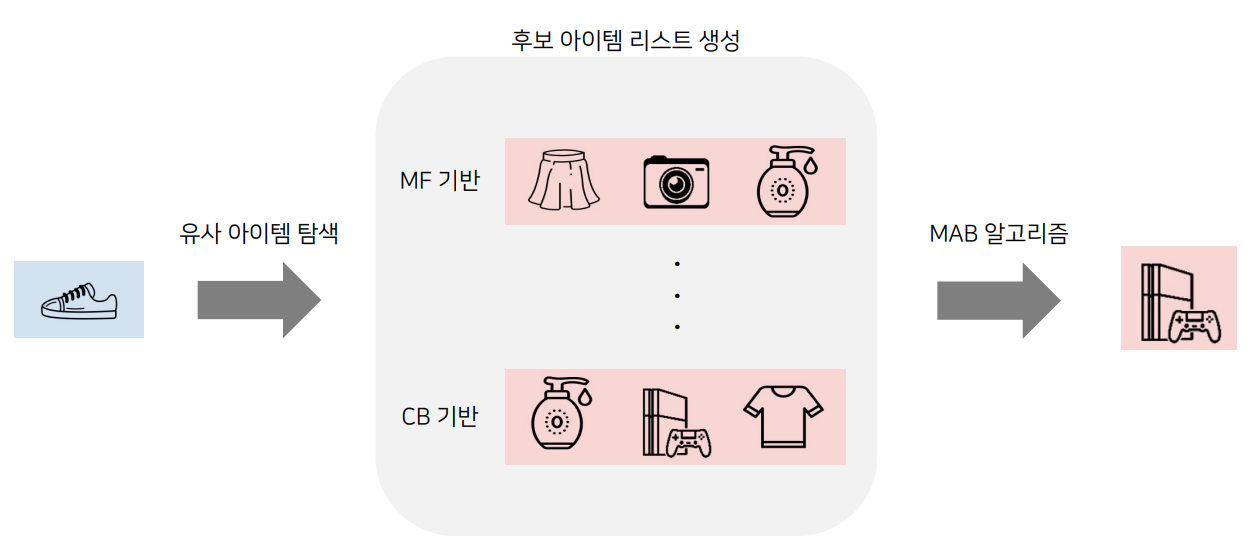
신발아이템이 소개된 홈페이지에 방문했다고 가정을 해보자.
그럼 신발과 유사한 아이템을 탐색하는데 이때 후보 아이템 생성은 MF 기반 유사도를 사용하거나(치마, 카메라, 로션) , CB기반 유사도를 사용하여(로션,PS5,티셔츠)유사한 후보 아이템 리스트를 생성한다.
그리고 MBA 알고리즘을 이용하여 최대 reward를 받을 아이템(PS5)를 추천한다.
유저추천이나 유사 아이템 추천해주는 케이스는 방식이 정해진 것이 아니라 하나의 예시일 뿐이다. 서비스에 맞게, 적용방식에 맞게 후보 아이템 리스트를 생성하고 여기에 MAB를 적용하여 추천하는 서비스는 다양하게 변화시켜 적용이 가능하다.
