이 글은 부스트캠프 AI Tech 3기 강의를 듣고 정리한 글입니다.
딥러닝에서 왜 확률론이 필요한가?
기계학습에서 사용되는 손실함수(Loss Function)들의 작동원리는 데이터 공간을 통계적으로 해석해서 유도함
- 컴퓨터로 수식을 해석적으로 계산하는 것은 힘들기 때문에
- 딥러닝 또한 확률론 기반의 기계학습이론에 바탕을 두고 있다
이에 대한 예시로 몬테카를로 샘플링을 들 수 있다.
몬테카를로 샘플링(Monte Carlo Sampling)
- 기계학습의 많은 문제들은 확률분포를 명시적으로 모를 때가 대부분이다.
- 확률분포를 모를 때 데이터를 이용하여 기대값을 계산하려면 몬테카를로 샘플링을 이용해야한다.
- 몬테카를로 샘플링은 독립 추출만 보장된다면 대수의 법칙에 의해 수렴성을 보장한다.
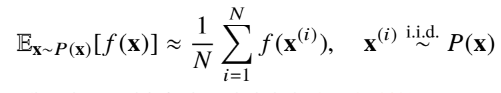
쉽게 말해 독립적으로 샘플링한 것들의 기대값은 구하고자 하는 와 유사해지게 된다는 것이다.
by Python Code
코드로 보면 이해하기 쉬운데

-1~1까지의 적분값을 몬테카를로 샘플링으로 근사하는 코드이다.
import numpy as np
def mc_int(fun, low, high, sample_size=100, repeat=10):
int_len = high-low # 적분 범위
stat = []
for _ in range(repeat):
# 균등분포로 sample_size만큼 [-1, 1] 구간의 x값을 추출한다.
x = np.random.uniform(low=low, high=high, size=sample_size)
# 추출된 이x값으로 높에 해당하는 함수 값을 계산한다.
fun_x = fun(x)
# 밑변과 높이를 곱해 넓이인 int_val을 계산한다.
int_val = int_len * np.mean(fun_x)
stat.append(int_val)
# 구해진 통계량(넓이)를 평균내주면 실제 값과 거의 근사한다.
return np.mean(stat), np.std(stat)
def f_x(x):
return np.exp(-x**2)
print(mc_int(f_x, -1, 1, 10000, 100))
# 결과
# (1.4939731002894978, 0.003764717448739865