이 글은 부스트캠프 AI Tech 3기 강의를 듣고 정리한 글입니다.

개요

딥러닝은 신경망[선형모델 / 활성함수]의 여러층에 대한 합성함수이기 때문에

목적식(손실함수)의 gradient 계산을 위해 연쇄법칙을 적용한 역전파를 사용한다.

신경망을 분해

신경망은 기본적으로 선형모델이 아닌 비선형 모델이다.

신경망을 수식적으로 분해해 보면 선형모델과 활성화함수로 이루어져 있다

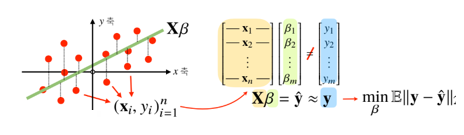
목적식(참값 - 추정값)의 크기를 가장 작게 만들어 주는 $\beta$를 찾았다.

하지만 단순히 선형변환만을 통해서는 복잡한 모델을 설명할 수 없다.

따라서 기존 선형 변환에 비선형 변환을 합성하여복잡한 모델을 설명 할 수 있게 한다. -> 신경망

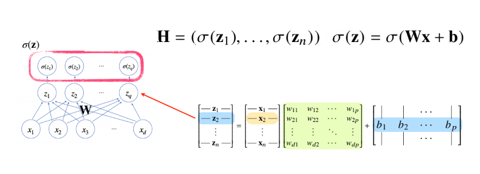
신경망의 선형모델

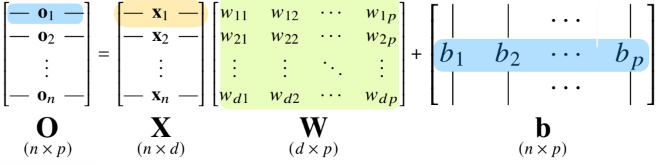
• 선형회귀 문제에서는 주어진 $X$ 에 대해서 다른 공간으로 보내주는 선형변환 $W$와 절편b의 합을 통해 이루어 진다.

• 이때 출력벡터$O$의 차원은 $p$로 바뀌게 된다.
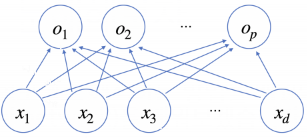
• 이 그림에서 화살표들의 값은 $w$ 로보면 된다.

비선형 모델인 신경망(neural network)

분류 문제에서의 활성화 함수 softmax

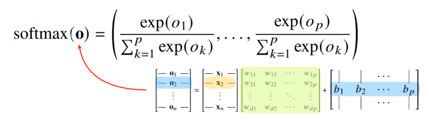
• 소프트맥수(softmax)는 모델의 출력을 확률로 해석할 수 있게 변환해 주는 연산
• 출력벡터$o$에 softmax를 합성하면 확률벡터가 됨
  • 이는 특정클래스 $k$에 속할 확률로 해석할 수 있다

• 이처럼 분류문제를 풀 때 선형모델과 소프트맥스 함수를 결합하여 예측한다.
• 하지만 추론을 할 때는 확률의 max값을 도출하므로 one-hot벡터를 사용
  • 학습 : 모델을 만드는 과정
  • 추론 : 만들어진 모델을 활용하여 Input에 대한 결과를 도출하는 것\
  • 학습을 할 때는 softmax가 필요하지만 추론의 경우 softmax를 쓸 이유가 없다

활성함수

• 신경망은 선형모델과 활성함수를 함성한 함수

• 활성화 함수는 각 z값들의 주소값을 받아 계산되기 때문에 벡터가 아닌 하나의 실수값을 가지고 각각 계산되게 된다.

  • 이를통해 비선형변환이 가능하게 되고, 새로운 잠재벡터 $H$를 얻게 된다.

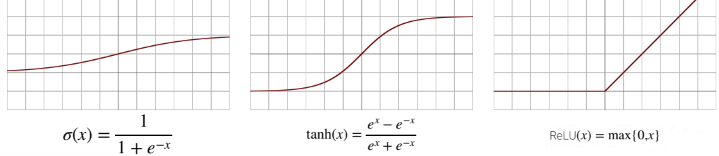
• 활성함수는 실수집합에서 정의된 비선형 함수로 딥러닝에서 매우 중요한 개념

• 활성함수를 쓰지 않으면 딥러닝은 선형모형과 차이가 없게 된다.

• sigmoid함수나 tanh함수는 전통적으로 많이 쓰이던 활성함수지만 딥러닝에선 ReLU 함수를 많이 씀

다층 퍼셉트론

위에서 정의된 신경망(선형모델, 활성함수)를 여러게 쌓게 되면 다층 퍼셉트론

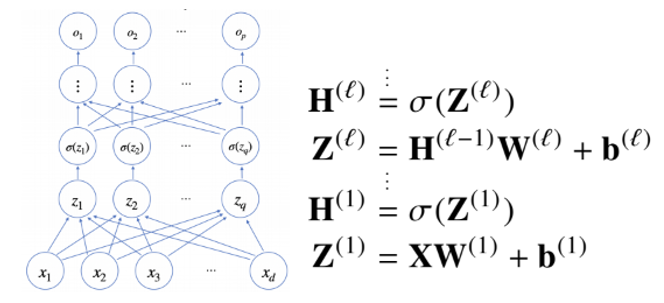
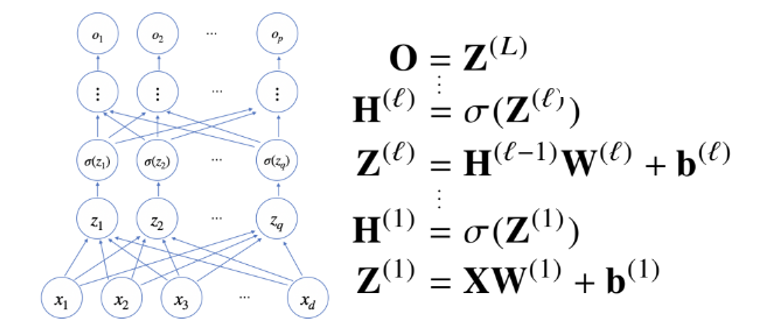
이렇게 $l = 1,...,L$까지 순차적인 신경망 계산을 순전파(forward propagation)이라 부른다

왜 층을 여러개 쌓을까?

• 이론적으로는 2층신경망으로도 임의의 연속함수를 근사할 수 있다.
  (universal approximation theorem)
• 하지만 층이 깊을수록 목적함수를 근사하는데 필요한 뉴런(노드)의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능
  • 최적화를 보장한다는 뜻은 아니다.

역전파

• 딥러닝은 역전파 알고리즘을 통해 각 층에 사용된 파라미터 $W,b$를 학습한다.