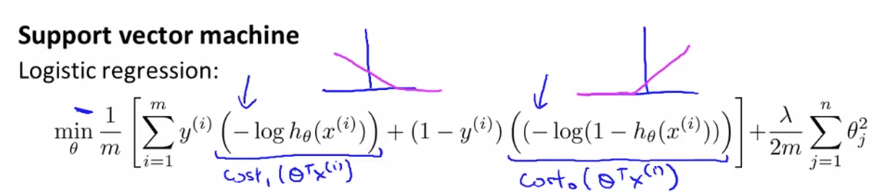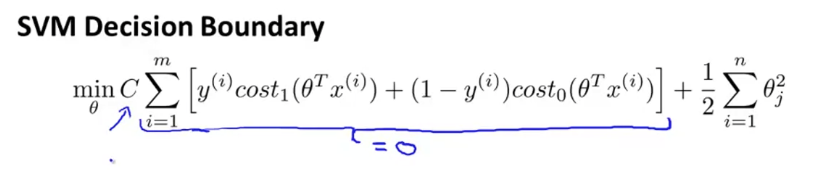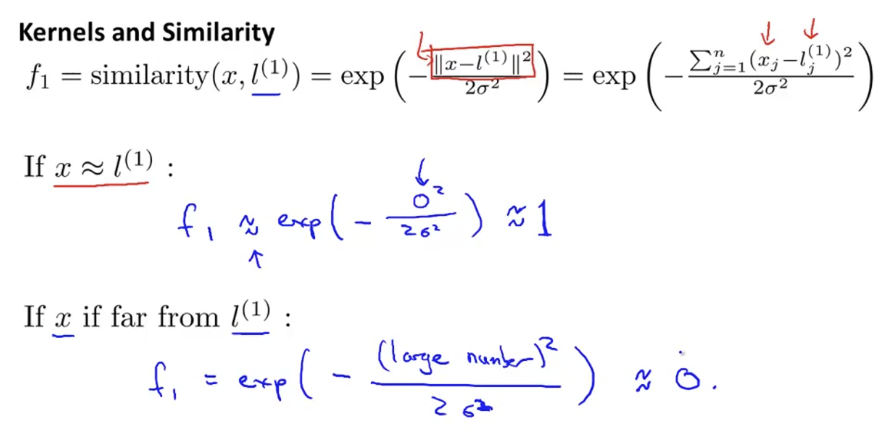[ML] Support Vector Machines

이번에는 Support Vector Machines 알고리즘에 대해 배워보도록 할 것이다. SVMs는 가장 강력한 'black box' learning algorithm으로서 오늘날 가장 널리 쓰이고 있는 알고리즘 중 하나이다. logistic regression과 neural networks와 비교하면, SVM이 learning complex non-linear function에서 더 좋은 해결책이 된다.

Large Margin Classification

Opimization Objective

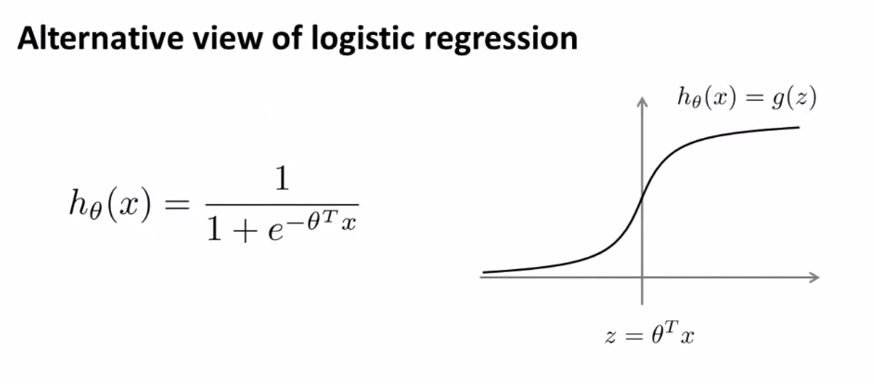
Logistic Regression의 hypothesis function을 다시 살펴보자.

$y=1$이면, 우리는 $h_{\theta}(x)≈1,\;\theta^Tx≫0$이길 원한다.
$y=0$이면, 우리는 $h_{\theta}(x)≈0,\;\theta^Tx≪0$이길 원한다.
따라서 위를 만족하는 $\theta$를 알기 원했다.
(≫, ≪는 much much greater than 이라는 뜻임.)

single training example에서의 Cost는 다음과 같다.

$Cost\;of\;Example = -ylog(h_{\theta}(x^{(i)})+(1-y)log(1-h_{\theta}(x)) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=-ylog(\frac{1}{1+e^{-\theta^Tx}})+(1-y)log(1-\frac{1}{1+e^{-\theta^Tx}})$

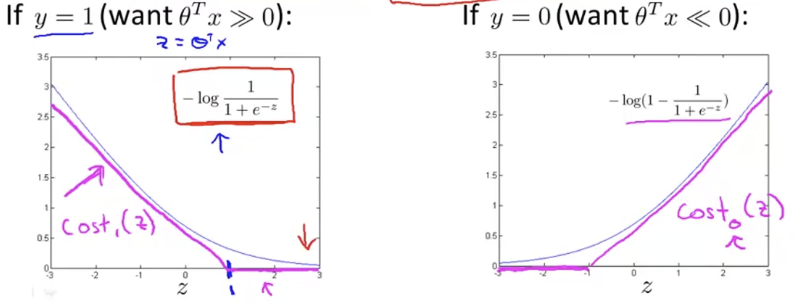
Logistic regression은 log 를 이용해서 cost function을 정의했다. 그러나 SVM은 piecewise-linear function(a function whose domain can be decomposed into pieces on which the function is linear)를 대신 이용한다. 이 함수를 hinge loss function(a loss function used for training classifiers)이라고 부른다.
즉, 위 그래프에서 마젠타색으로 그린 그래프가 cost function이 된다. 이 cost function들의 이름을 각각 $cost_1(z)$, $cost_0(z)$라고 하자.

위에 나타낸 logistic regression 정의들로부터 SVM을 빌드해보자.

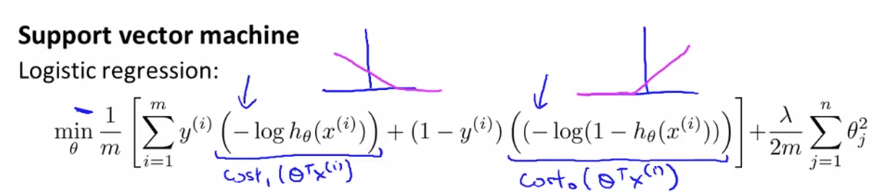
Logistic Regression에서는 $\frac{1}{m}[{\sum\limits_{i=1}^m}y^{(i)}(-log(h_{\theta}(x^{(i)}))+(1-y^{(i)})(-log(1-h_{\theta}(x)))]+\frac{\lambda}{2m}{\sum\limits_{j=1}^n}\theta_j^2$을 최소화하는 $\theta$를 찾길 원했다. 여기서 $-log(h_{\theta}(x^{(i)})$를 $cost_1(\theta^Tx^{(i)})$라고 하고, $-log(1-h_{\theta}(x^{(i)})$를 $cost_0(\theta^Tx^{(i)})$라고 하자.
logistic regression과 비교해서, SVM에선 m항을 제거할 것이다. 왜냐면 m은 상수이기 때문에 $\theta$의 값에 영향을 미치지 않기 때문이다.
또, Logistic Regression에서는 cost function이 $A+\lambda B$꼴이었지만, Support vector machine에서는 $cA+B\;(c=\frac{1}{\lambda})$ 꼴로 cost function을 정의한다. convention이기 때문이다.
그렇게 하면 SVM은 다음과 같다.

Super Vector Machine

$min_\theta\;C{\sum\limits_{i=1}^m}y^{(i)}cost_1(\theta^Tx^{(i)})+(1-y^{(i)})cost_0(\theta^Tx^{(i)})+\frac{1}{2}{\sum\limits_{j=1}^n}\theta_j^2$

• Cost Function
  $J(\theta)=C{\sum\limits_{i=1}^m}y^{(i)}cost_1(\theta^Tx^{(i)})+(1-y^{(i)})cost_0(\theta^Tx^{(i)})+\frac{1}{2}{\sum\limits_{j=1}^n}\theta_j^2$
• SVM hypothesis
  $h_\theta(x)= \begin{cases} 1,\;if\;\theta^Tx≥0\\ 0,\;otherwise \end{cases}$

$J(\theta)=\frac{1}{2m}[{\sum\limits_{i=1}^m}(h_{\theta}(x^{(i)}) - y^{(i)})^2+\lambda{\sum\limits_{j=1}^m}\theta_j^2]$

$J(\theta) = \frac{1}{m}[{\sum\limits_{i=1}^m}y^{(i)}(-log(h_{\theta}(x^{(i)}))+(1-y^{(i)})(-log(1-h_{\theta}(x)))]+\frac{\lambda}{2m}{\sum\limits_{j=1}^n}\theta_j^2$

Large Margin Intuition

때때로 사람들은 SVM을 large margin classifier라고 부른다. 이번에는 이게 무슨 뜻인지와 SVM hypothesis에 대해 좀 더 자세히 살펴보겠다.

아래 그림은 Support Vector Machine 식과, cost 그래프를 나타낸 것이다.

$\theta^Tx$가 0일 때를 기준으로 classification하지 않고, +1, -1일 때를 기준으로 하는 것을 볼 수 있다. 이것은 더 안전한 margin을 갖게 해준다. 이 뜻을 더 잘 이해하기 위해 C가 아주 큰 상황($C=100000$)을 가정해보자.

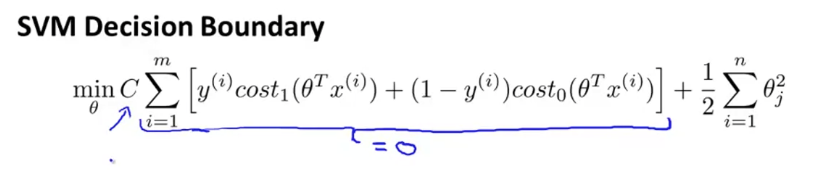
만약 C가 아주 크다면, C를 포함한 항은 거의 0에 가까워야 할 것이다. 이제 이 항을 0에 가깝게 만들어보도록 하자.

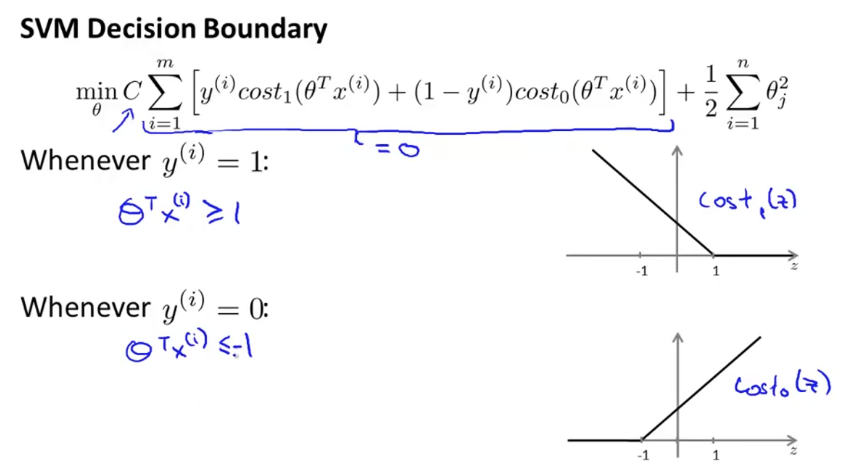
y=1인 경우, $\theta^Tx^{(i)}$는 1보다 같거나 커야하고, y=0인 경우, $\theta^Tx^{(i)}$는 -1보다 같거나 작아야 한다.

${\sum\limits_{i=1}^m}[y^{(i)}(-log(h_{\theta}(x^{(i)}))+(1-y^{(i)})(-log(1-h_{\theta}(x)))]$를 0에 가깝게 만들 것이므로, 위 SVM 식은,

가 되고,

이다.
즉, 다음과 같다.

아래 그림에서 Decision Boundary들을 살펴보자.

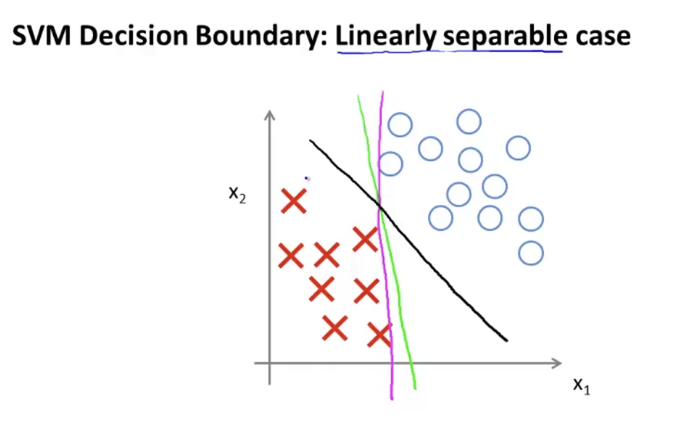
검은색 선으로 그린 Decision Boundary가 마젠타나 초록색으러 그린 바운더리보다 두 클래스를 더 잘 나누고 있는 모습을 보여준다. 더 잘 나누는 것처럼 보이는 이유는, 검은선은 두 class 사이로부터 margin을 최대화하고 있기 때문이다.

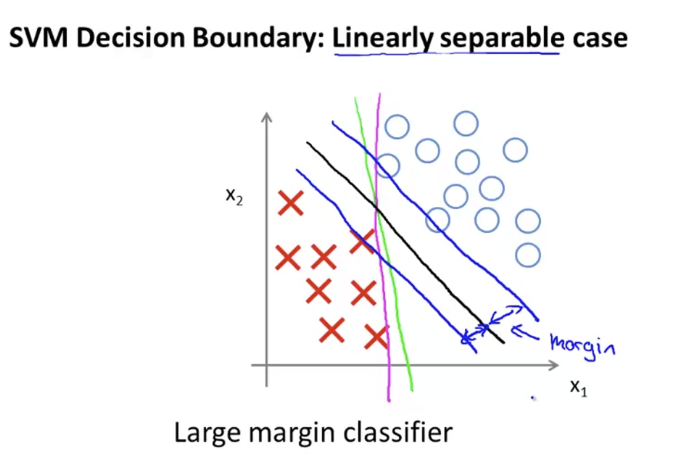
위처럼 검은색 선이 margin을 최대화 하고 있는 모습을 볼 수 있다. 이러한 이유 떄문에 SVM을 Large Margin Classifier로 부른다. 이렇게 되는 이유는 조금 뒤에 살펴본다.

다음과 같은 data set이 있을 때, Decision Boundary를 그린다고 해보자.

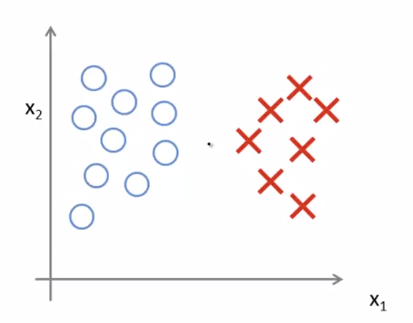
아마 아래와 같은 Decision Boundary를 그리게 될 것이다.

하지만 아래와 같은 데이터가 추가되었다고 해보자.

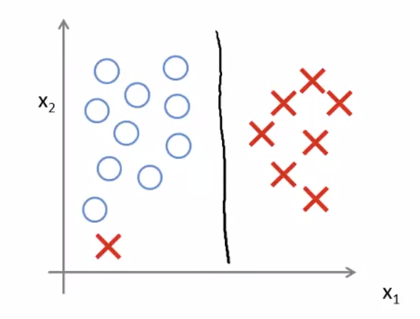
C가 아주 크면, SVM은 Decision Boundary를 다음과 같이 바꾼다.

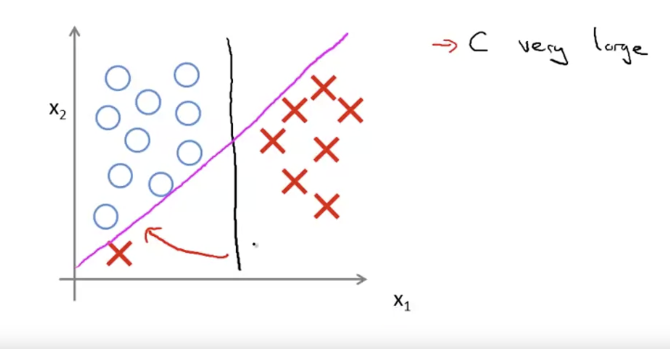
data는 linear하지 않고, $C=\frac{1}{\lambda}$이기 때문에, 이들을 잘 고려해서 C값을 설정해줘야 한다.

Kernels

이제, complex nonlinear classifier을 개발하기 위해 SVM을 적용해볼 것이다. 메인 테크닉은 커널이라고 불리는 기술이다.

Kernels 1

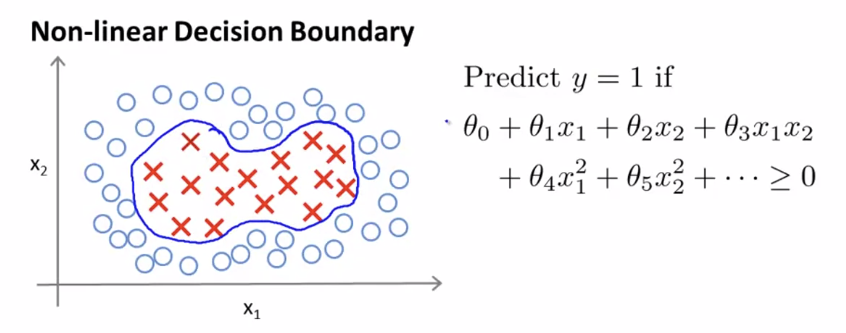
위와 같은 data가 있다고 가정하자. non-linear decision boundary가 필요하다.

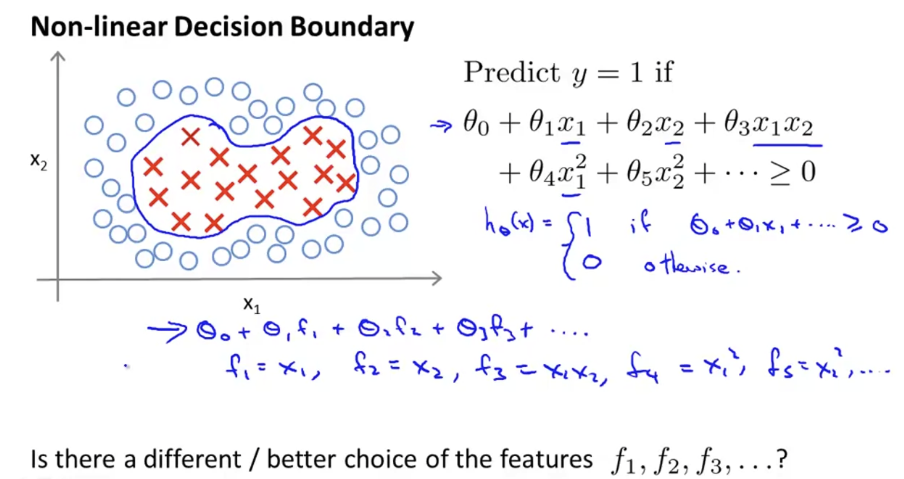
여기서 SVM classifier는 $\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1x_2+...≥0$ 일 때 $y=1$이 되도록 할 것이다. $x_1,x_2,x_1x_2...$와 같은 feature들을 일반적인 형태로 표현하기 위해 $f_1,f_2,...$ 형태로 고쳐써보자. $f_1,f_2,...$를 어떻게 define할 수 있는지 알아보자.

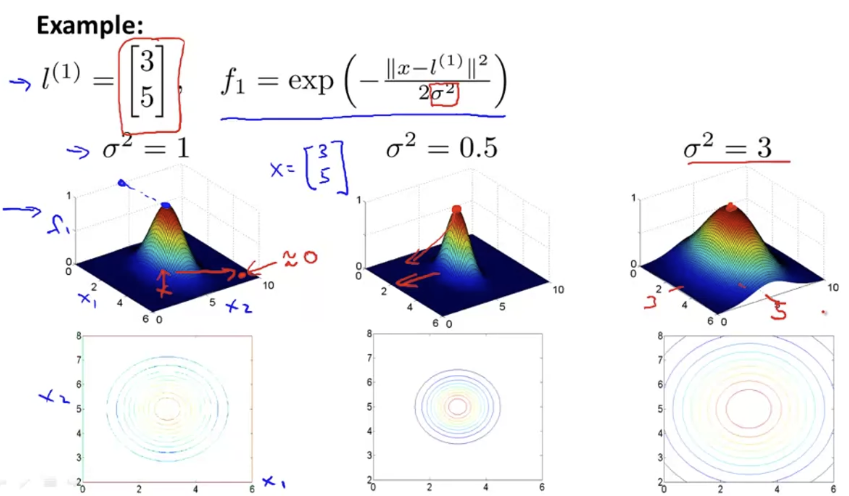
feature space에 임의의 landmark $l^{(1)},l^{(2)},l^{(3)}$이 있다고 가정하자. 주어진 $x$ (즉, $f_1,f_2,...$)에 대하여, landmark $l^{(1)},l^{(2)},l^{(3)}$에 가까운가를 나타내는 새로운 feature $f_i$을 계산하자. 위 $similarity$ 함수를 쓴 식처럼 말이다. ($f_i=similarity(x,l^{(i)})$는 $f_i=k(x,l^{(i)})$로도 나타낼 수 있다.) 여기서는 가우시안 함수를 사용해서 나타냈다. 이 함수는 정규분포곡선 같은 bell-curve 형태이고, landmark에 가까울 수록 큰 값을, 멀 수록 작은 값을 출력한다.

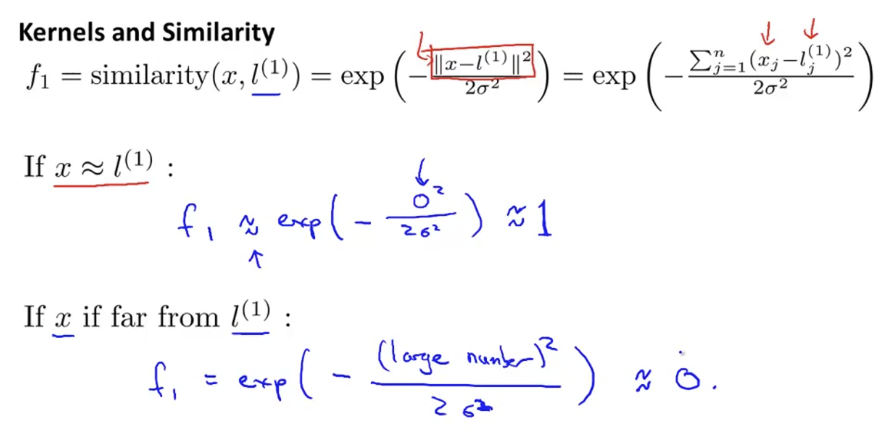
만약 x가 landmark $l^{(1)}$에 가깝다면, $f_1≈exp(-\frac{0^2}{2\sigma^2})≈1$이 된다.
만약 x가 landmark $l^{(1)}$로부터 멀다면, $f_1≈exp(-\frac{large^2}{2\sigma^2})≈0$이 된다.

$\sigma$값에 따라 $f$가 어떻게 변화하는지 살펴보자. 아래 그림은 $\sigma$값에 따라 $f_1$의 그래프를 나타낸 것이다. $\sigma$가 클수록 뭉뚝한 형태를 띄고, 작을 수록 뾰족한 형태를 띈다. 앞에서 말했지만, x가 landmark에 가까울 수록 큰 값을, 멀 수록 작은 값을 출력한다.

---

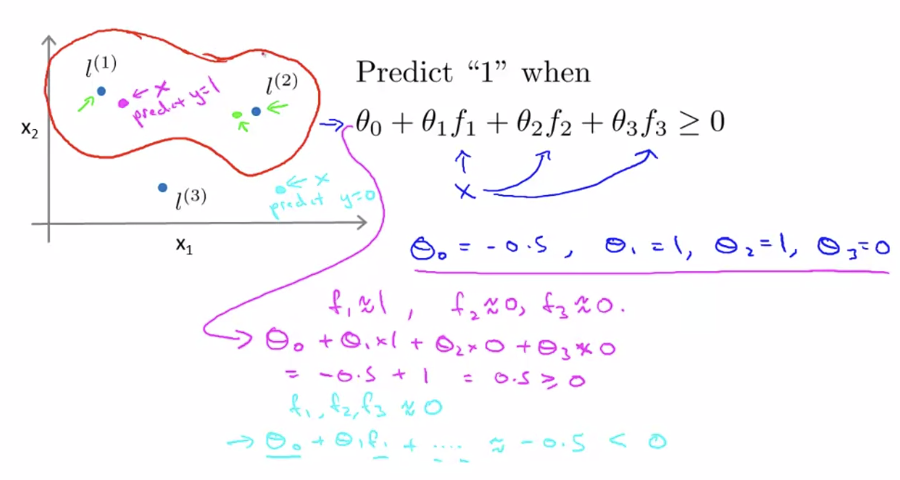
위와 같은 landmark가 있다고 하자. $\theta_0=-0.5,\theta_1=1,\theta_2=1,\theta_3=0$이라고 하자.

위와 같은 경우, $x$는 $f_1$와 가깝고, $f_2,f_3$과는 거리가 있으므로, $f_1≈1,f_2≈0,f_3≈0$이 된다. 따라서, $\theta_0+\theta_1f_1+\theta_2f_2+\theta_3f_3≥0$은 $\theta_0+\theta_1≥0$이 되고, 이것은 0.5≥0이 되므로, 해당하는 점은 y=1영역에 포함된다. 이와 같은 방법으로 여러 위치의 $x$를 입력하여 어떤 $y$값이 출력되는지 계산하면 decision boundary를 구할 수 있다.

Kernels 2

이번엔 어떻게 Landmark를 선택하는지 알아보도록 하자.

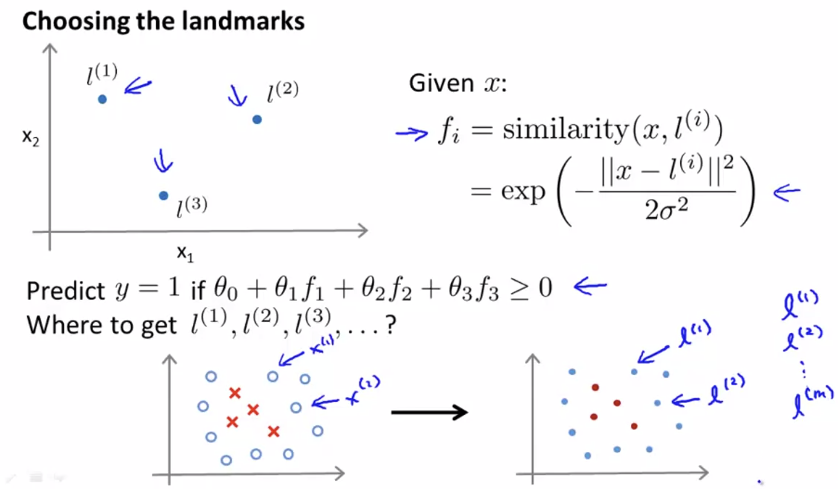
먼저 training example과 같은 위치에 landmark를 둘 수 있다. 위 그림의 오른쪽 그래프에 있는 원의 색깔은 중요치 않다.

---

Kernel을 도입한 SVM은 다음과 같다.

SVM with Kernels

• Hypothesis
  Given $x$, compute features $f∈ℝ^{(m+1)}$
  Predict $y=1$ if $\theta^Tf≥0$
  (단, $\theta^Tf=\theta_0f_0+\theta_1f_1+...+\theta_mf_m$)
• Training
  $min_\theta\;C[{\sum\limits_{i=1}^m}y^{(i)}cost_1(\theta^Tf^{(i)})+(1-y^{(i)})cost_0(\theta^Tf^{(i)})]+\frac{1}{2}{\sum\limits_{j=1}^n}\theta_j^2$

kernel개념을 도입하는 것은 SVM이 아닌 곳에도 가능하지만, SVM 외의 classifier에서는 연산속도가 매우 느려지기 때문에, kernel은 SVM에서만 사용한다.

SVMs in Practice

Using an SVM

SVM은 이미 잘 알려진 알고리즘이고 잘 구현된 library가 많기 때문에 직접 구현해서 사용하기보다는 구축되어 있는 package를 이용하는 게 좋다. (예: liblinear, libsvm, ...) 단, parameter C와 kernel의 종류는 꼭 명시해야 한다.

또, 모든 similarity function $similarity(x,l)$을 kernel로 사용할 수 있는 것은 아니다. "Mercer Theorem"이라는 조건을 만족해야 SVM package의 optimization과정이 발산하지 않고 제대로 동작한다.

많은 SVM 패키지는 이미 multi-class classification을 빌트인으로 가지고 있다. 그 외에는 one vs all method를 사용한다.