학부시절 자료구조,알고리즘 수업이 정말 재미없어서 대충 공부한것을 후회하면서,,
다시 한번 공부해보자!!!👩💻
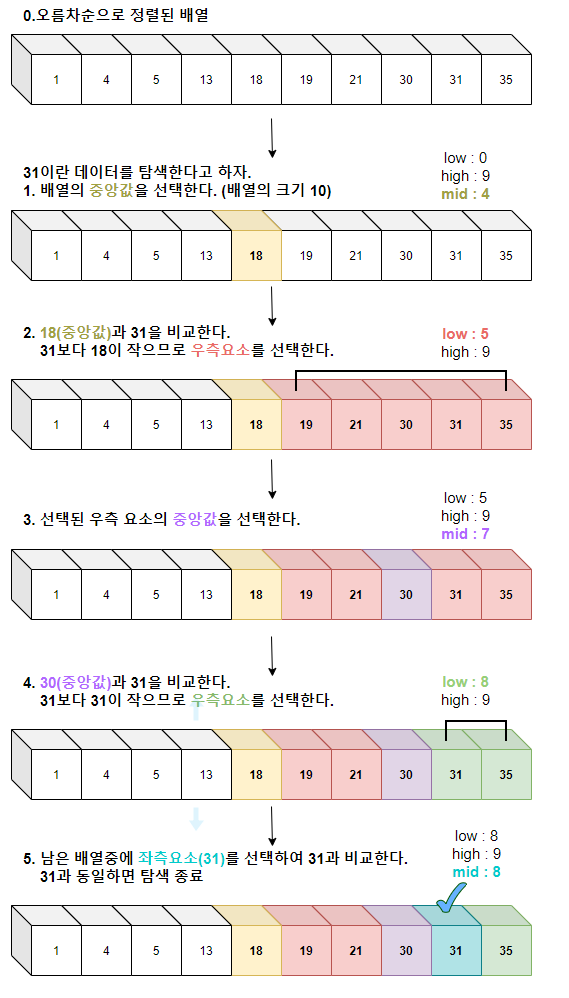
이분탐색(이진탐색)이란?
오름차순으로 정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘이다.
처음과 마지막의 중간값을 선택하여,
찾고자 하는 값과 크고 작음을 비교하는 방식으로 반복하여 탐색을 진행한다.
필수조건 : 오름차순으로 정렬된 리스트
장점 : 모든 값을 순회하는 일반탐색보다는 속도가 빠르다.
시간 복잡도 : log2N ( 한 번 탐색할때마다 , 탐색의 범위가 1/2로 줄어 들기 때문에)
🎨그림으로 이해해보자!
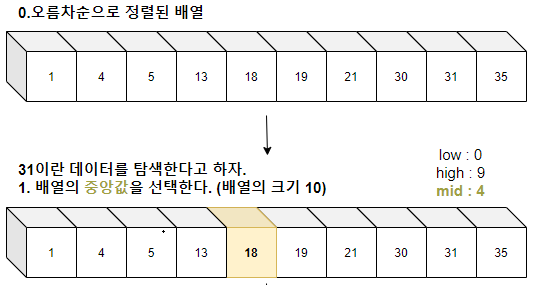
0. 주어진 배열을 오름차순으로 정렬
1. low : 최소값의 인덱스 / high : 최고값 인덱스 / mid : 중간값 인덱스로 각각 초기 설정
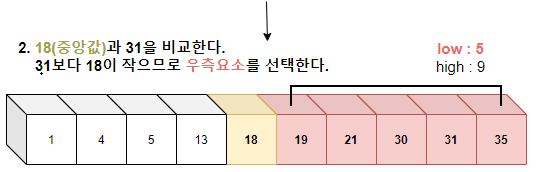
2.설정된 중앙값(mid)가 31보다 작으므로, low 의 인덱스를 mid+1로 설정하여 우측을 선택한다.
(반대로, 중앙값이 31보다 큰 경우라면, high 인덱스를 mid-1로 설정하여 좌측을 선택한다.)
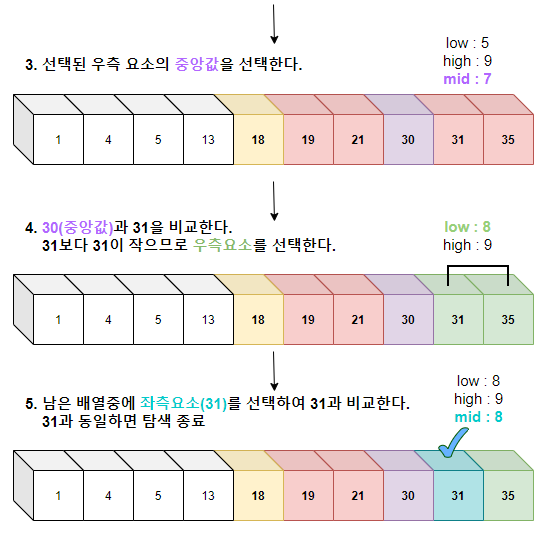
3~5. 위의 1~2번 탐색과정을 답을 찾을때까지 반복과정 (단, low과 high보다 커지는 경우 탐색은 종료된다.)
이분탐색 코드로 이해하기
위의 예제를 이용하여 코드로 작성해보자.
public static void main(String[] args) {
int[] arr = new int[] {31,18,5,4,19,35,1,13,30,21};
binarySearch_loop(arr, 31);
binarySearch_recursive(arr, 0, arr.length-1, 31);
}
// 반복문을 이용
public static int binarySearch_loop(int[] arr, int target) {
Arrays.sort(arr); // 0번 과정 : 오름차순 정렬
int low = 0;
int high = arr.length-1;
int mid = 0;
// 제일 작은수가 큰수보다 커지면 탐색 종료
while(low <= high) {
mid = (low + high) /2; // 1번 과정 : 중앙값 찾기
if(arr[mid] == target) {
return mid;
}else if(arr[mid] > target) { // 현재의 중앙값보다 작으면,
high = mid-1; // 왼쪽요소를 선택하기 위해 high = mid -1로 설정
}else {
low = mid+1; // 현재의 중앙값보다 크면, 오른쪽 요소를 선택하기 위해 low = mid+1로 설정
}
}
// 탐색해도 결과가 없는 경우
return -1;
}
// 재귀함수를 이용
public static int binarySearch_recursive(int[] arr, int low, int high, int target) {
Arrays.sort(arr); // 0번 과정 : 오름차순 정렬
if(low > high) {
return -1;
}
int mid = (low + high) /2; // 1번 과정 : 중앙값 찾기
if(arr[mid] == target) {
return mid;
}else if(arr[mid] > target) {
return binarySearch_recursive(arr, low, mid-1, target);
}else {
return binarySearch_recursive(arr, mid+1, high, target);
}
}[참조블로그]
위키백과 - 이진 검색 알고리즘
탐색 알고리즘 - 이진탐색
이진 탐색(Binary Search) 알고리즘 개념 이해 및 추가 예제