📌 자료의 종류
📖 자료의 특성에 따른 분류
- 범주형자료
질적자료 - 연속형자료
양적자료
✔ 범주형 자료
- 질적자료라고도 부르며, 성별과 같이 범주 또는 그룹으로 구분할 수 있는 값으로 구성된 자료
- 범주형 자료의 값들은 기본적으로 숫자로 표현할 수 없고, 대소 비교나 산술 연산이 적용되지 않음
- 범주형 자료를 숫자로 표기했다고 해서 계산 가능한 연속형 자료가 되는 것은 아님
ex) 성별 : 0,1
ex) 혈액형 : 1,2,3,4
✔ 연속형 자료
- 양적자료라고도 부르며, 크기가 있는 숫자들로 구성된 자료
- 연속형 자료의 값들은 대소 비교가 가능하고, 평균, 최댓값, 최솟값과 같은 산술 연산이 가능
📖 변수 개수에 따른 분류
- 단일변수 자료 : 하나의 변수로만 구성된 자료, '일변량 자료'라고도 부름
- 다중변수 자료 : 두 개 이상의 변수로 구성된 자료, 다변량 자료라고도 부름, 두 개의 변수로 구성된 자료를 이변량 자료
- 단일변수 자료는 벡터에, 다중변수 자료는 매트릭스나 데이터 프레임에 저장하여 분석
- 매트릭스 또는 데이터 프레임 형태의 자료에서 하나의 열이 하나의 변수를 표현
- 열이 개수 = 변수의 개수
- 변수의 개수와 자료의 특성에 따라 세분화된 분류가 가능
<변수의 개수와 자료의 특성에 따라 분류>
-
단일변수자료
범주형 자료
연속형 자료 -
다중변수 자료
범주형 자료
연속형 자료
📌 단일변수 범주형 자료의 탐색
- 단일범수 범주형 자료(일변량 질적 자료) : 특성이 하나이면서 자료의 특성이 범주형인 자료
-범주형 자료에 대해서 할 수 있는 기본적인 작업은 자료에 포함된 관측값들의 종류별로 개수를 세는 것- 개수를 세면 종류별 비율을 알 수 있음
- 막대그래프나 원그래프 작성 가능
- ex) 학생들이 선호하는 계절
📖 도수분포표
> favorite <- c('winter', 'summer','spring','summer','summer',
+ 'fall','fall','summer','spring','spring')
> favorite
[1] "winter" "summer" "spring" "summer" "summer" "fall" "fall"
[8] "summer" "spring" "spring"
> table(favorite) #도수분포표 계산
favorite
fall spring summer winter
2 3 4 1
> table(favorite)/length(favorite) #비율 출력
favorite
fall spring summer winter
0.2 0.3 0.4 0.1 📖 막대그래프
> ds <- table(favorite)
> ds
favorite
fall spring summer winter
2 3 4 1
> barplot(ds, main='favorite season')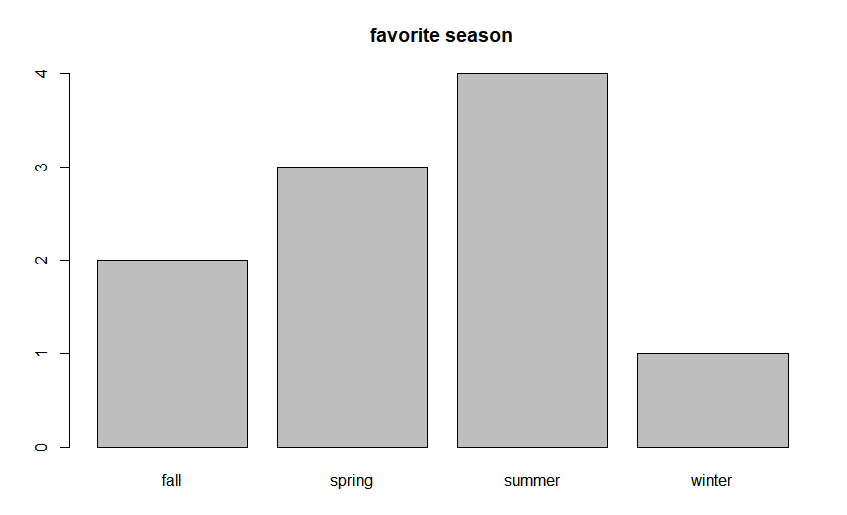
📖 원그래프
> ds <- table(favorite)
> ds
favorite
fall spring summer winter
2 3 4 1
> pie(ds, main='favorite season')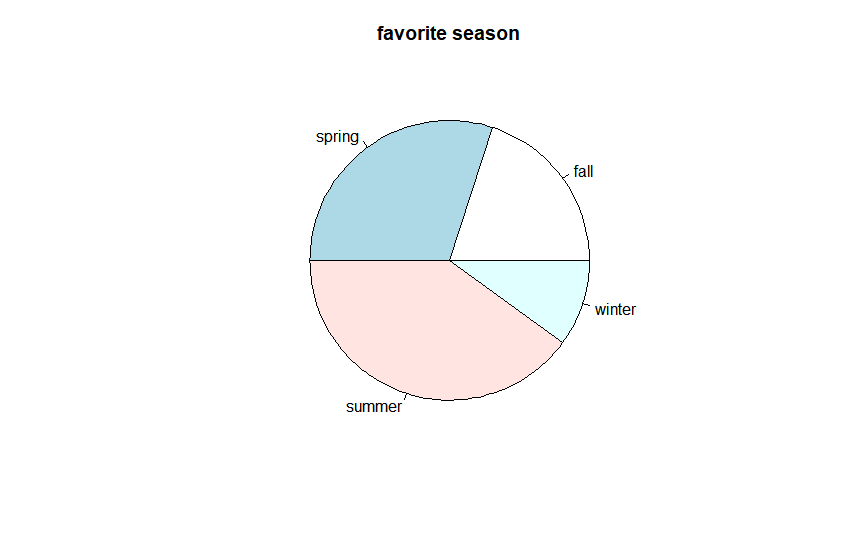
📖 숫자로 표현된 범주형 자료
- 숫자 형태의 범주형 자료도 도수분포를 계산한 후 막대그래프와 원그래프를 그려서 자료의 내용을 확인
ex) 학생 15명이 선호하는 색깔을 조사한 자료
2,3,2,1,1,2,2,1,3,2,1,3,2,1,2
(1=초록, 2=빨강, 3=파랑)
> favorite.color <- c(2,3,2,1,1,2,2,1,3,2,1,3,2,1,2)
> ds <- table(favorite.color)
> ds
favorite.color
1 2 3
5 7 3
> barplot(ds,main='favorite color')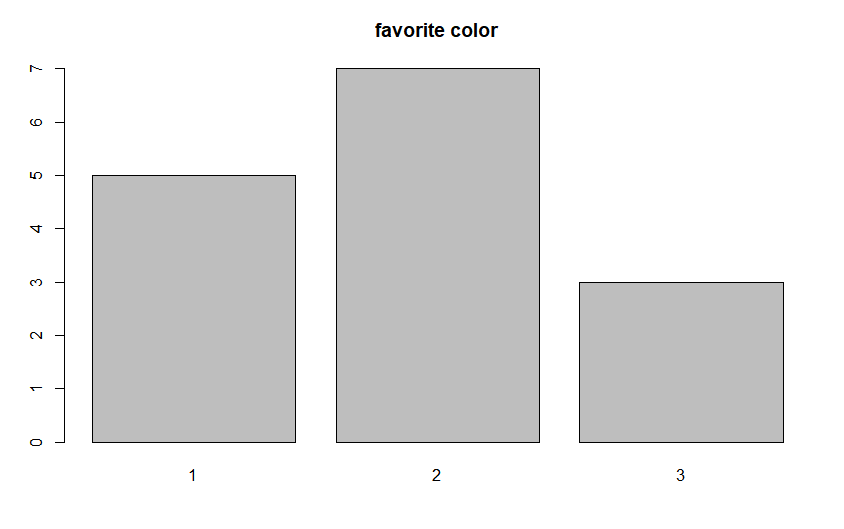
> colors <- c('green','red','blue')
> names(ds) <- colors #자료값 1,2,3을 green, red, blue로 변경
> ds
green red blue
5 7 3
> barplot(ds,main='favorite color', col=colors) #색 지정 막대그래프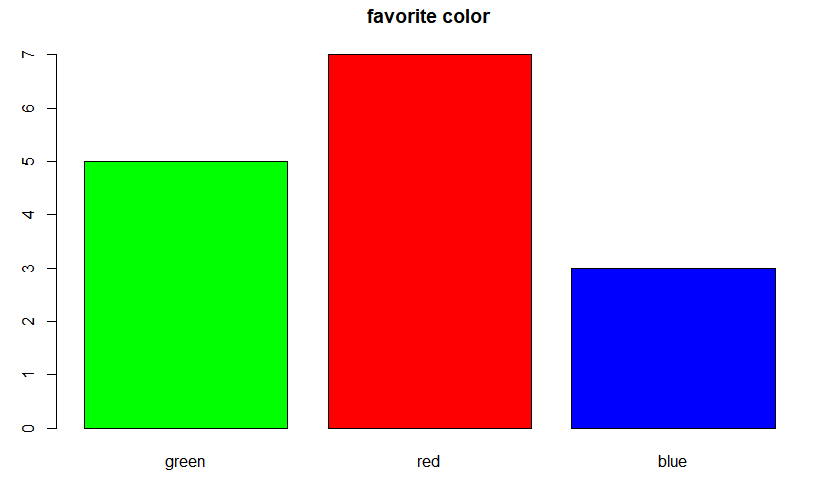
> pie(ds, main='favorite color', col=colors)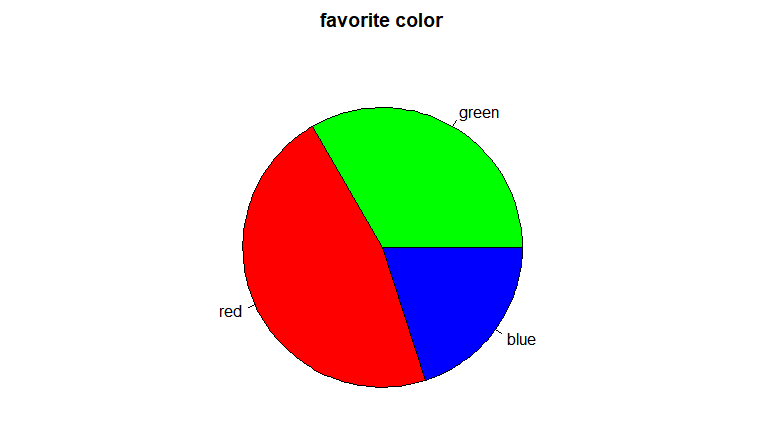
📌 단일변수 연속형 자료의 탐색
📖 평균과 중앙값
- 연속형 자료는 관측값들이 크기를 가지기 때문에 범주형 자료에 비해 다양한 분석 방법 존재
- 평균, 중앙값 : 전체 데이터를 대표할 수 있는 값
- 평균
- 중앙값 : 자료 값들을 크기순으로 일렬로 줄 세웠을 때, 가장 중앙에 위치하는 값
- 절사평균은 자료의 관측값들 중에서 작은 값들의 하위 n%와 큰 값들의 상위 n%를 제외하고 중간에 있는 나머지 값들만 가지고 평균을 계산
> weight <- c(60,62,64,65,68,69)
> weight.heavy <- c(weight,120)
> weight
[1] 60 62 64 65 68 69
> weight.heavy
[1] 60 62 64 65 68 69 120
> mean(weight) #평균
[1] 64.66667
> mean(weight.heavy) #평균
[1] 72.57143
> median(weight) #중앙값
[1] 64.5
> median(weight.heavy) #중앙값
[1] 65
> mean(weight, trim=0.2) #절사평균(상하위 20% 제외)
[1] 64.75
> mean(weight.heavy,trim=0.2) #절사평균(상하위 20% 제외)
[1] 65.6📖 사분위수
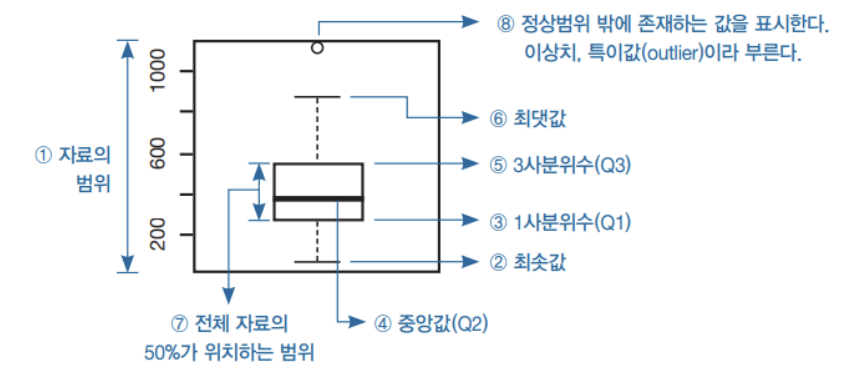
- 사분위수란 주어진 자료의 값들을 크기순으로 나열했을 때 이것을 4등분하는 지점에 있는 값들을 의미
- 자료에 있는 값들을 4등분하면 등분점 3개 생기는데, 앞에서부터 '제1사분위수(Q1)', '제2사분위수(Q2)', '제3사분위수(Q3)'라고 부르며, 제2사분위수(Q2)는 중앙값과 동일
- 전체 자료를 4개로 나누었기 때문에 4개의 구간에는 각각 25%의 자료가 존재

ex) 100명의 학생을 대상으로 영어시험을 본 결과에 대해 사분위수를 구하였더니
Q1=60, Q2=80, Q3=90이라고 가정하면 →
25명의 학생은 성적이 60점 미만이다.
25명의 학생은 성적이 60점~80점 사이이다.
25명의 학생은 성적이 80점~90점 사이이다.
25명의 학생은 성적이 90점 이상이다.
90점 이상인 학생이 25명이나 되기 때문에 이번 영어시험은 매우 쉬웠다.
전체 50%의 학생이 80점 이상의 성적을 받았다.
> mydata <- c(60,62,64,65,68,69,120)
> quantile(mydata)
0% 25% 50% 75% 100%
60.0 63.0 65.0 68.5 120.0
> quantile(mydata, (0:10)/10) #10% 단위로 구간을 나누어 계산
0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
60.0 61.2 62.4 63.6 64.4 65.0 66.8 68.2 68.8 89.4 120.0
> summary(mydata)
Min. 1st Qu. Median Mean 3rd Qu. Max.
60.00 63.00 65.00 72.57 68.50 120.00📖 산포
- 산포란 주어진 자료에 있는 값들이 퍼져 있는 정도(흩어져 있는 정도)
- 산포는 분산과 표준편차를 가지고 파악
- 자료의 분산과 표준편차가 작다는 의미는 자료의 관측값들이 평균값 부근에 모여 있다는 뜻
> mydata <- c(60,62,64,65,68,69,120)
> var(mydata) #분산
[1] 447.2857
> sd(mydata) #표준편차
[1] 21.14913
> range(mydata) #값의 범위
[1] 60 120
> diff(range(mydata)) #최댓값, 최솟값의 차이
[1] 60📖 히스토그램
- 히스토그램은 외관상 막대그래프와 비슷한 그래프로, 연속형 자료의 분포를 시각화할 때 사용
- 막대그래프를 그리려면 값의 종류별로 개수를 셀 수 있어야 하는데, 키와 몸무게 등의 자료는 값의 종류라는 개념이 없어서 종류별로 개수를 셀 수 없음
- 연속형 자료에서는 구간을 나누고 구간에 속하는 값들의 개수를 세는 방법을 사용
> dist <- cars[,2] #자동차 제동거리
> hist(dist, #자료
+ main="Histogram for 제동거리", #제목
+ xlab="제동거리", #x축 레이블
+ ylab="빈도수", #y축 레이블
+ border="blue", #막대 테두리색
+ col="green", #막대색
+ las=2, #x축 글씨 방향(0~3)
+ breaks=5) #막대 개수 조절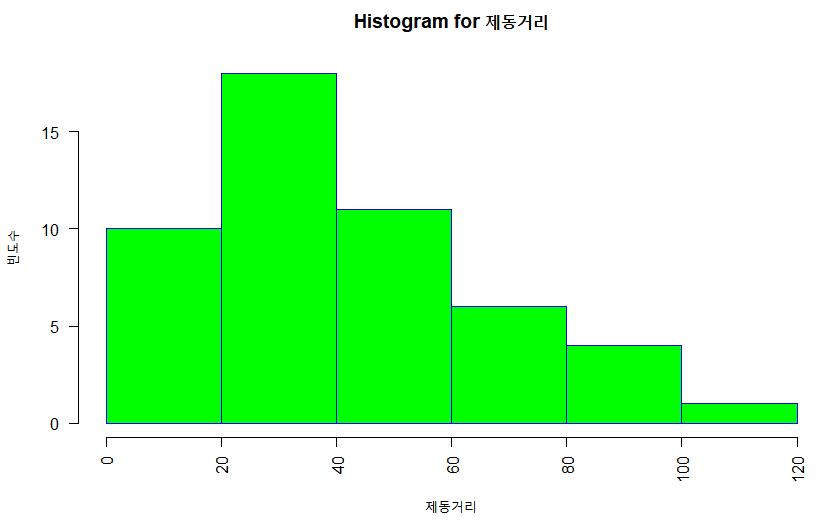
* 막대그래프와 히스토그램 비교
- 막대 사이에 간격이 있으면 막대그래프
- 간격 없이 막대들이 붙어 있으면 히스토그램
- 막대그래프는 막대의 면적이 의미가 없지만, 히스토그램은 막대의 면적도 의미가 있음
📖 상자그림
- 상자그림은 상자 수염 그림으로도 부르며, 사분위수를 시각화하여 그래프 형태로 나타낸 것
- 하나의 그래프로 데이터의 분포 형태를 포함한 다양한 정보를 전달하기 때문에 단일변수 수치형 자료를 파악하는데 자주 사용
> dist <- cars[,2] #자동차 제동거리
> boxplot(dist, main="자동차 제동거리")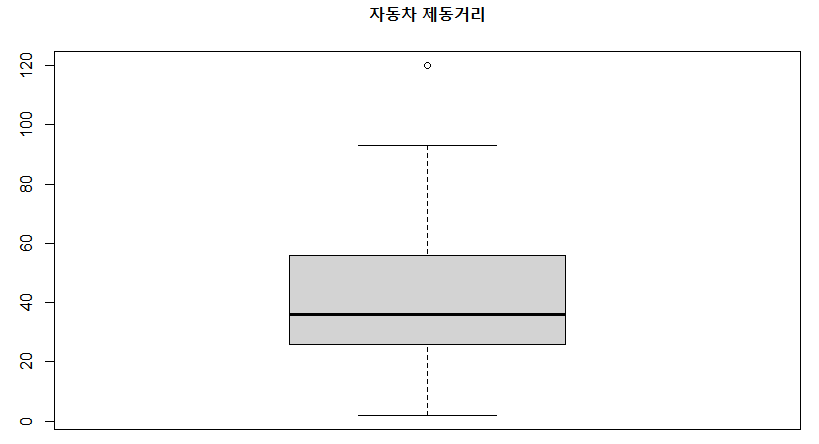
> boxplot.stats(dist)
$stats
[1] 2 26 36 56 93
$n
[1] 50
$conf
[1] 29.29663 42.70337
$out
[1] 120📖 그룹이 있는 자료의 상자그림
> boxplot(Petal.Length~Species, data=iris, main="품종별 꽃잎의 길이")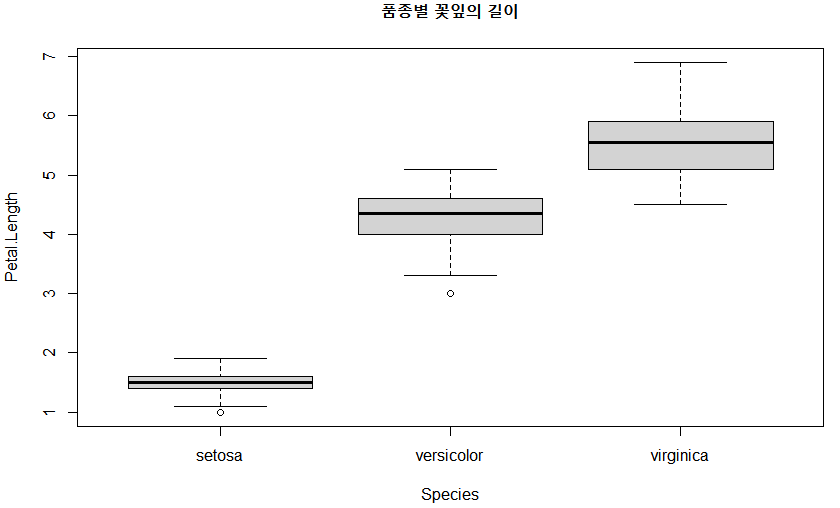
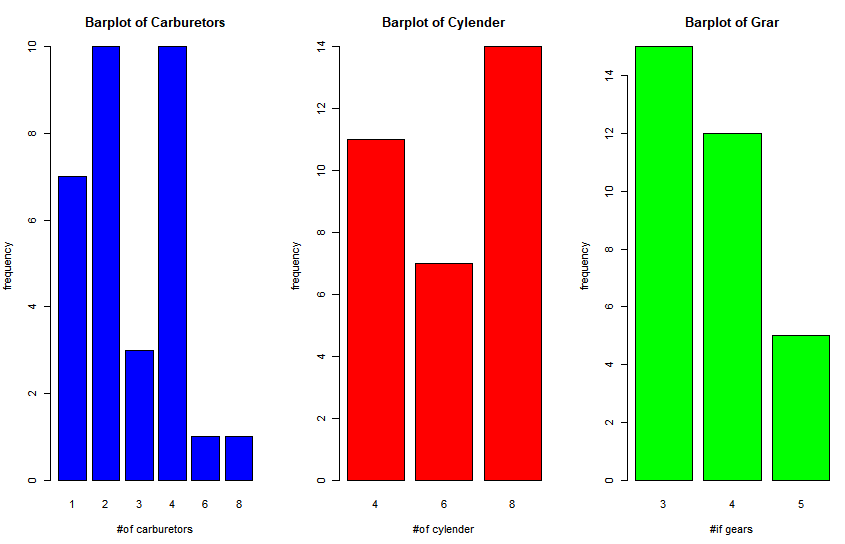
📖 한 화면에 그래프 여러 개 출력하기
> par(mfrow=c(1,3)) #1X3 가상화면 분할
> barplot(table(mtcars$carb),
+ main="Barplot of Carburetors",
+ xlab="#of carburetors",
+ ylab="frequency",
+ col="blue")
> barplot(table(mtcars$cyl),
+ main="Barplot of Cylender",
+ xlab="#of cylender",
+ ylab="frequency",
+ col="red")
> barplot(table(mtcars$gear),
+ main="Barplot of Grar",
+ xlab="#if gears",
+ ylab="frequency",
+ col="green")
par(mfrow=c(1,1)) #가상화면 분할 해제