📌 산점도
- 다중변수(또는 다변량 자료) : 변수가 2개 이상인 자료
- 다중변수 자료는 2차원 형태를 나타내며, 매트릭스나 데이터 프레임에 저장하여 분석
- 산점도란 2개의 변수로 구성된 자료의 분포를 알아보는 그래프
✔ 두 변수 사이의 산점도
mtcars 데이터셋에서 자동차의 중량(wt)과 연비(mpg) 사이의 관계
> wt <- mtcars$wt #중량 자료
> mpg <- mtcars$mpg #연비 자료
> plot(wt, mpg, #2개의 변수(x축, y축)
+ main="중량-연비 그래프", #제목
+ xlab="중량", #x축 레이블
+ ylab="연비(MPG)", #y축 레이블
+ col="red", #point의 color
+ pch=19) #point의 종류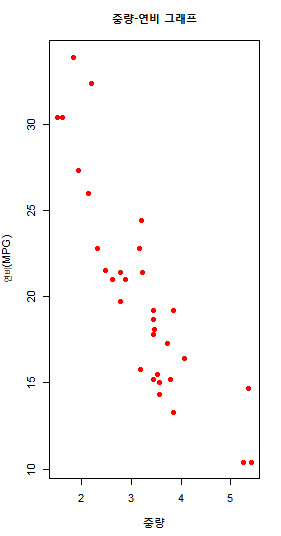
중량이 증가할수록 연비는 감소하는 경향을 확인
✔ 여러 변수들 간의 산점도
> vars <- c("mpg","disp","drat","wt") #대상 변수
> target <- mtcars[,vars]
> head(target)
mpg disp drat wt
Mazda RX4 21.0 160 3.90 2.620
Mazda RX4 Wag 21.0 160 3.90 2.875
Datsun 710 22.8 108 3.85 2.320
Hornet 4 Drive 21.4 258 3.08 3.215
Hornet Sportabout 18.7 360 3.15 3.440
Valiant 18.1 225 2.76 3.460
> pairs(target, main="Multi Plots") #대상 데이터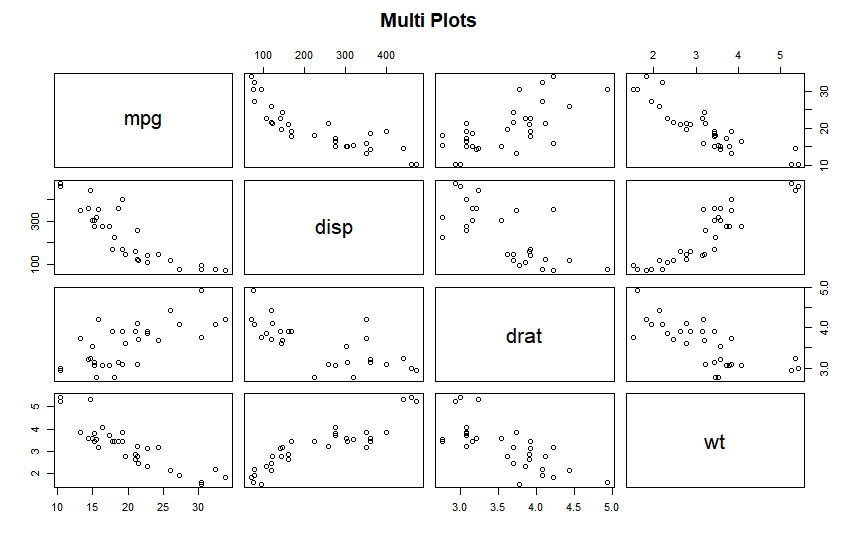
✔ 그룹 정보가 있는 두 변수의 산점도
- 그룹 정보를 알고 있다면 산점도 작성 시 각 그룹별 관측밧들을 다른 색깔과 점의 모양으로 표시할 수 있음
- 이렇게 작성된 산점도는 두 변수 간의 관계뿐만 아니라 그룹 간의 관계도 파악할 수 있어서 편리
> iris.2 <- iris[,3:4] #데이터 준비
> point <- as.numeric(iris$Species) #점의 모양
> point
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[35] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[69] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3
[103] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
[137] 3 3 3 3 3 3 3 3 3 3 3 3 3 3
color <- c("red","green","blue") #점의 컬러
> plot(iris.2,
+ main="iris plot",
+ pch=c(point),
+ col=color[point])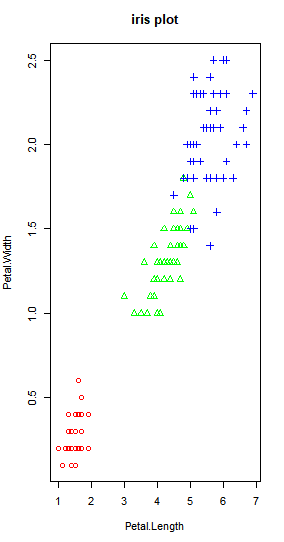
- Petal.Length(꽃잎의 길이)의 길이가 길수록 Petal.Width(꽃잎의 폭)도 커짐
- setosa 품종은 다른 두 품종에 비해 꽃잎의 길이와 폭이 확연히 작음
- virginica 품종은 다른 두 품종에 비해 꽃잎의 길이와 폭이 제일 큼
📌 상관분석
✔ 상관분석과 상관계수
- 자동차의 중량이 커지면 연비는 감소하는 추세
- 추세의 모양이 선 모양이어서 중량과 연비는 '선형적 관계'에 있다고 표현
- 선형적 관계라고 해도 강한 선형적 관계가 있고 약한 선형적 관계도 있음
- 상관분석 : 얼마나 선형성을 보이는지 수치상으로 나타낼 수 있는 방법
- 피어슨 상관계수
- -1<=r<=1
- r>0 : 양의 상관관계 (x가 증가하면 y도 증가)
- r<0 : 음의 상관관계 (x가 증가하면 y는 감소)
- r이 1이나 -1에 가까울수록 x,y의 상관성이 높음
✔ R을 이용한 상관계수의 계산
음주 정도와 혈중알콜농도가 상관성 조사
> beers <- c(5,2,9,8,3,7,3,5,3,5)
> bal <- c(0.1,0.03,0.19,0.12,0.04,0.0095,0.07,0.06,0.02,0.05)
> tbl <- data.frame(beers,bal) #데이터프레임 생성
> tbl
beers bal
1 5 0.1000
2 2 0.0300
3 9 0.1900
4 8 0.1200
5 3 0.0400
6 7 0.0095
7 3 0.0700
8 5 0.0600
9 3 0.0200
10 5 0.0500
> plot(bal~beers, data=tbl) #산점도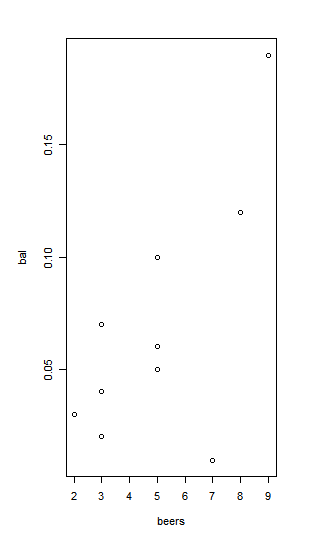
> res <- lm(bal~beers, data=tbl) #회귀식 도출
> abline(res) #회귀선 그리기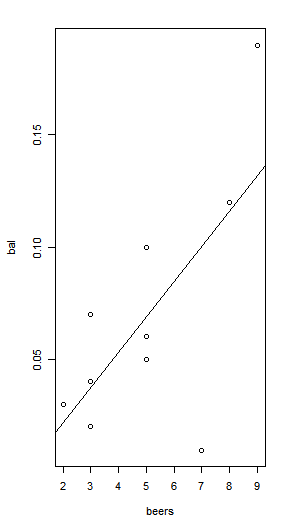
> cor(beers,bal) #상관계수 계산
[1] 0.6797025
> cor(iris[,1:4]) #4개 변수 간 상관성 분석
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411
Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259
Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654
Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000📌 선그래프
✔ 선그래프의 작성
> month <- c(1:12)
> late <- c(5,8,7,9,4,6,12,13,8,6,6,4)
> plot(month, #x data
+ late, #y data
+ main="지각생 통계", #제목
+ type="l", #그래프의 종류 선택
+ lty=1, #선의 종류 선택
+ lwd=1, #선의 굵기 선택
+ xlab="Month", #x축 레이블
+ ylab="Late cnt") #y축 레이블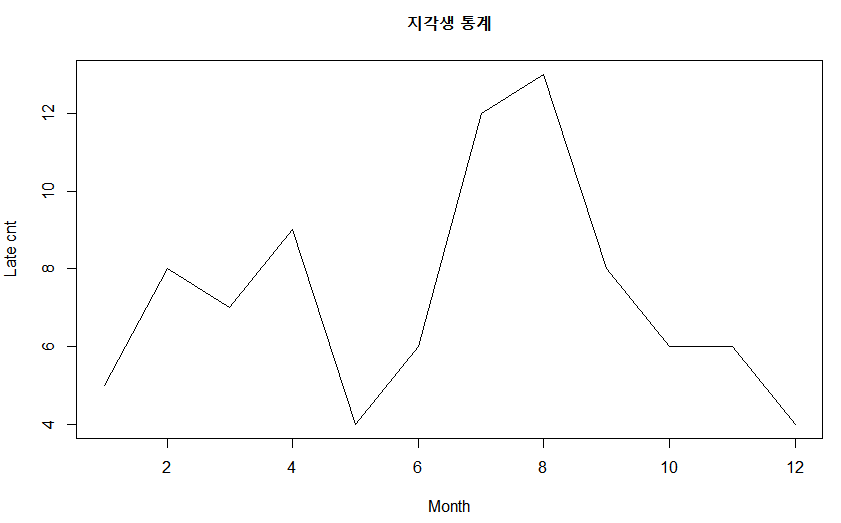
- 다중변수 자료의 변수 중 하나가 연월일과 같이 시간을 나타내는 값을 갖는 경우 x축을 시간 축으로 하여 선그래프를 그리면 시간의 변화에 따른 자료의 증감 추이를 쉽게 확인할 수 잇음
- 시간의 변화에 따라 자료를 수집한 경우, 이를 시계열 자료라고 함
- 선그래프는 시계열 자료의 내용을 파악하는 가장 기본적인 방법
✔ 복수의 선그래프의 작성
> month <- c(1:12)
> late1 <- c(5,8,7,9,4,6,12,13,8,6,6,4)
> late2 <- c(4,6,5,8,7,8,10,11,6,5,7,3)
> plot(month, #x data
+ late1, #y data
+ main="Late Students",
+ type="b", #그래프의 종류 선택
+ lty=1, #선의 종류 선택
+ col="red", #선의 색 선택
+ xlab="Month", #x축 레이블
+ ylab="Late cnt", #y축 레이블
+ ylim=c(1,15)) #y축 값의 (하한, 상한)
> lines(month, #x data
+ late2, #y data
+ type="b", #선의 종류 선택
+ col="blue") #선의 색 선택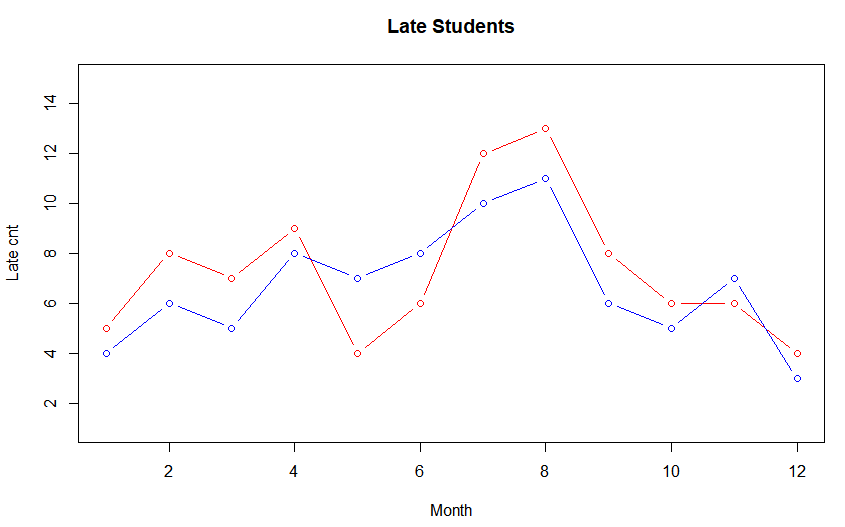
📌 자료의 탐색 실습
✔ Boston Housing 데이터셋
- 미국 보스턴 지역의 주택 가격 정보와 주택 가격에 미치는 여러 요소들에 대한 정보를 담고 있음
- 총 14개의 변수로 구성되어 있는데, 이중에 5개의 변수만 선택하여 분석
- mlbench 패키지에서 제공
crim 지역의 1인당 범죄율
rm 주택 1가구당 방의 개수
dis 보스턴의 5개 직업 센터까지의 거리
tax 재산세율
medv 주택 가격
✔ 탐색적 데이터 분석 과정
분석 대상 데이터셋 준비
> library(mlbench)
경고메시지(들):
패키지 ‘mlbench’는 R 버전 4.0.5에서 작성되었습니다
> data("BostonHousing")
> myds <- BostonHousing[,c("crim","rm","dis","tax","medv")]grap 변수 추가
- grp는 주택 가격을 상(H), 중(M), 하(L)로 분류한 것으로, 25.0이상이면 상(H), 17.0이하이면 하(L), 나머지를 중(M)으로 분류
> grp <- c()
> for(i in 1:nrow(myds)){ #myds$medv 값에 따라 그룹 분류
+ if(myds$medv[i]>=25.0){
+ grp[i] <- "H"
+ } else if (myds$medv[i]<=17.0){
+ grp[i] <- "L"
+ } else {
+ grp[i] <- "M"
+ }
+ }
> grp <- factor(grp) #문자 벡터를 팩터 타입으로 변경
> grp <- factor(grp, levels=c("H","M","L")) #레벨의 순서를 H,L,M -> H,M,L
> myds <- data.frame(myds, grp) #myds에 grp열 추가데이터셋의 형태와 기본적인 내용 파악
> str(myds)
'data.frame': 506 obs. of 6 variables:
$ crim: num 0.00632 0.02731 0.02729 0.03237 0.06905 ...
$ rm : num 6.58 6.42 7.18 7 7.15 ...
$ dis : num 4.09 4.97 4.97 6.06 6.06 ...
$ tax : num 296 242 242 222 222 222 311 311 311 311 ...
$ medv: num 24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 ...
$ grp : Factor w/ 3 levels "H","M","L": 2 2 1 1 1 1 2 1 3 2 ...
> head(myds)
crim rm dis tax medv grp
1 0.00632 6.575 4.0900 296 24.0 M
2 0.02731 6.421 4.9671 242 21.6 M
3 0.02729 7.185 4.9671 242 34.7 H
4 0.03237 6.998 6.0622 222 33.4 H
5 0.06905 7.147 6.0622 222 36.2 H
6 0.02985 6.430 6.0622 222 28.7 H
> table(myds$grp) #주택 가격 그룹별 분포
H M L
132 247 127 히스토그램에 의한 관측값의 분포 확인
> par(mfrow=c(2,3)) #2X3 가상화면 분할
> for(i in 1:5){
+ hist(myds[,i], main=colnames(myds)[i],col="yellow")
+ }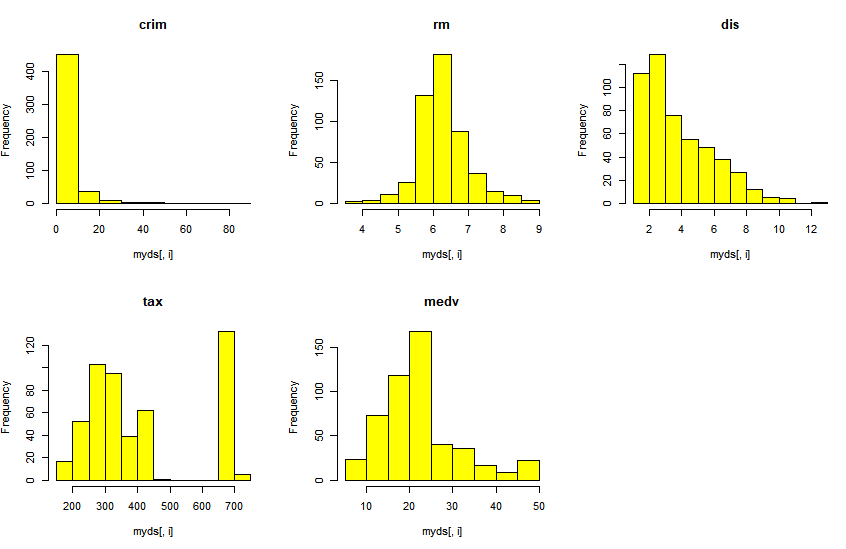
- rm, mdev 변수만 종 모양의 정규분포에 가깝고, crim, dis는 관측 값들이 한쪽으로 쏠려서 분포
- tax는 중간에 관측값이 없는 빈구간이 존재하는 특징
> par(mfrow=c(1,1)) #2X3 가상화면 분할 해제
상자그림에 의한 관측값의 분포 확인
> par(mfrow=c(2,3))
> for(i in 1:5){
+ boxplot(myds[,i], main=colnames(myds)[i])
+ }
> par(mfrow=c(1,1))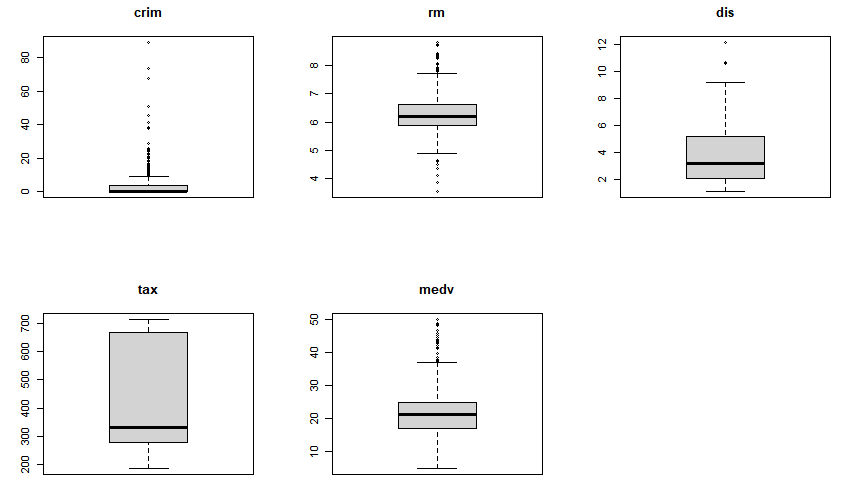
- 1인당 범죄율(crim)은 관측값들이 좁은 지역에 밀집되어 있음(관측값들의 편차가 매우 작음)
- 재산세율(tax)은 넓게 퍼져 있는 것 (관측값들의 편차가 비교적 크다)을 확인
그룹별 관측값 분포의 확인
> boxplot(myds$crim~myds$grp, main="1인당 범죄율")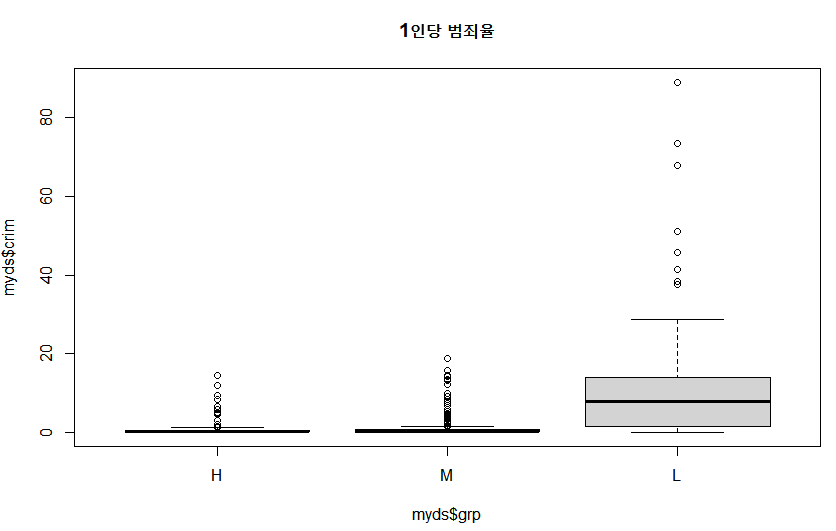
- 주택 가격이 높은 지역이나 중간 지역의 범죄율은 낮고, 주택 가격이 낮은 지역의 범죄율이 높게 나타남
그룹별 관측값 분포의 확인
> boxplot(myds$rm~myds$grp, main="방의 개수")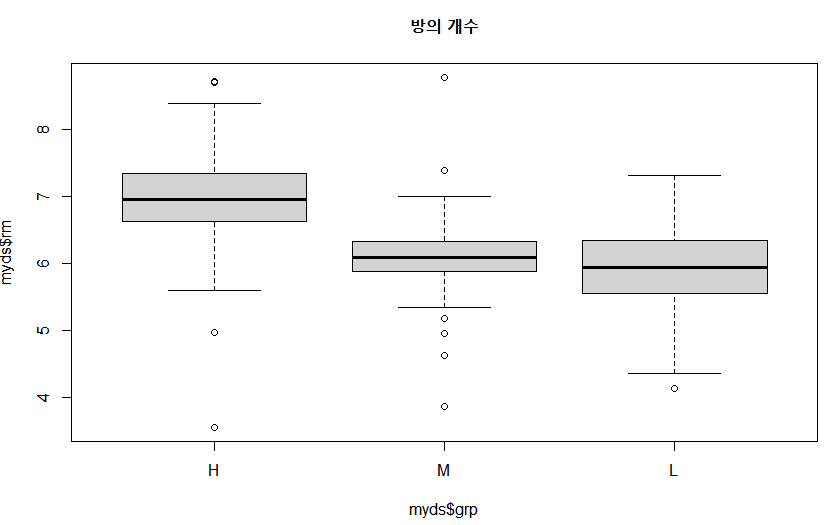
- 주택 가격이 높으면 방의 개수도 많다는 것을 알 수 있음
- 주택 가격이 중간인 지역과 하위인 지역의 방의 개수 평균은 큰 차이가 나지 않음
- 중간 그룹의 방의 개수가 5.2~6.8 사이로 비교적 균일한 반면 하위그룹의 방의 개수는 4.5~7.2 사이로 넓게 펴져 있는 것을 알 수 있음
다중 산점도를 통한 변수 간 상관 관계의 확인
> pairs(myds[,-6])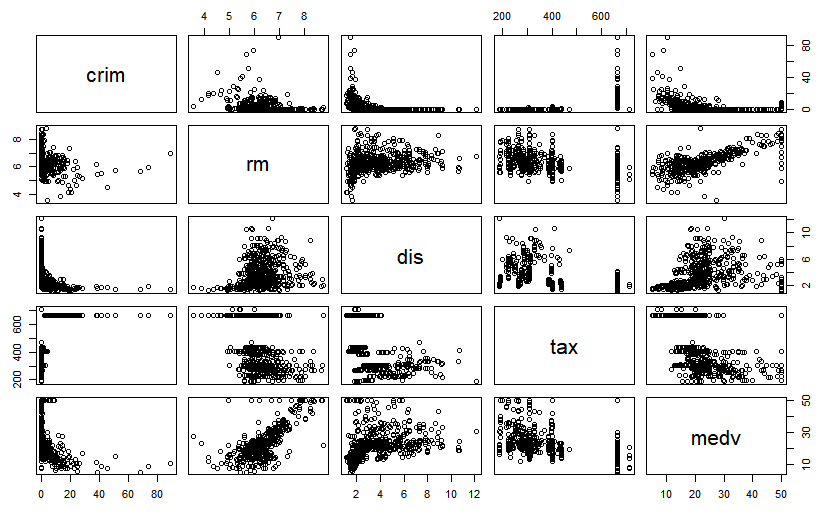
- medv(주택가격)과 양의 상관성이 있는 변수는 rm(가구당 방의 개수)
- crim(1인당 범죄율)은 주택 가격과 음의 상관성이 있는 것으로 보임
그룹 정보를 포함한 변수 간 상관 관계의 확인
> point <- as.integer(myds$grp) #점의 모양 지정
> color <- c("red","green","blue") #점의 색 지정
> pairs(myds[,-6],pch=point, col=color[point])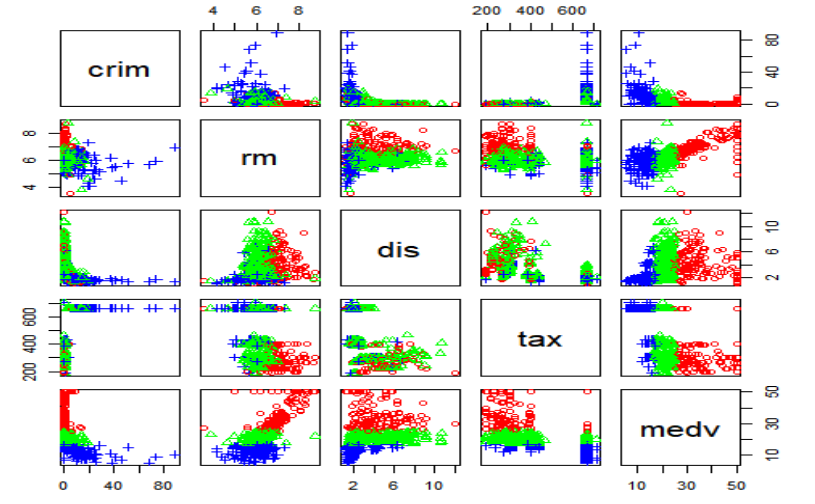
- (crim-medv),(rm-medv),(dis-medvd),(tax-medv) 산점도에서 그룹별로 분포 위치가 뚜렷하게 구분
- 주택 가격 중간 그룹(녹색점들)은 상위 그룹(빨간색), 하위 그룹(파란색)에 비해 주택 가격의 변동폭이 좁음
변수 간 상관계수의 확인
> cor(myds[,-6])
crim rm dis tax medv
crim 1.0000000 -0.2192467 -0.3796701 0.5827643 -0.3883046
rm -0.2192467 1.0000000 0.2052462 -0.2920478 0.6953599
dis -0.3796701 0.2052462 1.0000000 -0.5344316 0.2499287
tax 0.5827643 -0.2920478 -0.5344316 1.0000000 -0.4685359
medv -0.3883046 0.6953599 0.2499287 -0.4685359 1.0000000실습
## (1) Prepare Data
> library(mlbench)
> data("BostonHousing")
> myds <- BostonHousing[,c("crim","rm","dis","tax","medv")]
## (2) Add new column
> grp <- c()
> for(i in 1:nrow(myds)){ #myds$medv 값에 따라 그룹 분류
+ if(myds$medv[i]>=25.0){
+ grp[i] <- "H"
+ } else if (myds$medv[i]<=17.0) {
+ grp[i] <- "L"
+ } else {
+ grp[i] <- "M"
+ }
+ }
> grp <- factor(grp) #문자벡터를 팩터 타입으로 변경
> grp <- factor(grp, levels=c("H","M","L")) #레벨의 순서를 H,L,M -> H,M,L
> myds <- data.frame(myds, grp) #myds에 grp 칼럼 추가
## (3) Add new column
> str(myds)
'data.frame': 506 obs. of 6 variables:
$ crim: num 0.00632 0.02731 0.02729 0.03237 0.06905 ...
$ rm : num 6.58 6.42 7.18 7 7.15 ...
$ dis : num 4.09 4.97 4.97 6.06 6.06 ...
$ tax : num 296 242 242 222 222 222 311 311 311 311 ...
$ medv: num 24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 ...
$ grp : Factor w/ 3 levels "H","M","L": 2 2 1 1 1 1 2 1 3 2 ...
> head(myds)
crim rm dis tax medv grp
1 0.00632 6.575 4.0900 296 24.0 M
2 0.02731 6.421 4.9671 242 21.6 M
3 0.02729 7.185 4.9671 242 34.7 H
4 0.03237 6.998 6.0622 222 33.4 H
5 0.06905 7.147 6.0622 222 36.2 H
6 0.02985 6.430 6.0622 222 28.7 H
> table(myds$grp) #주택 가격 그룹별 분포
H M L
132 247 127
## (4) histogram
> par(mfrow=c(2,3)) # 2x3 가상화면 분할
> for(i in 1:5){
+ hist(myds[,i], main=colnames(myds)[i],col="yellow")
+ }
> par(mfrow=c(1,1)) # 2x3 가상화면 분할 해제
## (5) boxplot
> par(mfrow=c(2,3))
> for(i in 1:5){
+ boxplot(myds[,i], main=colnames(myds)[i])
+ }
> par(mfrow=c(1,1))
## (6) boxplot by group
> boxplot(myds$crim~myds$grp, main="1인당 범죄율")
> boxplot(myds$rm~myds$grp, main="방의 수")
> boxplot(myds$dis~myds$grp, main="직업센터까지의 거리")
> boxplot(myds$tax~myds$grp, main="제산세")
## (7) scatter plot
> pairs(myds[,-6])
## (8) scatter plot with group
> point <- as.integer(myds$grp)
> color <- c("red","green","blue")
> pairs(myds[,-6], pch=point, col=color[point])
## (9) correlation coefficient
> cor(myds[-6])
crim rm dis tax medv
crim 1.0000000 -0.2192467 -0.3796701 0.5827643 -0.3883046
rm -0.2192467 1.0000000 0.2052462 -0.2920478 0.6953599
dis -0.3796701 0.2052462 1.0000000 -0.5344316 0.2499287
tax 0.5827643 -0.2920478 -0.5344316 1.0000000 -0.4685359
medv -0.3883046 0.6953599 0.2499287 -0.4685359 1.0000000