[자료구조와 알고리즘 with Python] Chapter 4 : Tree

김민정·2024년 7월 9일

자료구조와 알고리즘 with Python

목록 보기

4/8

Chapter 4 : Tree (트리)

트리는 나무 모양의 자료구조다.
트리는 계층적인 자료를 아주 쉽게 표현할 수 있고 컴퓨터에서 트리의 응용 분야는 굉장히 다양하다.
자로의 탐색을 위해서도 사용되고, 집합을 나타내는 데도 사용되며 수식을 계산하기 위해서도 사용된다.
트리의 중요한 응용의 하나인 탐색 트리는 추후 Chapter 7에서 다룰 예정이다.

트리는 저장되는 데이터들을 일렬로 나열시키는 것이 아니기 때문에 비선형 자료구조다.

01 "트리란?"

트리는 나무를 닮은 자료구조다.
트리 구조는 계층적인 관계를 가진 자료의 표현에 매우 유용하게 사용된다.

01. 트리 관련 용어

용어	설명
노드 (Node)	각각의 요소들.
간선 (edge)	노드와 노드의 연결 관계를 나타냄.
루트 (root)	계층적인 구조에서 가장 높은 곳에 있는 노드.
부모 노드 (parent node)	간선으로 직접 연결된 노드 중 상위 노드.
자식 노드 (chile node)	간선으로 직접 연결된 노드 중 하위 노드.
형제 노드 (sibling node)	같은 부모를 가진 노드.
조상 노드 (ancestor node)	어떤 노드에서 루트 노드까지의 경로상에 있는 모든 노드.
자손 노드 (descendent node)	어떤 노드 하위에 연결된 모든 노드.
단말 노드 (terminal, leaf node)	자식 노드가 없는 노드. 자식이 있다면 비단말 노드.
노드의 차수 (degree)	노드가 가지고 있는 자식의 수. 단말 노드는 항상 0
트리의 차수	트리에 포함된 모든 노드의 차수 중에서 가장 큰 수
레벨 (level)	트리의 각 층에 번호를 매기는 것. 루트 노드의 레벨은 1이고 한 층씩 내려갈 수록 레벨은 1씩 증가.
트리의 높이 (height)	트리가 가지고 있는 최대 레벨.

트리의 모든 노드는 자신을 루트로 하는 하나의 서브 트리를 대표한다.

02. 트리의 표현 방법

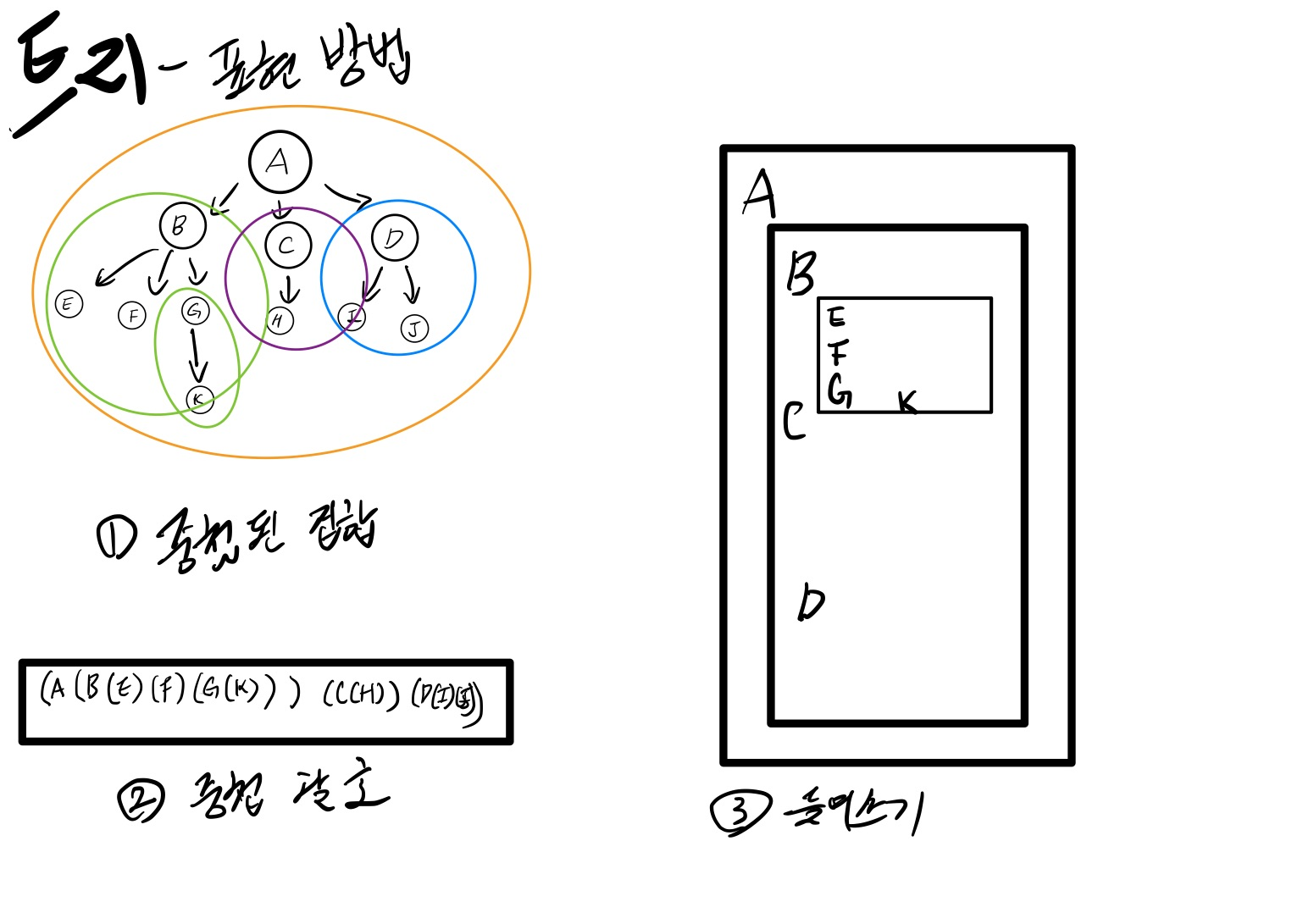
1) 중첩된 집합으로 표현.
2) 중첩된 괄호로 표현.
3) 들여쓰기로 표현.

03. 일반 트리의 표현

자식의 개수에 제한이 없는 트리를 일반 트리라 부른다.

1) N-링크 표현

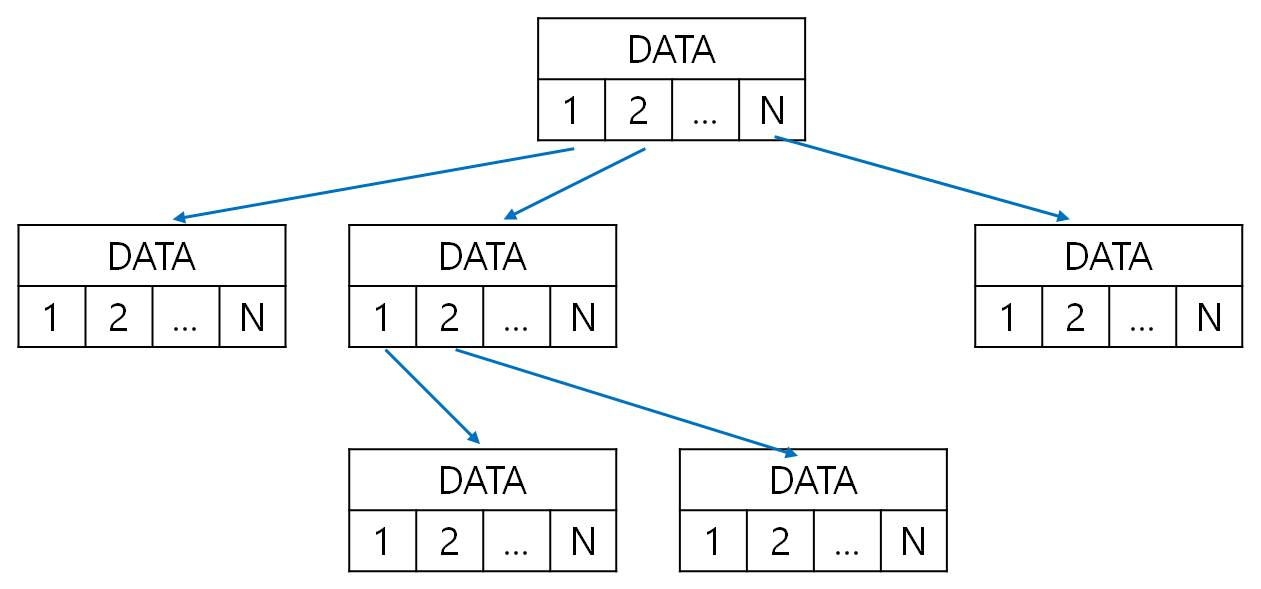
가장 간단한 방법으로 차수가 N인 노드가 N개의 링크를 갖도록 허용하는 것이다.
이 방법은 간단해보이지만 노드마다 링크의 개수가 달라 노드별로 링크를 관리하기 위해 연결 리스트를 사용하고 트리의 표현과 관리가 복잡해진다는 문제가 있다.

2) 왼쪽 자식 - 오른쪽 형제 표현

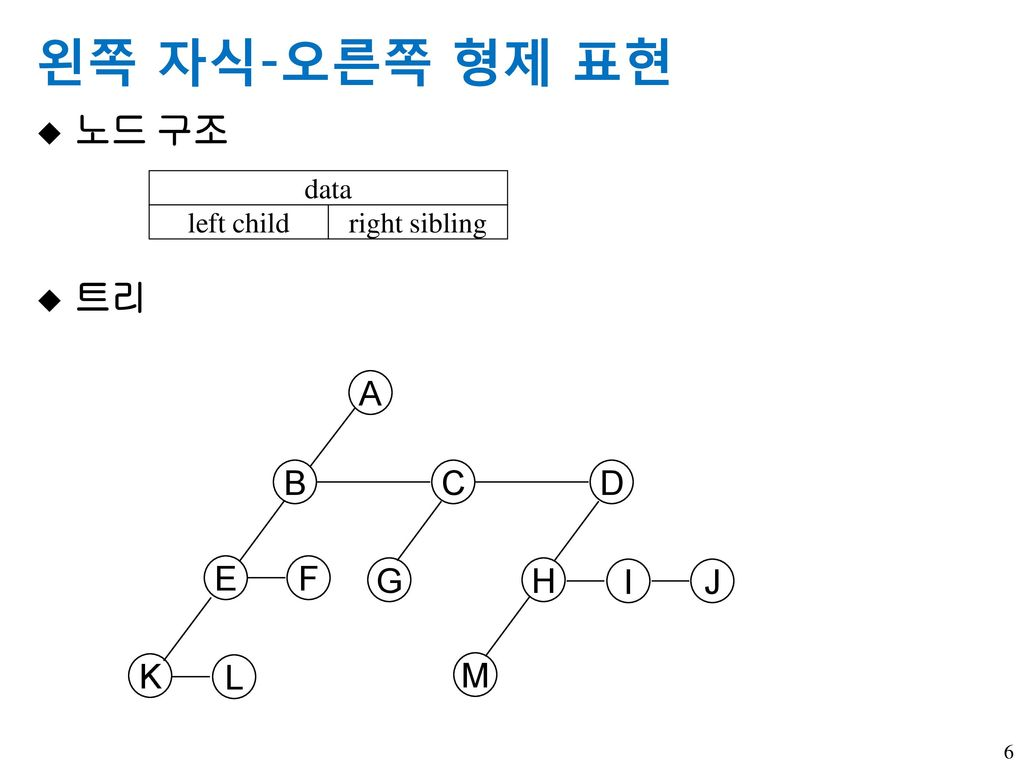
노드가 N개가 아니라 2개의 링크만을 갖도록 하는 방법이다.
하나의 링크는 왼쪽 자식(첫 번째 자식, child)을 가리키고, 다른 하나는 오른쪽 형제(다음 형제, sibling)을 가리키기 위해 사용한다.
형제 노드 사이에도 순서가 있다는 것이 특징이다.

이 방법은 비교적 단순한 형태의 노드를 이용해 임의의 일반 트리를 표현할 수 있다.
다만, 표현이 복잡하고 특히 루트인 A에서 M까지 찾아가는 과정에서 필요 없이 많은 노드를 거쳐야하는 문제가 있다.

다행히 실제로 이 표현을 사용할 때에는 트리 노드의 자식 수에 제한을 두어 비교적 더 단순한 형태의 트리를 많이 사용한다.

02 "이진 트리"

이진 트리 (binary tree)는 모든 노드가 최대 2개의 자식만을 가질 수 있는 트리다.
이때 자식 사이에서도 순서가 존재하는데 왼쪽 자식과 오른쪽 자식은 반드시 구별되어야한다.

이진 트리 구조를 이용해 아주 빠른 자료의 탐색이 가능한 이진 탐색 트리 (binary search tree), 우선 순위 큐를 효과적으로 구현하는 힙 트리 (heap tree), 수식을 트리 형태로 표현하여 계산하는 수식 트리 (expression tree) 등 훌륭한 알고리즘들이 개발되어 있다.

01. 이진 트리 종류

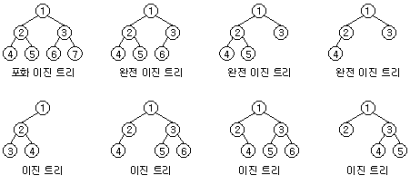
1) 포화 이진 트리 (full binary tree)

트리의 각 레벨에 노드가 꽉 차있는 이진 트리다.
포화 이진 트리는 각 노드의 순서대로 번호를 붙일 수 있다.

2) 완전 이진 트리 (complete binary tree)

마지막 레벨에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진 트리다. 따라서 마지막 레벨에서 노드가 꽉 차 있지 않아도 되지만 중간에 빈 곳이 있으면 안된다.
힙(heap)은 완전 이진 트리의 대표적이 예다.

3) 균형 이진 트리 (balanced binary tree), 높이 균형 이진 트리

모든 노드에서 좌우 서브 트리의 높이 차이가 1 이하인 트리다.
높이가 있는 트리는 경사 트리 또는 경사 이진 트리라 한다.

02. 이진 트리의 표현 방법

1) 배열 구조 표현

이진 트리를 포화 이진 트리의 일부라 생각하면 배열 구조로 트리를 표현할 수 있다.
우선 트리의 높이를 구해 배열(또는 파이썬 리스트)를 할당한다.
예를 들어, 높이가 $k$ 이면 길이가 $(2^k - 1)$ 인 배열이 필요하다.

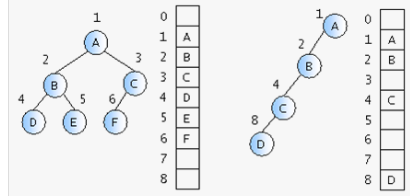
보통 루트 노드의 번호를 1로 하여 계산의 편의를 위해 인덱스 0은 사용하지 않는다.
왼쪽 그림과 같이 포화 이진 트리나 완전 이진 트리에 가장 적합하지만 일반 이진 트리도 표현할 수 있다.
오른쪽 그림과 같이 심한 경사 트리의 경우 배열 항목 사이에 사용하지 않는 빈칸이 많이 발생하여 메모리 낭비가 심해질 수 있다.

이 표현법에서는 어떤 노드의 인덱스를 알면 부모 노드나 자식 노드의 인덱스를 손쉽게 계산할 수 있다.

노드 $i$ 의 부모 노드 인덱스 = $i/2$
노드 $i$ 의 자식 노드 인덱스 = $2i$
노드 $i$ 의 오른쪽 자식 노드 인덱스 = $2i + 1$

2) 연결된 구조 표현: 링크 표현법

연결된 구조로도 이진 트리를 나타낼 수 있는데 이진 트리를 위한 노드는 두 개의 링크가 필요하다. 이 때 좌우 링크는 반드시 구별되어야 하며 각각 왼쪽, 오른쪽 자식 노드를 가리킨다.

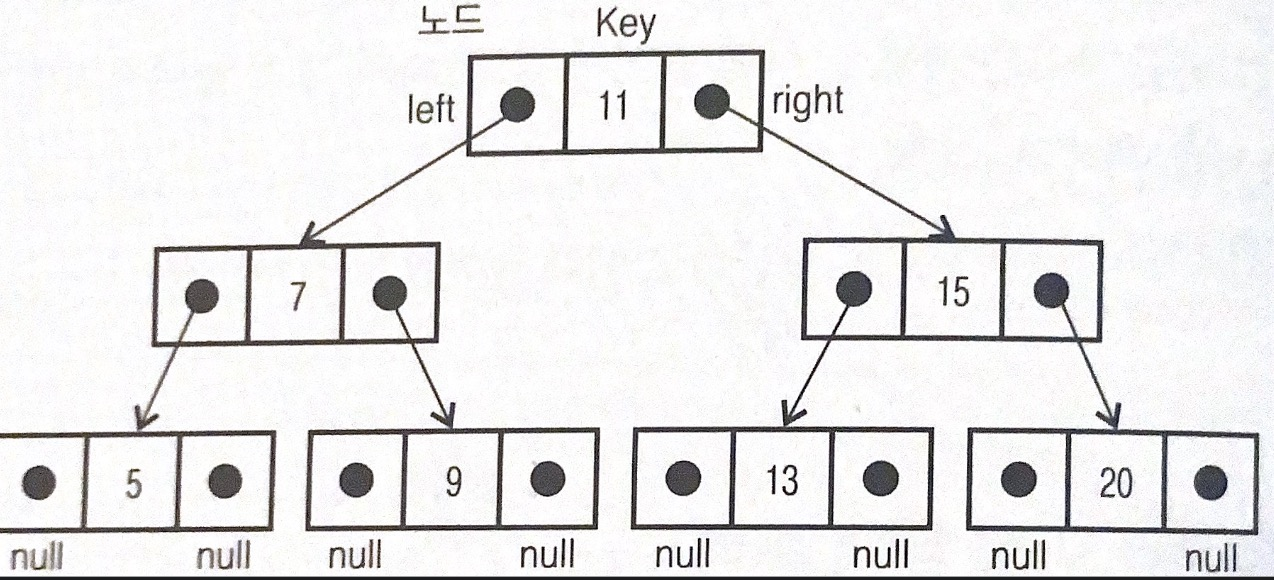
이진 트리를 코드로 구현하자면 아래와 같다.
이번 Chapter에서 다루는 이진 트리 연산들은 아래 코드와 같은 노드를 사용하는 링크 표현법으로 표현되어 있다.

# 코드 4.1: 이진 트리를 위한 노드 클래스
class BTNode:
    def __init__(self, elem, left=None, right=None):
        self.data = elem
        self.left = left
        self.right = right

03 "이진 트리의 연산"

이진 트리는 루트와 2개의 서브 트리로 이루어지는데, 서브 트리도 모두 이진 트리여야 한다는 순환적인 조건이 있다. 이러한 순환적인 특징에 의해 순환 알고리즘이 흔히 사용된다.

01. 이진 트리의 표준순회

트리를 순회(traversal)한다는 것은 트리의 모든 노드를 한 번씩 방문하는 것을 말한다.
예를 들어 트리의 모든 노드를 한 번씩 화면에 출력하기 위해서도 순회가 필요하다. 순회는 모든 자료구조에서 기본적인 연산 중 하나다.

트리에서는 선형 자료구조에 비해 자료가 일렬로 나열되어 있지 않아 여러가지 순서로 노드를 방문할 수 있어 순회 방법이 다양하다.

기본적인 순회 방법은 전위, 중위, 후위 이렇게 세 가지로 나눌 수 있다.

1) 전위순회(preorder) - VLR

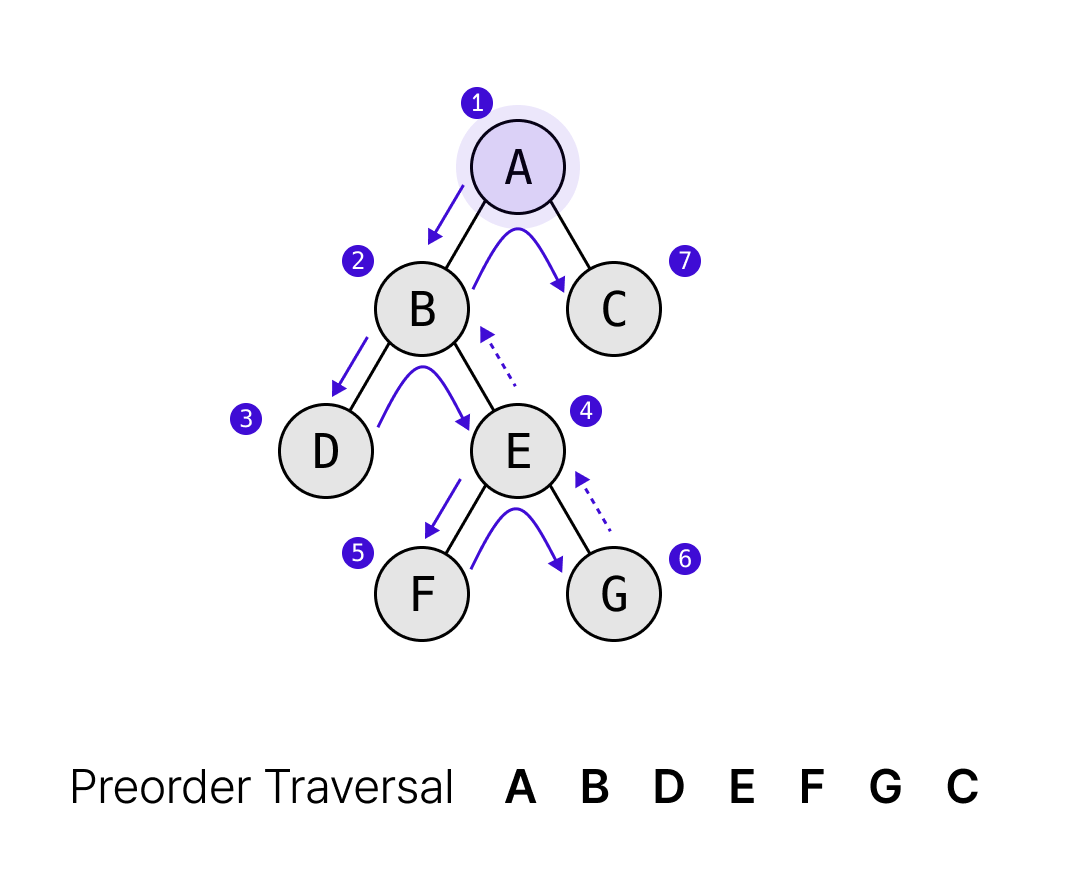
전위순회는 루트(V)를 먼저 방문하고 왼쪽 서브트리(L)를 방문하고, 마지막으로 오른쪽 서브트리(R)를 방문하는 방식이다.

# 코드 4.2: 이진 트리의 전위순회
    def preorder(n):
        if n is not None:
            print("( ", end='')		# 괄호를 추가하여 중첩된 괄호 표현 가능.
            print(n.data, end=' ')
            preorder(n.left)
            preorder(n.right)
            print(") ", end='')		# 괄호를 추가하여 중첩된 괄호 표현 가능.

2) 중위순회(inorder) - LVR

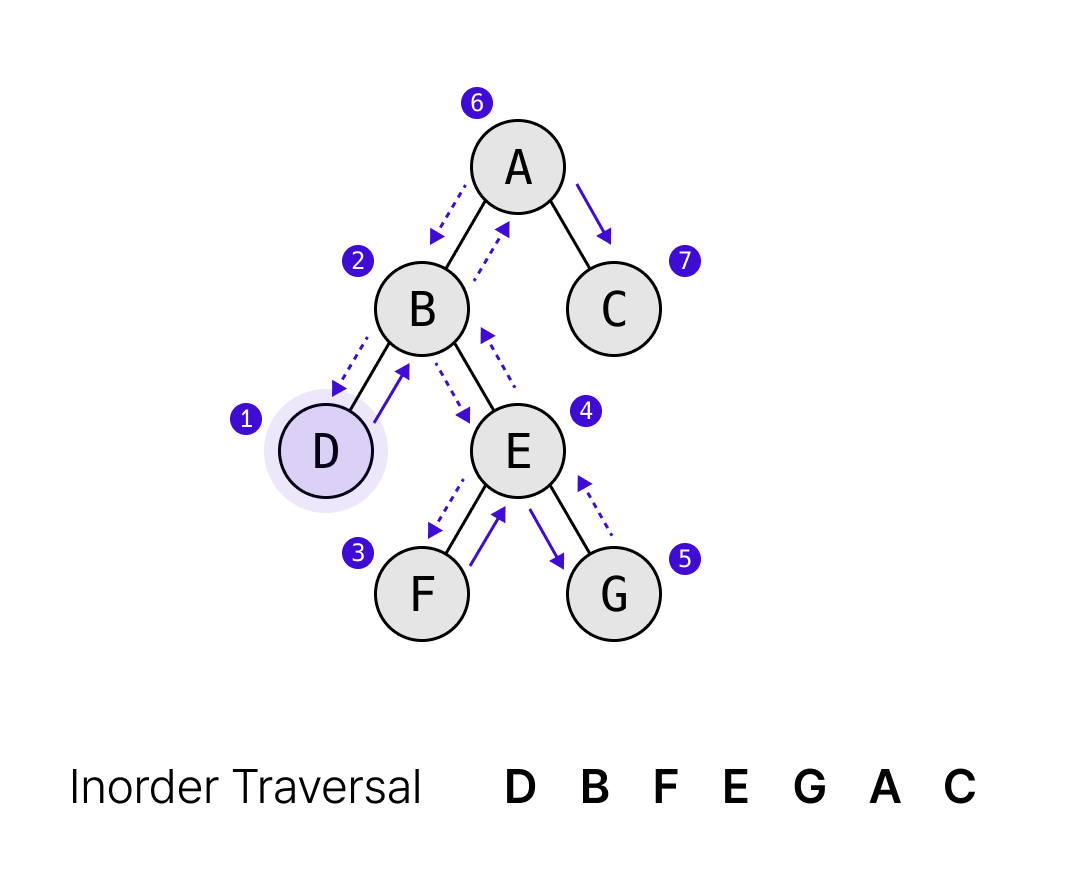
중위순회는 왼쪽 서브트리(L)부터 시작해서 루트(V)를 거쳐 오른쪽 서브트리(R) 순으로 방문하는 방식이다.

# 코드 4.3: 이진 트리의 중위순회
    def inorder(n):
        if n is not None:
            print("( ", end='')		# 괄호를 추가하여 중첩된 괄호 표현 가능.
            inorder(n.left)
            print(n.data, end=' ')
            inorder(n.right)
            print(") ", end='')		# 괄호를 추가하여 중첩된 괄호 표현 가능.

3) 후위순회(postorder) - LRV

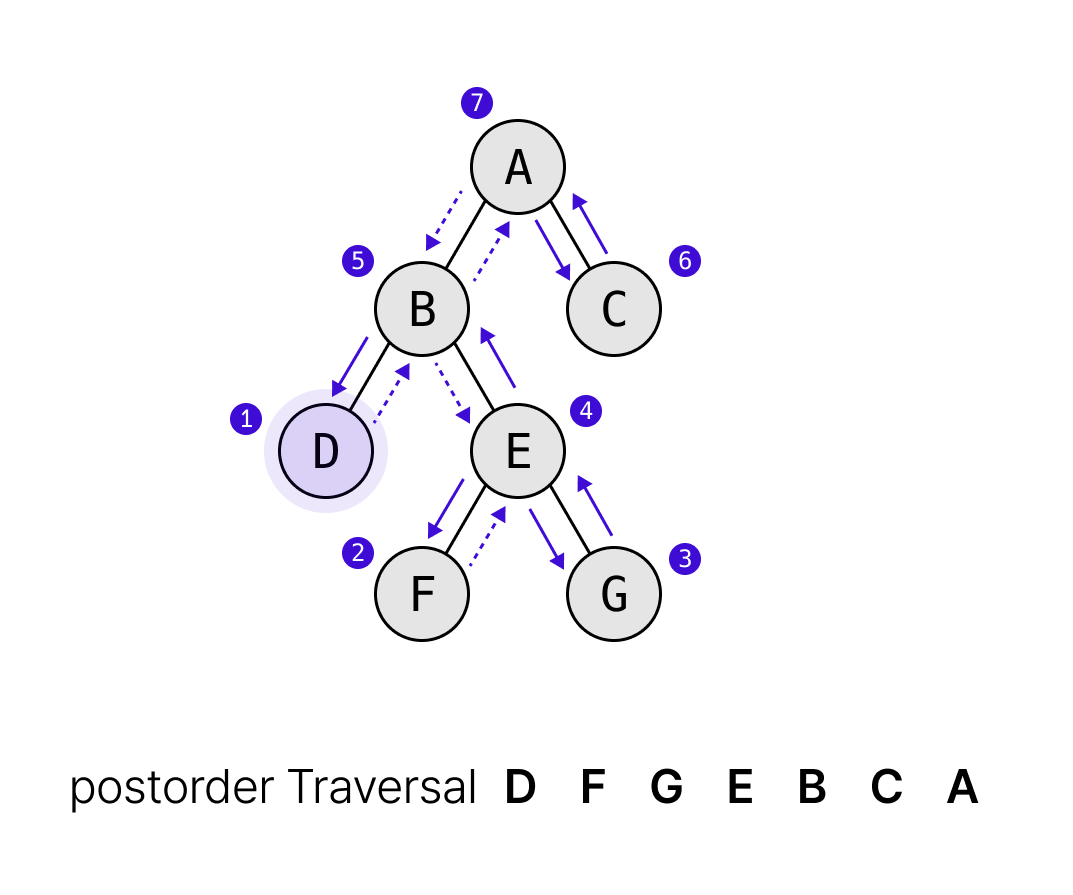
후위순회는 왼쪽 서브트리(L) → 오른쪽 서브트리(R) → 루트(V) 순으로 방문하는 방식이다.

# 코드 4.4: 이진 트리의 후위순회
    def postorder(n):
        if n is not None:
            print("( ", end='')		# 괄호를 추가하여 중첩된 괄호 표현 가능.
            postorder(n.left)
            postorder(n.right)
            print(n.data, end=' ')
            print(") ", end='')		# 괄호를 추가하여 중첩된 괄호 표현 가능.

02. 순회 방법 선택

순서는 중요하지 않고 노드를 전부 방문하기만 한다면 어떤 방법도 상관 없다.
자식을 먼저 처리해야 부모를 처리할 수 있다면 당연히 후위순회를 사용해야 한다.
ex) 어떤 폴더의 용량은 하위 폴더들의 용량을 알아야만 계산할 수 있다.
부모가 처리되어야 자식을 처리할 수 있다면 전위순회를 사용해야 한다.
ex) 모든 노드에서 자신의 레벨을 계산하는 경우, 루트의 레벨이 1이고 나머지 모든 노드는 부모의 레벨보다 1이 크기 때문에 부모의 레벨이 결정되어야 자식의 레벨을 결정할 수 있다.

03. 레벨 순회

레벨 순회는 레벨 순으로 노드를 방문한다.
루트의 레벨은 1이고 아래로 내려 갈수록 레벨이 증가한다. 같은 레벨에서는 왼쪽에서 오른쪽으로 방문한다.
이러한 순서는 큐를 이용하여 간단하게 구현할 수 있다.
큐에 노드를 넣고 빼는 과정을 반복한다.

맨 처음 공백 상태의 큐에 루트를 넣는다. 다음부터는 큐에서 노드 하나를 꺼내 방문할 때마다 해당 노드의 자식들을 큐에 넣는다. 자식을 넣을 때에는 왼쪽 자식 - 오른쪽 자식 순으로 넣는다. 자식이 없다면 삽입하지 않는다. 큐에서 노드가 나오는 순서가 방문 순서다.

# 코드 4.5: 이진 트리의 레벨 순회
    def levelorder(n):
        q = ArrayQueue()
        q.enqueue(root)
        while not q.isEmpty():
            n = q.dequeue()
            if n is not None:
                print(n.data, end=' ')
                q.enqueue(n.left)
                q.enqueue(n.right)

레벨 순회는 트리의 노드를 위 → 아래, 좌 → 우로 출력하므로 표준순회 방법들 보다 출력 결과를 이해하기 조금 쉽다는 장점이 있다.

04. 이진 트리의 연산들

1) 전체 노드 수 구하기

이진 트리의 노드 개수 = 왼쪽 서브 트리의 노드 수 + 오른쪽 서브 트리의 노드 수 + 1(루트 노드)
$N_{total} = N_{left} + N_{right} + 1$

# 코드 4.6: 이진 트리의 노드 수 구하기
    def count_node(n):
        if n is None:
            return 0
        else:
            return 1 + count_node(n.left) + count_node(n.right)

2) 트리의 높이 구하기

이진 트리의 높이 = (왼쪽 서브 트리의 높이와 오른쪽 서브 트리의 높이 중에서 큰 값) + 1
$height = max(h_{left}, h_{right}) + 1$

# 코드 4.7: 이진 트리의 높이 구하기
    def calc_height(n):
        if n is None:
            return 0
        # else:
        #     return 1 + max(calc_height(n.left), calc_height(n.right))
        hLeft = calc_height(n.left)
        hRight = calc_height(n.right)
        if hLeft > hRight:
            return 1 + hLeft
        else:
            return 1 + hRight

3) 테스트 프로그램

해당 테스트 프로그램 코드를 실행할 때 enqueue(), dequeue()를 사용하기 위해선 이전에 작성했던 큐 관련 코드가 필요하다.
👉 <큐의 연산 | 05 "원형 큐의 클래스 구현">

# 코드 4.8: 이진 트리 연산의 테스트 프로그램
d = BTNode('D', None, None)
e = BTNode('E', None, None)
b = BTNode('B', d, e)
f = BTNode('F', None, None)
c = BTNode('C', f, None)
root = BTNode('A', b, c)

print('\n In-order(중위순회) : ', end='')
inorder(root)
print('\n Pre-order(전위순회) : ', end='')
preorder(root)
print('\n Post-order(후위순회) : ', end='')
postorder(root)
print('\n Level-order(레벨순회) : ', end='')
levelorder(root)
print()
print(' 노드의 개수 = %d개'%count_node(root))
print(' 트리의 높이 = %d'%calc_height(root))

> 출력
 In-order(중위순회) : ( ( ( D ) B ( E ) ) A ( ( F ) C ) ) 
 Pre-order(전위순회) : ( A ( B ( D ) ( E ) ) ( C ( F ) ) ) 
 Post-order(후위순회) : ( ( ( D ) ( E ) B ) ( ( F ) C ) A ) 
 Level-order(레벨순회) : A B C D E F 
 노드의 개수 = 6개
 트리의 높이 = 3

04 "모스 코드 결정 트리"

모스 코드(Morse Code)는 도트(점)와 대시(선)의 조합으로 구성된 메시지 전달용 부호다.
모스 코드는 각 알파벳에 대해 점과 선으로 이루어진 코드를 부여했다.

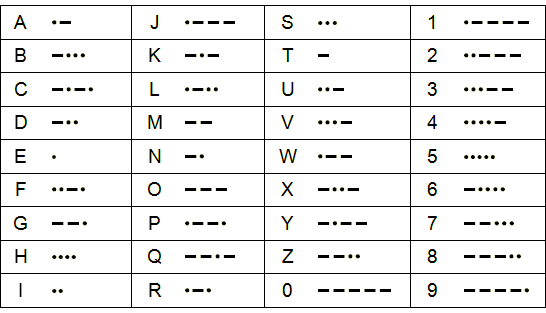
01. 문자를 모스 코드로 변환하는 과정 : 인코딩(encoding)

문자를 모스 코드로 변환하는 것을 부호화 또는 인코딩(encoding)이라 한다.
각 문자열을 모스 코드 표에서 찾아 대응되는 코드를 순서대로 출력하면 된다.

우선, 모스 코드 표를 리스트 table에 저장한다.

# 코드 4.9: 영어 대문자에 대한 모스코드 표
table =[('A', '.-'),    ('B', '-...'),  ('C', '-.-.'),  ('D', '-..'),
        ('E', '.'),     ('F', '..-.'),  ('G', '--.'),   ('H', '....'),
        ('I', '..'),    ('J', '.---'),  ('K', '-.-'),   ('L', '.-..'),
        ('M', '--'),    ('N', '-.'),    ('O', '---'),   ('P', '.--.'),
        ('Q', '--.-'),  ('R', '.-.'),   ('S', '...'),   ('T', '-'),
        ('U', '..-'),   ('V', '...-'),  ('W', '.--'),   ('X', '-..-'),
        ('Y', '-.--'),  ('Z', '--..') ]

다음, 문자가 입력되면 이 문자에 대한 모스 코드를 찾아 반환하는 인코딩 함수다.

# 코드 4.10: 모스코드 인코딩 함수
def encode(ch):
    idx = ord(ch.upper())-ord('A')	# 리스트에서 해당 문자의 인덱스
    return table[idx][1]	# 해당 문자의 모스 부호 반환.

ord()는 파이썬의 내장 함수로 문자를 아스키 코드값으로 바꿔준다. 문자 ch의 아스키 코드값과 'A'의 코드값 차이가 문자 ch의 위치이다.

02. 모스 코드를 문자로 변환하는 과정 : 디코딩(decoding)

이제 반대로 모스 코드가 주어졌을 때 해당하는 알파벳을 추출하는 방법이다. 이 과정을 복호화 또는 디코딩(decoding)이라 한다. 알파벳과 달리 모스코드 위치를 단번에 알기 어렵다.

# 코드 4.11: 단순한 방법의 모스코드 디코딩 함수
def decode_simple(morse):
    for tp in table :               # 모스 코드 표의 모든 문자에 대해
        if morse == tp[1] :         # 찾는 코드와 같으면
            return tp[0]            # 그 코드의 문자를 반환

위와 같이 단순한 방법을 사용한다면 표의 크기(문자 수)가 n개라면 n번 비교해야하기 때문에 매우 비효율 적이다.

03. 결정 트리를 이용한 모스 코드의 디코딩

이진 트리를 이용하면 보다 효율적인 디코딩이 가능하다.
이러한 트리를 결정 트리(decision tree)라 하는데 여러 단계의 복잡한 조건을 갖는 문제에 대해 조건과 그에 따른 해결방법을 트리 형태로 나타낸 것이다.

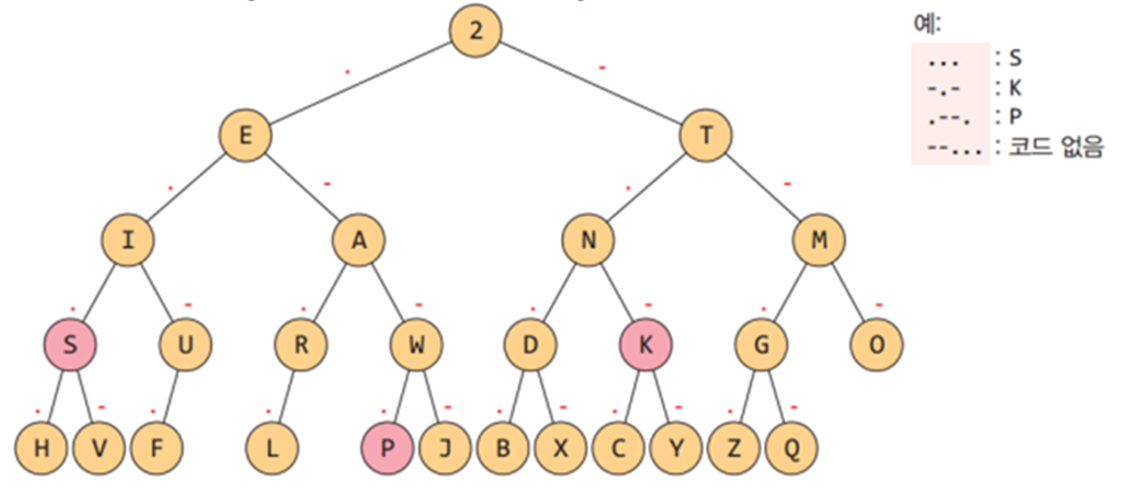
위와 같은 방식으로 결정 트리를 구현할 수 있고 코드로 구현하는 방법은 아래와 같다.

1) 빈 루트 노드를 만들고 모스 코드표의 각 문자를 하나씩 트리에 추가.
2) 문자를 추가할 때 루트부터 시작하여 트리를 타고 내려감. 만약, 타고 내려갈 자식 노드가 None이면 새로운 노드를 추가, 노드만 추가할 뿐이지 그 노드의 문자 아직 결정할 수 없음.
3) 마지막 코드의 노드에 도달하면 그 노드에 문자를 할당.

결정 트리는 이진 트리이므로 노드를 앞에서 사용한 BTNode를 그대로 사용한다.

# 코드 4.12: 모스코드 디코딩을 위한 결정트리 만들기
def make_morse_tree():
    root = BTNode( None, None, None )
    for tp in table :
        code = tp[1]                    # 모스 코드
        node = root                     # 루트부터 탐색
        for c in code :                 # 맨 마지막 문자 이전까지 --> 이동
            if c == '.' :               # 왼쪽으로 이동
                if node.left == None :  # 비었으면 빈 노드 만들기
                    node.left = BTNode (None, None, None)
                node = node.left        # 그쪽으로 이동
            elif c == '-' :             # 오른쪽으로 이동
                if node.right == None : # 비었으면 빈 노드 만들기
                    node.right = BTNode (None, None, None)
                node = node.right     # 그쪽으로 이동

        node.data = tp[0]               # 코드의 알파벳
    return root

결정 트리가 만들어지면 이제 효율적인 디코딩이 가능하다.

# 코드 4.13: 결정트리를 이용한 디코딩 함수
def decode(root, code):
    node = root
    for c in code :                 # 맨 마지막 문자 이전까지 --> 이동
        if c == '.' :
            node = node.left        # 왼쪽으로 이동
        elif c=='-' :
           node = node.right        # 오른쪽으로 이동
    return node.data

결정 트리가 n개의 노드를 갖는 포화 이진 트리라면 높이가 $log_{2}n$ 이 되는데 이 디코딩 함수는 $log_{2}n$ 에 비례하는 비교가 필요하다.

04. 테스트 프로그램

문자열을 받아 모스 코드로 바꾸고, 이 코드를 다시 문자열로 복구하는 테스트 프로그램이다.

# 코드 4.14: 인코딩과 디코딩 테스트 프로그램
morseCodeTree = make_morse_tree()
str = input("입력 문장 : ")
mlist = []
for ch in str:
    code = encode(ch)
    mlist.append(code)
print("Morse Code: ", mlist)
print("Decoding  : ", end='')
for code in mlist:
    ch = decode(morseCodeTree, code)
    print(ch, end='')
print()

> 출력
입력 문장 : HELLO
Morse Code:  ['....', '.', '.-..', '.-..', '---']
Decoding  : HELLO

입력 문장 : GAMEOVER
Morse Code:  ['--.', '.-', '--', '.', '---', '...-', '.', '.-.']
Decoding  : GAMEOVER

05 "수식 트리"

$(3 * 4 ) + ( 6 - 8)$

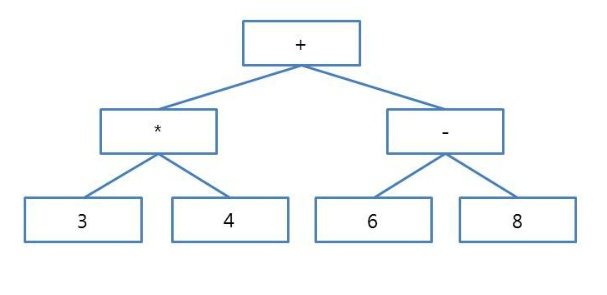
수식 트리(Expression Tree)란 산술식을 트리 형태로 표현한 이진 트리다.
수식 트리는 하나의 연산자가 두 개의 피연산자를 갖는다고 가정하는데 피연산자는 단말노드에 저장되고 연산자는 루트나 가지노드에 배치한다.

01. 수식 트리의 계산

수식 트리에 저장된 식을 계산하는 방법에 대해 살펴보자.
어떤 연산자를 계산하려면 자식 노드의 계산이 반드시 끝나야 한다.
따라서, 수식 트리의 계산에는 후위순회가 사용된다.
자식 노드을 먼저 처리해야지 부모 노드를 처리할 수 있기 때문이다.

이제 문자열로 수식을 입력하면 수식 트리로 만들어 루트 노드를 반환하는 함수를 만들 것이다.

02. 수식의 표현 방법

수식은 연산자와 피연산자(상수, 미지수)로 이루어지는데, 이들은 상대적인 위치에 따라 몇 가지 방법으로 구분할 수 있다.

전위(prefix)	중위(infix)	후위(postfix)
연산자-피연산자1-피연산자2	피연산자1-연산자-피연산자2	피연산자1-피연산자2-연산자
+ A B	A + B	A B +
+ 5 * A B	5 + A * B	5 A B * +

전위 표기법 : 연산자를 먼저 적고 좌우 피연산자를 이어서 적는 방법.
후위 표기법 : 연산자를 중간 또는 마지먹에 적는 방법.
중위 표기법 : 피연산자와 연산자를 번갈아 적는, 우리에게 익숙한 표기법.

컴퓨터가 수식을 이해할 땐 연산자들 사이의 우선순위를 처리하기 위해 후기 표기법을 사용한다.

※ 후기 표기법의 장점.
1) 괄호를 사용하지 않아도 계산 순서를 알 수 있다.
ex) ( A + B ) C → A B + C
2) 연산자의 우선순위를 생각할 필요가 없다. 식 자체에 우선순위가 이미 포함되어 있다.
ex) A + B C → B C A +
3) 수식을 읽으면서 바로 계산할 수 있다. 중위 표기는 괄호와 연산자의 우선수위 때문에 끝까지 식을 읽은 다음에 계산할 수 있다.

우리에게 익숙한 중위표기를 후위표기 수식으로 변환한 다음 식을 계산하는 방법은 흔히 사용되는데 이 과정을 모두 스택으로 나타낼 수 있다.

03. 수식 트리 만들기

전위표기와 후위표기로 기술된 수식을 자동으로 수식 트리로 바꾸는 방법에 대해 알아보자.

1) 전위표기 식으로 수식 트리 만들기.
: 맨 앞에서 뒤로 읽으면서 처리.

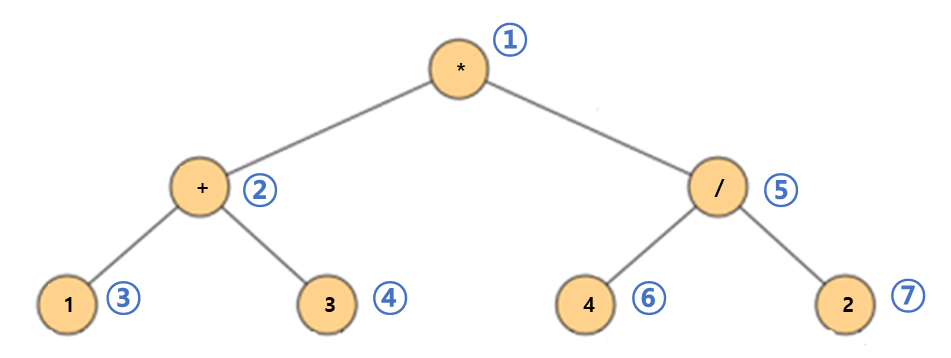
입력 수식 : * + 1 3 / 4 2
1. 첫 항목 *은 수식 트리의 루트 노드가 된다.
2. +의 이전 항목이 연산자 * 이므로 +는 *의 왼쪽 자식이 된다.
3. 1은 이전 항목이 다시 연산자 + 이므로 1은 +의 왼쪽 자식이 된다.
4. 3은 이전 항목이 피연산자이므로 3은 이전 연산자 +의 두 번째 피연산자가되어 +를 루트로 하는 오른쪽 자식이 된다.
5. +가 루트인 서브 트리는 다 찼으므로 이제 /연산자는 * 연산자의 오른쪽 자식이 된다.
6. 4는 이전 연산자 /의 왼쪽 자식이 된다.
7. 2는 이전 연산자 /의 오른쪽 자식이 된다.

# 코드 4.15: 전위표기 수식을 이용한 수식 트리 계산 함수
def evaluate(node):
    if node is None:    # 공백 트리면 0 반환
        return 0
    elif node.isLeaf(): # 단말 노드면 -> 피연산자 (상수, 미지수)
        return node.data    # 그 노드 값(데이터) 반환
    else:   # 루트나 가지노드라면 -> 연산자
        nd1 = evaluate(node.left)
        nd2 = evaluate(node.right)
        if node.data == '+':    # 루트(현재 노드)를 후위 순회로 처리.
            return nd1 + nd2
        elif node.data == '-':
            return nd1 - nd2
        elif node.data == '*':
            return nd1 * nd2
        elif node.data == '/':
            return nd1 / nd2

2) 후위표기 식으로 수식 트리 만들기.
: 맨 뒤에서 앞으로 읽으면서 처리.

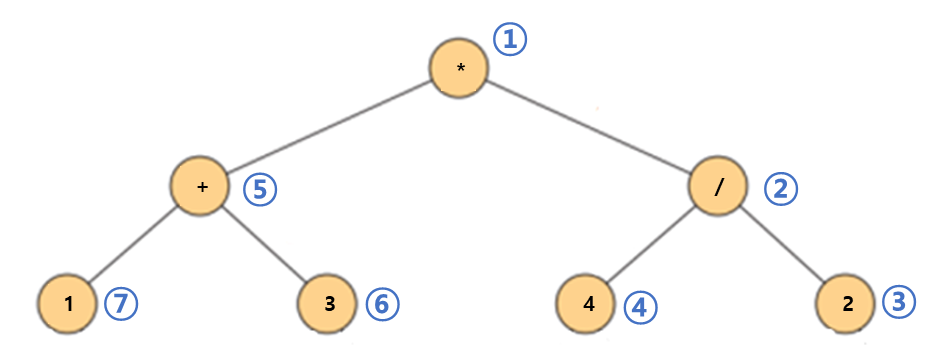
입력 수식 : 1 3 + 4 2 / *
1. 첫 번째 연산자 *은 수식 트리의 루트 노드가 된다.
2. /은 이전 항목이 연산자 *이므로 /는 *의 오른쪽 자식이 된다.
3. 2는 이전 항목이 다시 연산자 /이므로 2는 /의 오른쪽 자식이 된다.
4. 4는 이전 항복이 피연산자이므로 4는 이전 연산자 /의 두 번째 피연산자가 되어 /를 루트로 하는 오른쪽 자식이 된다.
5. /가 루트인 서브 트리는 다 찼으르모 이제 + 연산자는 * 연산자의 왼쪽 자식이 된다.
6. 3은 이전 연산자 +의 오른쪽 자식이 된다.
7. 1은 이전 연산자 +의 왼쪽 자식이 된다.

# 코드 4.16: 후위표기 수식을 이용한 수식 트리 만들기.
def buildETree(expr):
    if len(expr) == 0:
        return None

    token = expr.pop()  # 후위표기 수식은 후위순회로 맨 뒤에 있는 요소 꺼냄.
    if token in "+-*/": # 연산자일 경우 노드를 만들고, 왼쪽순으로 서브트리를 순환 호출을 이용해 만듦.
        node = BTNode(token)
        node.right = buildETree(expr)
        node.left = buildETree(expr)
        return node
    else:
        return BTNode(float(token)) # 피연산자이면 단말노드이므로 노드를 바로 만들어 반환.

04. 테스트 프로그램

# 코드 4.17: 수식 트리 테스트 프로그램
str = input("입력(후위표기): ") # 후위표기식 입력
expr = str.split()
print("토큰분리(expr): ", expr)
root = buildETree(expr) # 후위표기식을 수식트리로 만들고 루트 반환
print("\n전위순회: ", end='');
preorder(root)
print("\n중위순회: ", end='');
inorder(root)
print("\n후위순회: ", end='');
postorder(root)
print("\n계산 결과: ", evaluate(root))  # 수식 트리 계산

> 출력
입력(후위표기): 1 3 + 4 2 / *
토큰분리(expr):  ['1', '3', '+', '4', '2', '/', '*']

전위순회: * + 1.0 3.0 / 4.0 2.0 
중위순회: 1.0 + 3.0 * 4.0 / 2.0 
후위순회: 1.0 3.0 + 4.0 2.0 / * 
계산 결과: 8.0

후기

트리는 앞에서 다룬 자료구조와 달리 비선형, 계층적인 성격을 띄다보니 자료를 읽는 방법이 다양했고 과정도 꽤나 순서가 명확히 있는 느낌이라 스도쿠 퍼즐 풀듯이 배울 수 있던거 같다.╰(*°▽°*)╯

앞으로 정렬, 탐색, 그래프 와 같은 알고리즘 관련 자료구조도 배울 텐데 기대가 된다~!

김민정

백엔드 코린이😁

이전 포스트

[자료구조와 알고리즘 with Python] Chapter 3 : List

다음 포스트

[자료구조와 알고리즘 with Python] Chapter 4 : Tree