[자료구조와 알고리즘 with Python] Chapter 5 : Algorithm

김민정·2024년 7월 11일

자료구조와 알고리즘 with Python

목록 보기

5/8

Part 2 : Algorithm

chapter 5에서 알고리즘 정의를 알아보고, 어떤 알고리즘이 더 좋은지 평가하는 방법에 대해 알아본다.
chapter 6~7에서는 컴퓨터 분야에서 가장 중요한 문제인 정렬과 탐색에 대한 유명한 알고리즘인 정렬, 탐색에 대해 알아본다.
chapter 8에서는 가장 복잡한 관계를 표시할 수 있는 그래프의 개념과 관련 알고리즘들을 다룰 예정이다.

Chapter 5 : Algorithm (알고리즘 개요)

이번 챕터에서는 알고리즘이 무엇이고, 알고리즘은 어떻게 표현할 수 있는지, 알고리즘의 성능을 평가하는 방법에 대해 다룬다. 어떤 문제를 해결하는 다양한 알고리즘이 있을 때, 이들을 서로 비교하고 어떤 것이 더 좋은지를 판단할 수 있는 능력을 길러보자.

01 "알고리즘이란?"

01. 알고리즘의 정의와 조건

알고리즘(algorithm)은 주어진 문제를 해결하기 위한 단계적인 절차를 말한다.
컴퓨터에서는 어떤 일을 하는 절차를 표현하기 위해 명령어들을 사용하는데 결국 알고리즘은 특정한 일을 수행하는 명령어들의 집합으로 볼 수 있다.
명령어(instruction set)란 컴퓨터에서 수행되는 문장들을 의미하고 C언어나 Java, Python 등과 같은 프로그래밍 언어와 상관없이 문제 해결 절차를 나타내는 명령어의 집합이다.

그렇다고 프로그래밍을 위해 작성된 모든 명령어의 집합이 알고리즘이 되는 것은 아니며 다음과 같은 조건들을 만족해야한다.

알고리즘의 조건
1. 입력: 모호하지 않고 잘 정의된 입력
2. 출력: 명확히 정의된 1개 이상의 출력
3. 명확성: 각 명령어의 의미가 모호하지 않고 명확해야 함
4. 유한성: 한정된 수의 단계 후에는 반드시 종료되어야 함
5. 언어 독립성: 프로그래밍 언어와 상관 없음
6. 유효성: 명령어들은 현재 실행 가능한 연산이어야 함

02. 알고리즘의 기술 방법

영어나 한국어와 같은 자연어를 사용하는 방법
흐름도(flowchart)로 표시하는 방법.
특정한 프로그래밍 언어(C언어, Java, Python)의 코드로 나타내는 방법
유사 코드로 기술하는 방법

01) 자연어 표현
: 자연어를 사용하면 표현이 자유롭고 편리하다는 장점이 있지만, 자칫 문장의 의미가 애매해질 수 있다는 단점이 있다.

# 코드 5.1: 세 개의 숫자에서 최댓값을 찾는 알고리즘 - 자연어 표현
find_max(a, b, c)
    a를 최댓값을 저장하는 변수 max에 복사합니다.
    만약 b가 max보다 크면 b를 max에 복사합니다.
    만약 c가 max보다 크면 c를 max에 복사합니다.
    max를 반환합니다.

02) 흐름도 표현
: 흐름도(flowchart)는 알고리즘의 절차들을 가장 정확하게 표현할 수 있어 특허 명세서 등에서 많이 사용된다. 하지만 알고리즘이 조금만 길어도 그림이 너무 복잡해져 혼란스러워진다는 문제가 있다.

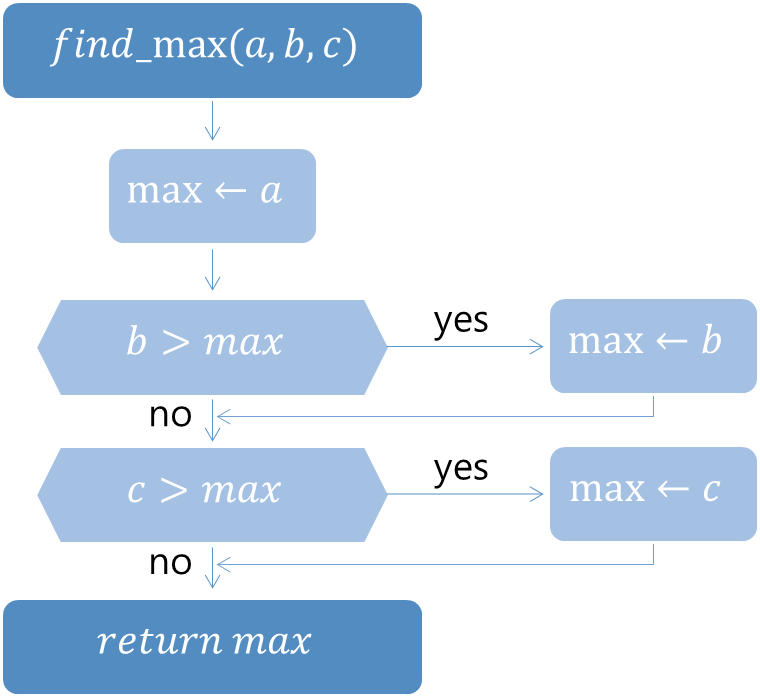
03) 특정 프로그래밍 언어 표현
: 특정 프로그래밍 언어로 기술하면 알고리즘을 실행해 볼 수 있어 편리하다.
하지만 프로그래밍 언어의 문법을 정확히 따라 기술해야 하고 언어의 특징에 따른 많은 불필요한 표현들이 알고리즘에 포함된다는 문제가 있다.
따라서 간단한 알고리즘도 복잡해보일 수 있고 이것이 알고리즘의 핵심을 이해하는 것을 방해한다는 문제가 있다.

# 코드 5.2: 세 개의 숫자에서 최댓값을 찾는 알고리즘 - C언어로 표현
int find_max(int a, int b, int c)
{
    int max = a;
    if (b > max)
        max = b;
    if (c > max)
        max = c;
    return max;
}

04) 유사코드(pseudo code) 표현

유사코드는 자연어보다는 체계적이지만 프로그래밍 언어보다는 덜 엄격한 방법이다.
특히, 프로그래밍 언어에서 발생하는 많은 불필요한 표현을 생략할 수 있어 논문이나 도서들에서 흔히 사용된다.
유사코드의 문법은 C와 같은 기존 언어들과 유사하지만, 대입(할당) 연산자로 =이 아니라 ←를 사용하고 =는 비교연산자로 사용된다.

# 코드 5.3: 세 개의 숫자에서 최댓값을 찾는 알고리즘 - 유사코드 표현
find_max(a, b, c)
    max <- a
    if b > max then
        max <- b
    if c > max then
        max <- c
    return max

05) Python을 이용한 표현

python 코드는 유사코드 표현과 매우 유사하다.
python은 알고리즘을 바로 실행하여 결과를 확인할 수 있다는 장점이 있다.

def find_max(a, b, c):
    max = a
    if b > max:
        max = b
    if c > max:
        max = c
    return max

02 "알고리즘의 성능 분석"

알고리즘의 성능 분석 기준은 2가지가 있다.

연산량 (시간 효율성)
: 알고리즘이 얼마나 적은 연산을 수행하는가? → 시간 복잡도

메모리 사용량 (공간 효율성)
: 알고리즘이 얼마나 적은 메모리 공간을 사용하는가? → 공간 복잡도

예전과 달리 요즘은 컴퓨터에 메모리가 풍부해졌고 이 둘을 동시에 만족시키기는 쉽지 않기 때문에 둘 중 하나 고르라면 보통 시간 효율성을 선택한다.

01. 실행 시간 측정 방법

시간 효율성을 측정하는 방법 중 단순하지만 가장 확실한 것은 실행 시간을 직접 측정하는 것이다. 파이썬에서는 time모듈을 사용해 확인할 수 있다.
아래 예시는 testAlgorithm()함수의 실행 시간을 측정한다.

# 코드 5.5: time 모듈을 이용한 실행시간 측정 예
import time
start = time.time()
testAlgorithm(input)
...
end = time.time()
print('실행시간 = ', end - start)

이런 방법으로 시간 효율성을 측정하면 치명적인 약점이 있다.

알고리즘을 반드시 '구현'해야한다.
: 알고리즘이 비교적 단순하다면 어렵지 않게지만 복잡한 경우 구현이 큰 부담이 될 수 있다.
여러 알고리즘의 측정 결과를 비교하기 위해선 같은 조건의 하드웨어를 사용해야한다.
: 실행 속도 (슈퍼 컴퓨터 << 스마트폰)
소프트웨어 환경(프로그래밍 언어, 운영체제)도 같아야 한다.
: 실행 속도 (C / C++의 컴파일 방식 << Python / Basic의 인터프리트 방식)
성능 비교에 사용했던 데이터가 아닌 다른 데이터에 대해서는 전혀 다른 결과가 나올 수 있으므로 실험되지 않은 입력에 대해서는 실행 시간이 불확실하다.

02. 복잡도 분석 방법

알고리즘을 구현하지 않고도 복잡도 분석(coplexity analysis)을 이용하여 시간 복잡도(time complexity), 공간 복잡도(space coimplexity)를 구해 성능을 비교할 수 있다.

# 코드 5.6: 1부터 n까지 합을 구하는 알고리즘 - 반복문 이용
cal_sum1(n)
    sum <- 0
    for i <- 1 to n then    # 반복문
        sum <- sum + i
    return sum

이를 1부터 n까지 합 공식을 이용하면 아래와 같이 나타낼 수 있다.

# 코드 5.7: 1부터 n까지 합을 구하는 알고리즘 - 합 공식 이용
cal_sum2(n)
    sum <- n * (n + 1) / 2
    return sum

위 두 개의 알고리즘 성능을 비교해보자.
알고리즘의 복잡도를 구하기 위해서는 각 알고리즘에서 얼마나 연산이 실행되었는지 $T(n)$ , 복잡도 함수를 사용하는데, 이는 연산의 실행 횟수를 입력의 크기 n에 대한 함수의 형태를 나타낸다.

알고리즘 1 (반복문 이용)
$T_1(n) = 2n + 1$
: 반복문이 $n$ 번 수행되는데 대입과 연산을 한번씩 수행한다. ( $2n$ )
이 외 대입이 한번 진행되므로 위와 같은 복잡도 함수를 얻을 수 있다. ( $+1$ )
알고리즘 2 (합 공식 이용)
$T_2(n) = 4$
: n값에 상관없이 대입, 곱셈, 덧셈, 나눗셈 연산이 한번씩 수행되므로 위와 같은 복잡도 함수를 얻을 수 있다. ( $4$ )

그래프로 생각하면 1차 함수와 상수 함수므로 미지수 n의 값이 커질 수록 기울기가 큰 알고리즘 1이 알고리즘 2에 비해 비효율적이라는 것을 알 수 있다.

03. 복잡도의 점근적 표기

알고리즘 복잡도를 함수로 나타냈을 때 최고차항의 상수와 이외 항들을 모두 소거하고 최고차항 끼리만 겨뤄 비교하는 편이다. (그 외에 항들은 연산 횟수(n)가 기하학적으로 커졌을 때 무의미해지기 때문)
이러한 표현 방법을 점근적 표기(asymptotic notation)이라 한다.
점근적 표기에 상한과 하한 및 동일 등급과 같은 개념을 적용하면 빅오 표기법, 빅오메가 표기법으로 나눌 수 있고 빅세타 표기법도 있다.

1) 빅오(Big-O) 표기법
$O(g(n)$ 은 증가속도가 $g(n)$ 과 같거나 낮은 모든 복잡도 함수를 포함하는 집합이다.
예를 들면 알고리즘의 복잡도가 $O(n^2)$ 라면 이 알고리즘은 어떤 경우에도 $n^2$ 에 비례하는 시간 안에 반드시 완료된다는 것을 말한다.
이것은 처리시간의 상한(upper bound)을 의미한다.
아까 구한 알고리즘 1의 복잡도 함수는 ' $O(n)$ 에 속한다' 또는 ' $O(n)$ 이다'라고 말할 수 있고 $O(n^2)$ 에도 포함될 수 있다.

2) 빅오메가(Big-Omega) 표기법
$Ω(g(n))$ 은 증가속도가 $g(n)$ 과 같거나 높은 모든 복잡도 함수를 포함한다.
이것은 복잡도의 하한(lower bound)을 의미한다.
예를 들면 $Ω(n^2)$ 은 아무리 빨리 처리하더라도 $n^2$ 에 비례하는 시간 이상은 반드시 걸린다는 것이다.

3) 빅세타(Big-Theta) 표기법
$Θ(g(n)$ 은 증가속도가 $g(n)$ 과 같은 복잡도 함수들만 포함한다. 이것은 상한인 동시에 하한인 경우다.

만약 시간 복잡도를 정확히 계산할 수 있다면 빅세타 표기법을 사용하는 것이 좋고, 일반적으로는 최악의 상황을 고려한 해결책을 찾기 때문에 빅오 표기법을 사용한다.
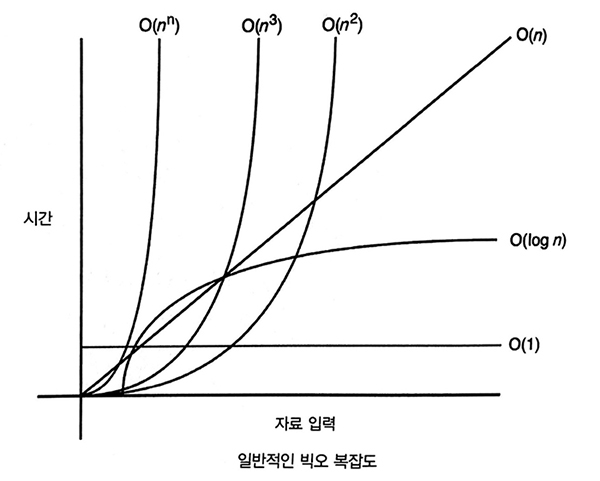
빅오 표기 수행시간을 순서대로 나열하면 아래와 같다.

$O(1)$ < $O(logn)$ < $O(n)$ < $O(nlogn)$ < $O(n^2)$ < $O(n^3)$ < $O(2^n)$ < $O(3^n)$ < $O(n!)$

04. 최선 최악, 평균적인 효율성

알고리즘의 효율성은 입력의 특징에 따라 3가지의 경우로 나누어 평가할 수 있다.

최선의 경우(best case)
: 실행 시간이 가장 적은 경우. 알고리즘 분석에서는 큰 의미 X

평균적인 경우(average case)
: 알고리즘의 모든 입력을 고려하고 각 입력이 발생활 확률을 고려한 평균적인 실행 시간을 의미. 정확한 계산 어렵다.

최악의 경우(worst case)
: 입력의 구성이 알고리즘의 실행 시간을 가장 많이 요구하는 경우. 가장 중요하게 사용됨.

두 가지 알고리즘을 예로 들어본다.

리스트에서 최댓값을 찾는 알고리즘
리스트에서 어떤 값을 찾는 알고리즘

1) 리스트에서 최댓값을 찾는 알고리즘

# 코드 5.8: 리스트에서 최댓값을 찾는 알고리즘
def find_max(a):
    n = len(a)
    max = a[0]
    for i in range(n):
        if a[i] > max:
            max = a[i]
    return max

위 알고리즘의 복잡도 함수는 $T(n) = n$ 으로 $O(n)$ 에 속한다.

2) 리스트에서 어떤 값을 찾는 알고리즘
어떤 값을 찾으려고 한다면 리스트(a) 요소 하나하나 탐색하는 순차 탐색을 해야한다.

# 코드 5.9: 리스트에서 어떤 값을 찾는 알고리즘
def find_key(a, key):
    n = len(a)
    for i in range(n):
        if a[i] == key:
            return i
    return -1

위 알고리즘의 경우 입력의 구성에 따라 검사 횟수가 달라지므로 최선, 최악, 평균을 나누어 분석해야한다.

최선의 경우
: 첫 번째 요소가 찾는 값일 경우.
$T_{best}(n) = 1 ∈ O(1)$
최악의 경우
: 찾는 값이 리스트의 맨 뒤에 있거나 없는 경우.
$T_{worst}(n) = n ∈ O(n)$
평균적인 경우
: 각 숫자를 찾게 될 가능성이 $1/n$ 으로 동일하다고 가정한다면 각 숫자를 탐색했을 때 비교 연산의 횟수를 모두 더한 다음 이것을 전체 숫자의 개수로 나눠주면 평균적인 경우의 비교 연산 수행 횟수를 계산할 수 있다.
$T_{avg}(n) = {n+1 \over 2} ∈O(n)$
평균적인 경우는 계산하기 어려운 경우가 많고, 최악의 상황에 대한 시간을 보장 못한다는 점에서 문제점이 있다.
그래서 대부분 최대한 불리한 입력 데이터를 사용하는 최악의 경우에 대한 복잡도가 가장 중요하다.✨