
Chapter 7: 탐색 (Search)
이번 Chapter에서는 기본적인 탐색 알고리즘들과 함께 이진 트리를 이용한 탐색 방법에 대해 알아보자.
01 "탐색이란?"
탐색이란? 데이터의 집합에서 원하는 조건을 만족하는 데이터를 찾는 작업이다.
탐색을 위한 대상을 레코드(record)라 하고,
이러한 레코드의 집합을 테이블(table)이라 한다.
하나의 레코드는 여러 개의 필드로 이루어지는데,
이 중에서 탐색의 기준이 되는 필드를 키(key) 또는 탐색키(search key)라고 한다.
결국 탐색은 테이블에서 원하는 키 또는 탐색키를 가진 레코드를 찾는 작업이다.
탐색에서 테이블을 구성하는 방법에 따라 효율이 달라진다.
가장 간단한 방법은 배열을 사용해 레코드를 저장하고 찾는 것이다.
성능을 더 높이고 싶다면 이진 탐색 트리나 해싱을 사용하여 찾는 것이다.
(해싱은 추가로 설명하도록 하겠다⭐)
테이블에 수정이 없는 경우 탐색 연산의 효율이 가장 중요하겠지만,
테이블에 레코드를 추가하거나 꺼내는 삽입과 삭제 연산이 일어난다면 탐색과 함께 삽입과 삭제 연산도 고려하여 종합적으로 효율적인 알고리즘을 선택해야한다.
02 "순차 탐색"
순차 탐색(sequential search) 또는 선형 탐색(linear search)은 일렬로 늘어선 자료(레코드) 중에서 원하는 킷값을 가진 레코드를 찾는 알고리즘이다.
테이블은 배열이나 연결 리스트로 구성될 수 있다.
순차 탐색은 테이블의 각 레코드를 처음부터 하나씩 순서대로 검사하여 원하는 레코드를 찾는다. 레코드가 정렬되어 있지 않아도 찾을 수 있다.
알고리즘 코드를 통해 구체적인 처리 과정을 살펴보자.
def sequential_search(A, key, low, high):
for i in range(low, high + 1): # i : low, low+1, ..., high
if A[i] == key: # 탐색 성공하면
return i # 인덱스 반환
return -1 # 실패하면 -1 반환리스트의 low부터 high까지 순서대로 비교하며 원하는 킷값을 발견하면 해당 레코드의 위치를 반환한다.
원하는 킷값이 없다면 -1을 반환한다.
순차 탐색의 시간 복잡도는 모든 레코드를 항상 탐색해야하므로 이다.
순차 탐색의 특징
- 탐색의 정의를 직접 사용하는 알고리즘으로 간단하고 규현하기 쉽다.
- 효율적이지는 않다. 하지만 탐색 성능은 최선의 경우 이고 최악이나 평균적인 경우 이다.
- 테이블이 정렬되어 있지 않다면 순차 탐색 이외에 별다른 대안이 없다.
순차 탐색 개선 방법
순차 탐색을 개선할 방법은 없을까?
레코드 중에서 자주 검색되는 것들을 가능한 한 앞에 두는 것이다. 이러한 방법을 자기 구성(self-organizing) 순차 탐색이라 한다.
탐색이 진행될 때마다 자주 사용되는 레코드를 앞쪽으로 옮기는 방법으로 리스트를 재구성하여 탐색의 효율을 끌어올리려는 것이다. 이런 리스트를 자기 구성 리스트라 한다.
리스트를 재구성 하는데에는 여러 방법들이 있다.
1) 맨 앞으로 보내기 (move to front)
가장 간단한 방법은 탐색에 성공한 레코드를 리스트의 맨 앞으로 보내는 방법이다.
배열 구조의 리스트에 이 방법을 적용하는 경우, 원하는 킷값을 맨 앞으로 옮기고 이것 이전의 모든 레코드를 한 칸씩 뒤로 밀어야한다.
연결 리스트에 이 방법을 적용하는 경우, 해당 킷값의 링크를 시작 노드와 연결하고 바로 앞 노드의 링크를 킷값 뒤의 노드로 연결하면 된다. 복잡하지만 훨씬 효율 적이다.
이 방법은 모든 상황에서 효율적인 것은 아니고, 한번 탐색된 레코드가 바로 이어서 다시 탐색될 가능성이 많은 응용에만 사용해야한다.
2) 교환하기 (transpose)
탐색된 레코드를 맨 앞이 아닌 바로 앞의 레코드와 교환하는 방법이다.
자주 탐색되는 레코드는 점진적으로 앞으로 이동하고, 그렇지 않은 레코드들은 뒤로 밀리는 효과가 있다.
교환하기 전략을 추가한 알고리즘을 살펴보자.
def sequential_search_transpose(A, key, low, high):
for i in range(low, high + 1):
if A[i] == key:
if i > low: # 맨 처음 요소가 아니면
A[i], A[low] = A[low], A[i] # 교환하기(transpose)
i = i - 1 # 한칸 앞으로 이동
return i # 탐색에 성공할 시 키 값의 인덱스 반환
return -1 # 실패시 -1 반환3) 이 외 방법
위 두 방법 이 외에도 레코드마다 탐색된 횟수를 별도의 공간에 각각 저장해 두고, 탐색된 횟수가 많은 순으로 테이블을 재구성하는 전략(frequency count method)을 사용할 수도 있다.
이 방법들 모두 '자주 탐색된 레코드가 앞으로도 더 자주 탐색될 가능성이 큰 응용의 상황'에만 적용되어야한다.
+) 순차 탐색 연결 리스트로 구현
def search(self, elem):
node = self.head
while node != None:
if node.data = elem:
return node
node = node.link
return None+) 순차 탐색 (연결 리스트): 맨 앞으로 보내기
def search_m2f(self, elem):
if self.isEmpty():
return None
if self.head.data == elem:
return self.head
before = self.head
while before.link != None:
if before.link.data == elem:
n = before.link
before.link = n.link
n.link = self.head
self.head = n
return n
before = before.link
return None03 "이진 탐색"
이진 탐색(binary search)은 테이블이 킷값을 기준으로 정렬되어 있다면 보다 효율적인 알고리즘이다.
한번 비교할 때마다 탐색 범위가 절반으로 줄어들기 때문에 '이진'이란 이름이 붙었다.
탐색 과정은 다음과 같다.
-
테이블의 중앙에 있는 레코드를 탐색 키와 비교한다.
이때, 만약 중앙 레코드의 킷값이 탐색 키와 같으면 성공한 것이고, 중앙 레코드의 위치(인덱스)를 반환하면 된다. () -
중앙 레코드가 탐색 키보다 크면 탐색키의 왼쪽에 있는 레코드들만 탐색하면 된다.
중앙 레코드가 탐색 키보다 작으면 탐색키의 오른쪽에 있는 레코드들만 탐색하면 된다.
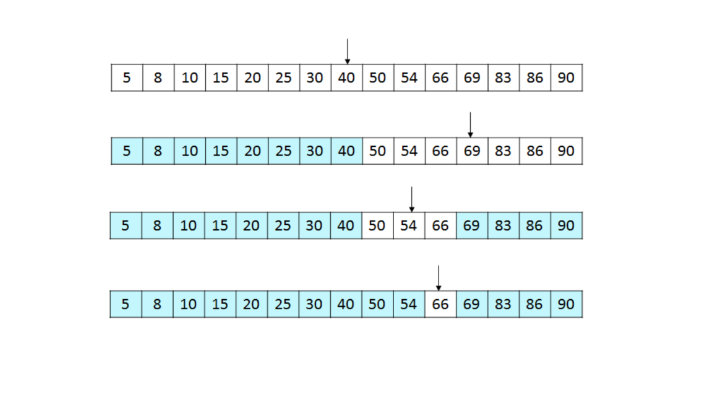
위 그림은 이진 탐색으로 66을 찾는 과정을 그림으로 나타낸 것이다.
하얀 부분이 검색해야 할 레코드인데 단계마다 검색해야 할 레코드의 수가 반으로 줄어드는 것을 알 수 있다.
그림에서는 탐색 키가 66인데 만약 탐색 키가 67이나 68이라면 검사 해볼 레코드가 없어지므로 -1을 반환하게 된다.
이제 이런 과정을 알고리즘으로 나타내 보자.
이진 탐색 알고리즘
이진 탐색을 알고리즘으로 표현하는 방법으로는 순환 구조를 사용하는 방법, 반복 구조를 사용하는 방법이 있다.
1. 순환 구조
def binary_search(A, key, low, high):
if (low <= high): # 검색해야 할 레코드가 있는 경우
middle = (low + high) // 2 # middle 계산
if key == A[middle]: # 탐색 성공 O(1)
return middle # 중앙 레코드의 인덱스 반환
elif (key < A[middle]): # 왼쪽 부분 리스트 탐색 (순환 호출)
return binary_search(A, key, low, middle - 1)
else: # 오른쪽 부분 리스트 탐색 (순환 호출)
return binary_search(A, key, middle + 1, high)
return -1 # 탐색 실패2. 반복 구조
def binary_search_iter(A, key, low, high):
while (low <= high): # 검색해야 할 레코드가 있는 경우
middle = (low + high) // 2 # middle 계산
if key == A[middle]: # 탐색 성공 O(1)
return middle # 중앙 레코
elif (key < A[middle]): # 왼쪽 부분 리스트 (low ~ middle-1) 탐색
high = middle - 1
else: # 오른쪽 부분 리스트 (middle+1 ~ high) 탐색
low = middle + 1
return -1 # 탐색 실패이진 탐색의 특징
이진 탐색의 최선의 경우는 정렬된 배열에서 중앙값이 탐색 키라면 로 가장 빠르게 탐색할 수 있고,
최악의 경우나 평균의 경우는 의 복잡도를 갖는 알고리즘이다.
정리하자면
- 의 매우 효율적인 탐색 방법이다.
- 반드시 배열이 정렬되어 있어야 사용 가능하다.
- 테이블이 한번 만들어지면 이후로 변경되지 않고 탐색 연산만 처리한다면 이진 탐색이 최고의 선택 중 하나다.
만약 테이블에 레코드를 삽입하거나 삭제하는 일이 빈번하게 일어나는 응용이라면
테이블이 배열구조이기 때문에 삽입할 때는 삽입할 위치 이후의 모든 레코드를 한 칸씩 뒤로 밀어야하고, 삭제할 때는 삭제한 위치 이후의 모든 레코드를 한 칸씩 앞으로 당겨야한다.
정렬된 테이블에 레코드를 삽입하기 위해서 n에 비례하는 시간인 이 소요된다.
따라서, 데이터의 삽입이나 삭제가 빈번한 응용에는 이진 탐색이 좋지 않다. 이런 응용에는 이진 탐색 트리가 더 좋다.
그렇다면 연결된 구조에서의 이진 탐색은 어떨까?
연결된 구조에서는 시작 노드와 마지막 노드를 알고 있더라도 중간 노드를 찾는 것이 쉽지 않기 때문에 주로 테이블이 배열 구조인 상황에서 이진 탐색을 사용한다.
보간 탐색
보간 탐색(interpolation search)란? 이진 탐색의 일종으로 탐색 키가 존재할 위치를 예측하여 탐색하는 방법이다.
기존 이진 탐색에서는 탐색 키를 항상 중앙에 있는 레코드로 선택한다.
보간 탐색에서는 탐색 위치를 결정할 때 탐색 키가 있는 곳에 좀 더 근접하도록 가중치를 주겠다는 것이 핵심이다.
따라서 탐색 범위의 가장자리(low, hig)에 있는 레코드의 킷값과 탐색 키의 비율을 고려하여 다음과 같이 탐색 위치를 계산한다.
👉 탐색위치
따라서 위를 알고리즘에 적용하면 이진 탐색 함수에서 middle 계산만 아래와 같이 바꾸면 된다.
middle = int(low + (high-low) * (key-A[low]) / (A[high]-A[low]))위치의 비율을 계산하기 때문에 실수를 사용하지만 마지막에 인덱스로 변경할 때에는 정수로 변환해야해서 int()로 변환해주었다.
많은 데이터가 비교적 균등하게 분포된 자료의 경우 훨씬 효율적으로 사용될 수 있다.
04 "이진 탐색 트리"
이진 탐색 트리(BST: Binary Search Tree)는 효율적인 탐색을 위한 이진 트리인데, '이진 탐색을 위한 트리'라고 이해해도 무방하다.
이진 탐색 트리가 필요한 이유는 이진 탐색에서 삽입과 삭제가 어렵다는 것을 보완하기 위해 나온 방법이다.
탐색의 성능은 유지하면서 삽입과 삭제도 효율적으로 처리하려고 하는 것이다.
- 이진 탐색 트리 조건
이진 탐색 트리는 '모든 노드가 왼쪽 자식 노드는 나보다 작고, 오른쪽 자식 노드는 나보다 크다.'라는 규칙을 따르는 이진 트리다.
그리고 킷값의 중복을 허용하지 않는다. (이는 이후 설명할 삽입에서 중요한 역할을 한다!)
아래 그림을 예시로 보자
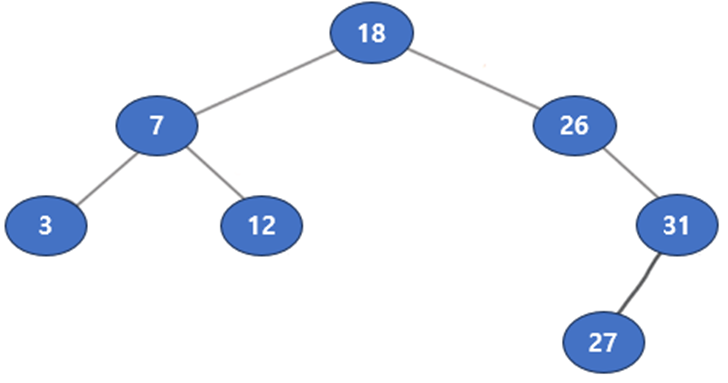
트리를 중위순회로 방문하면 오름차순으로 노드를 방문하게 된다. [3, 7, 12, 18, 26, 27, 31]
이진 탐색 트리는 어느 정도 정렬된 상태를 유지하고 있다 볼 수 있다.
이진 탐색 트리의 탐색 연산
이진 탐색 트리도 탐색이 목적이기 때문에 탐색 연산이 가장 중요하다.
key를 가진 노드를 찾는 과정을 알아보자.
-
12 찾기
루트인 18보다 작으므로 왼쪽 자식으로 이동 → 7보다 크므로 오른쪽 자식으로 이동 → 노드 값과 탐색 키와 동일 (탐색 성공 종료) -
32 찾기
루트인 18보다 크므로 오른쪽 자식으로 이동 → 26보다 크므로 오른쪽 자식으로 이동 → 31보다 크므로 오른쪽 자식으로 이동 → 자식이 없음. (탐색 실패 종료)
노드 클래스 BSTNode
이진 탐색 트리를 위한 노드는 일반적인 이진 트리 노드 BTNode와 비슷하게 데이터와 두 개의 링크를 갖도록 정의할 수 있지만, 데이터는 좀 세분하는 것이 편리하다.
즉, 탐색을 위한 키(key)와 나머지 데이터 부분(value)으로 나눈다.
# 코드 7.5: 이진 탐색 트리를 위한 노드 클래스
class BSTNode:
def __init__(self, key, value):
self.key = key # 키(key)
self.value = value # 값(value)
self.left = None
self.right = None탐색 알고리즘 1: 키를 이용한 탐색
탐색은 다음과 같이 순환 구조로 나타낼 수 있다.
# 코드 7.6: 이진 탐색 트리의 탐색 연산(순환 구조)
def search_bst(n, key):
if n == None:
return None
elif key == n.key:
return n # 탐색 성공
elif key < n.key:
return search_bst(n.left, key) # 왼쪽 서브트리에서 탐색
else:
return search_bst(n.right, key) # 오른쪽 서브트리에서 탐색이를 반복 구조로도 나타낼 수 있다.
# 코드 7.6.1: 이진 탐색 트리의 탐색 연산(반복 구조)
def search_bst_iter(n, key):
while n != None:
if key == n.key:
return n # 탐색 성공
elif key < n.key:
n = n.left # 왼쪽 서브트리에서 탐색
else:
n = n.right # 오른쪽 서브트리에서 탐색
return None 탐색 알고리즘 2: 값을 이용한 탐색
이진 탐색 트리는 킷값을 기준으로 정렬되어 있다.
트리의 모든 노드를 하나씩 검사하면 필드를 이용한 탐색도 가능하다.
최악의 경우 트리의 모든 노드를 검사해야 하므로 탐색 성능은 키를 이용한 탐색에 비해 떨어진다.
전위, 중위, 후위, 레벨 순회 등 순회는 모두 가능하나 전위순회를 이용해서 코드를 작성해보자.
# 코드 7.7: 이진 탐색 트리의 값을 이용한 탐색(전위순회)
def search_value_bst(n, value):
if n == None:
return None
elif value == n.value:
return n # 탐색 성공
res = search_value_bst(n.left, value)
if res is not None:
return res # 왼쪽 서브트리에서 탐색
else:
return search_value_bst(n.right, value) # 오른쪽 서브트리에서 탐색이진 탐색 트리의 삽입 연산
삽입을 위해서는 먼저 삽입할 노드의 키를 이용한 탐색 과정을 수행하고 탐색에 실패한 위치에 새로운 노드를 삽입하는 방식이다.
아래 그림에서 이진 트리에 새로운 노드 9를 추가한다고 생각해보자.
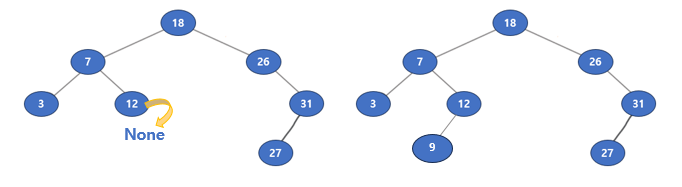
루트인 18보다는 작기 때문에 왼쪽 자식으로 내려가고,
7보다는 크기 때문에 오른쪽 자식으로 내려가고,
12보다 작기 때문에 왼쪽 자식으로 내려간다.
왼쪽 자식이 없기 때문에 탐색에 실패하고 해당 자리가 노드 9가 들어갈 자리다.
탐색에 성공하면 이진 트리에서는 중복을 허용하지 않기 때문에 노드를 새로 삽입하지 않는다.
삽입 연산도 순환으로 구현하는 것이 가장 자연스럽고 루트가 root인 트리에 새로운 노드 node를 삽입하는 연산을 구현할 것이다.
최종적으로 오게 될 노드를 반환해야한다.
# 코드 7.8: 이진 탐색 트리의 삽입 연산
def insert_bst(root, node):
if root == None: # 공백 노드에 도달하면, 이 위치에 삽입
return node # node를 반환
if node.key == root.key:
return root # 삽입 실패, root를 반환
# root의 서브 트리에 node 삽입
if node.key < root.key:
root.left = insert_bst(root.left, node)
else:
root.right = insert_bst(root.right, node)
return root이진 탐색 트리의 삭제 연산
노드를 삭제하는 것은 이진 탐색 트리에서 가장 복잡한 연산이다.
노드를 삭제한 후에도 이진 탐색 트리의 특성이 반드시 유지되어야 하기 때문이다.
이 연산은 삭제할 노드의 자식 수에 따라 3가지 경우로 구분된다.
Case 1: 단말 노드의 삭제
삭제할 노드가 자식이 없는 단말 노드라면 해당 노드만 삭제하면 되기 때문에 가장 간단하다.
알고리즘에서 실제로 변경되는 것은 부모의 링크 필드다.
Case 2: 자식이 하나인 노드의 삭제
삭제할 노드가 하나의 자식을 갖는다면 그 자식을 부모 노드에 연결해주면 된다.
예를 들면 아래 트리에서 68 노드를 삭제한다면
자식 노드인 99를 부모 노드로 옮기면 된다.
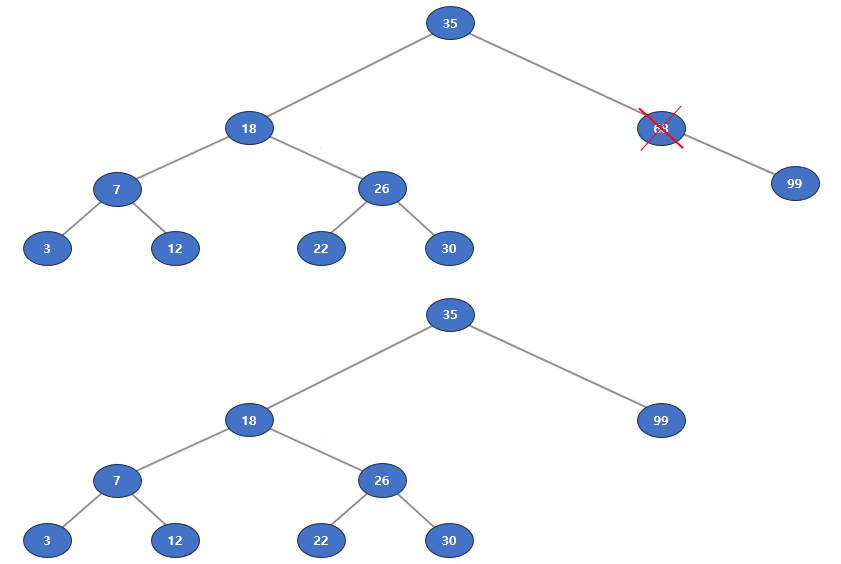
Case 3: 2개의 자식을 모두 갖는 노드의 삭제
2개의 자식을 모두 갖는 경우 자식 중 적절한 노드(후계자)를 찾고, 후계자의 데이터를 삭제할 노드에 복사한 다음, 실제로는 후계자를 삭제하는 것이다.
삭제할 노드와 킷값이 최대한 비슷한 노드가 좋을 것이다.
후계자 노드의 후보는 아래와 같다.
- 삭제할 노드의 왼쪽 서브 트리에서 가장 큰 노드
- 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 노드
예를 들어 노드 18을 삭제하면 노드 18의 왼쪽 서브트리에서 가장 큰 노드는 12, 오른쪽 서브트리에서 가장 작은 노드는 22이다.
이 둘이 관계는 이진 탐색 트리를 중위 순회했을 때, 삭제할 노드의 바로 앞과 뒤에 있는 노드다.
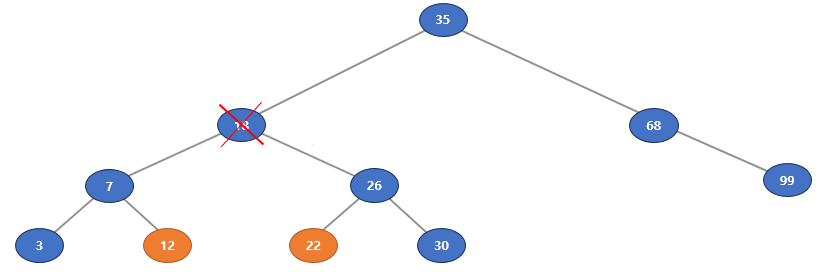
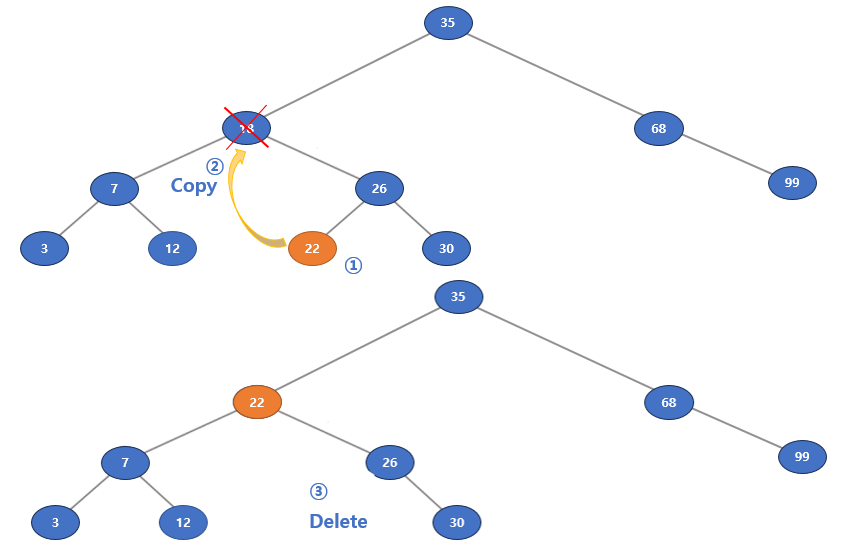
여기서 오른쪽 서브 트리의 가장 작은 노드 22를 후계자로 사용할 경우 다음과 순서로 삭제가 이루어진다.
① 삭제할 노드의 후계자를 찾는다. → 22
② 후계자(succ, 22)의 데이터 (키, 값)를 모두 삭제할 노드(root, 18)에 복사한다.
③ 후계자 노드를 삭제한다. 삭제할 노드의 오른쪽 서브트리(26)에서 후계자의 킷값을 가진 노드를 삭제한다.
삭제 연산은 순환 구조로 구현할 수 있다.
삽입 연산과 비슷하게 킷값에 따라 이진 탐색을 진행하고, 삭제할 노드를 찾으면 각 경우에 따라 삭제를 진행한다.
항상 삭제할 노드(root)를 대신할 노드가 반환되어야 하는 것을 명심하자!
# 코드 7.9: 이진 탐색 트리의 삭제 연산
def delete_bst(root, key):
if root == None:
return root
if key < root.key:
root.left = delete_bst(root.left, key)
elif key > root.key:
root.right = delete_bst(root.right, key)
# key가 루트의 키와 같으면 root를 삭제
else:
# Case 1 (단말 노드) or Case 2 (오른쪽 자식만 있는 경우)
if root.left == None:
return root.right
# Case 2 (왼쪽 자식만 있는 경우)
elif root.right == None:
return root.left
# Case 3 (두 자식이 모두 있는 경우)
succ = root.right
while succ.left != None:
succ = succ.left
root.key = succ.key
root.value = succ.value
root.right = delete_bst(root.right, succ.key)
return root순환호출 과정 분석
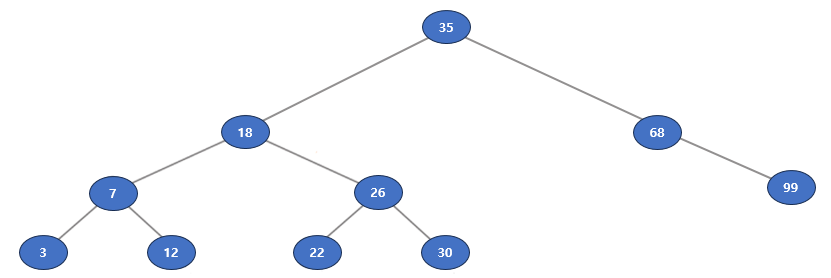
Case 1) 단말 노드 30 삭제
① delete_bst(35, 30) 6행
② delete_bst(18, 30) 8행
③ delete_bst(26, 30) 8행
④ delete_bst(30, 30) 13행
⑤ return None 14행
⑥ return 26 29행
⑦ return 18 29행
⑧ return 35 29행
Case 2) 자식이 하나인 노드 68 삭제
① delete_bst(35, 68) 8행
② delete_bst(68, 68) 13행
③ return 99 14행
④ return 35 29행
Case 3) 자식이 두 개인 노드 18 삭제
① delete_bst(35, 18) 6행
② delete_bst(18, 18) 27행
③ delete_bst(26, 22) 6행
④ delete_bst(22, 22) 13행
⑤ return None 14행
⑥ return 26 29행
⑦ return 22 29행
⑧ return 35 29행
이진 탐색 트리의 특징
- 트리의 높이를 h라 하면 이진 탐색 트리의 탐색, 삽입, 삭제 연산은 모두 h에 비례하는 시간이 소요된다.
- 최선의 경우 포화 이진 트리의 경우이며 이 때 로 가장 낮은 트리가 만들어지고 탐색과 삽입, 삭제 연산이 모두 에 처리된다.
즉, 이진 탐색과 탐색 성능은 같지만 삽입과 삭제 연산이 훨씬 효율적이다. - 최악의 경우 한쪽으로 치우치는 경사 트리인 경우 트리의 높이 h는 n과 같아진다. 따라서 n에 비례한 에 처리된다.
결국 이진 탐색 트리의 효율을 높이기 위해서는 트리가 좌우 균형을 유지하는게 좋다. 이를 위해 AVL 트리, 2-3 트리, 2-3-4 트리, B 트리, Red-Black 트리와 같은 다양한 균형 기법들이 제안되었다.
이진 탐색 트리의 테스트
지금까지 살펴본 내용을 이진 탐색 트리의 여러 연산을 테스트 해봄으로써 정리해보자.
트리를 화면에 출력하기 위한 print_tree() 함수는 전위순회를 이용해 구현했고,
탐색 연산의 결과를 출력하기 위한 print_node() 함수를 추가했다.
# 코드 7.10: 이진 탐색 트리의 테스트 프로그램
def print_node(msg, n): # 노드 출력 함수
print(msg, n if n != None else "탐색 실패")
def print_tree(msg, r):
print(msg, end="")
preorder(r)
print()
def preorder(n):
if n is not None:
print("{ ", end='')
print(n.value, end=' ')
preorder(n.left)
preorder(n.right)
print("} ", end='')
data = [(6, "여섯"), (8, "여덟"), (2, "둘"), (4, "넷"), (7, "일곱"), (5, "다섯"), (1, "하나"), (9, "아홉"), (3, "셋"), (0,"영")]
root = None
for i in range(0, len(data)):
root = insert_bst(root, BSTNode(data[i][0], data[i][1]))
print_tree("이진 탐색 트리(최초) : ", root)
# key를 이용한 탐색
n = search_bst(root, 3); print_node("srch 3 : ", n)
n = search_bst(root, 8); print_node("srch 8 : ", n)
n = search_bst(root, 0); print_node("srch 0 : ", n)
n = search_bst(root, 10); print_node("srch 10 : ", n)
# 값을 이용한 탐색
n = search_value_bst(root, "둘"); print_node("srch 둘 : ", n)
n = search_value_bst(root, "열"); print_node("srch 열 : ", n)
root = delete_bst(root, 7); print_tree("del 7 : ", root)
root = delete_bst(root, 8); print_tree("del 8 : ", root)
root = delete_bst(root, 2); print_tree("del 2 : ", root)
root = delete_bst(root, 6); print_tree("del 6 : ", root)
> 출력
이진 탐색 트리(최초) : { 여섯 { 둘 { 하나 { 영 } } { 넷 { 셋 } { 다섯 } } } { 여덟 { 일곱 } { 아홉 } } }
srch 3 : <__main__.BSTNode object at 0x7e0231e62560>
srch 8 : <__main__.BSTNode object at 0x7e0231e62440>
srch 0 : <__main__.BSTNode object at 0x7e0231e62740>
srch 10 : 탐색 실패
srch 둘 : <__main__.BSTNode object at 0x7e0231e60520>
srch 열 : 탐색 실패
del 7 : { 여섯 { 둘 { 하나 { 영 } } { 넷 { 셋 } { 다섯 } } } { 여덟 { 아홉 } } }
del 8 : { 여섯 { 둘 { 하나 { 영 } } { 넷 { 셋 } { 다섯 } } } { 아홉 } }
del 2 : { 여섯 { 셋 { 하나 { 영 } } { 넷 { 다섯 } } } { 아홉 } }
del 6 : { 아홉 { 셋 { 하나 { 영 } } { 넷 { 다섯 } } } } 후기
탐색에 대해 공부하다보니 MySQL이 많이 떠올랐다.
그리고 이진 탐색 트리는 정말 게임같이 재밌고 알고리즘 구현을 이해하는데 있어 재귀함수를 잘 이해하지 못하는 내가 좀 멍청하다고 느꼈다 ㅋㅋㅋ
그래도 PPT로 그림을 직접 그려가며 이해하려하니 도움이 많이 되었다.
정리하는데 그림 그리면서 하려니 오래 걸려서 이것도 일주일 만에 돌아왔다,,,
드디어 마지막으로 그래프만 남았다.
마지막까지 화이팅~!
(사실 학원 조교 면접이랑, 회사 지원서 작성 등 취준이랑 같이 하다보니 늦어졌다🥹)

