
Chapter: 그래프 (Graph)
그래프는 복잡하게 연결된 객체 사이의 관계를 표현할 수 있는 가장 자유로운 자료구조이다.
모든 선형 자료구조나 트리조차도 그래프로 나타낼 수 있어 그래프의 한 종류로 볼 수 있다.
01 "그래프란?"
그래프(graph)는 복잡하게 연결된 객체 사이의 관계를 효율적으로 표현할 수 있는 자료구조이다. 지하철 노선도, 전기 회로, 소셜 네트워킹 서비스(SNS)와 같은 다양한 분야에서 많은 객체가 서로 복잡하게 연결된 자료를 다루고 있다. 지금까지 공부한 선형 자료구조나 트리도 그래프로 표현할 수 있어 그래프는 가장 일반화된 자료구조이다.
그래프의 유래
레오하르트 오일러(Leonhard Euler) 수학자가 처음으로 '위치'라는 객체를 정점(vertex)으로, 위치 간의 관계인 '다리'는 간선(edge)으로 표현하여 그래프 문제로 변환하는 것에서 시작됐다.
오일러는 그래프에 존재하는 모든 간선을 한 번만 통과하면서 처음 정점으로 되돌아오는 경로를 오일러 경로(Eulerian tour)라 정의하고, 그래프의 모든 정점에 연결된 간선의 개수가 짝수일 때만 오일러 경로가 존재한다는 오일러의 정리를 증명하였다.
정점들 자체로는 큰 의미가 없지만, 이들을 간선으로 연결하면 '관계'가 만들어지고 그래프가 형성된다.
이때 정점은 객체를 의미하고, 간선은 이러한 객체 간의 관계를 나타내어, 정점 A와 B를 연결하는 간선은 (A, B)와 같이 정점의 쌍으로 표현한다.
그래프의 종류
그래프는 간선의 방향성과 정점 간의 연결 정도에 따라 여러 가지 그래프로 나뉜다.
-
무방향 그래프(undirected graph)
두 정점을 연결하는 간선에 방향성이 없는 그래프로 간선이 양방향으로 갈 수 있는 길일 경우이다.
따라서 두 정점 A와 B를 연결하는 간선(A, B)는(B, A)와 동일한 간선이다.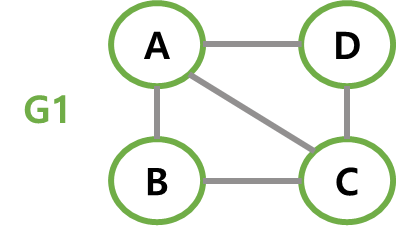

// 무방향 그래프 예시 V(G1) = {A, B, C, D} E(G1) = {(A,B), (A,C), (A,D), (B,C), (C,D)} V(G2) = {A, B, C} E(G2) = {(A,B), (A,C), (B,C)} -
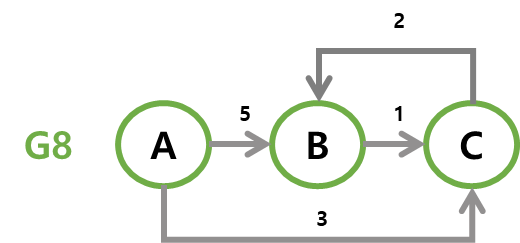
방향 그래프(directed graph)
간선에 방향이 있는 그래프로다이그래프(digraph)라고도 합니다. 간선이 한 방향으로만 갈 수 있는 길일 경우이다.
A에서 B로 가는 길은<A, B>로 표현하고,<A, B>와<B, A>는 서로 다른 간선이다.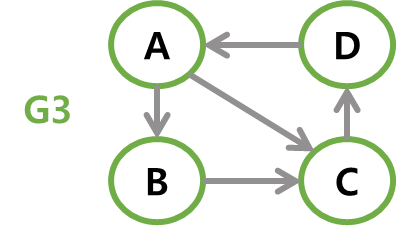
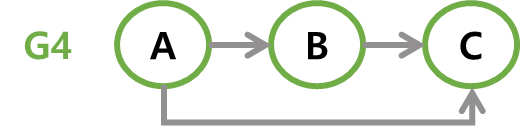
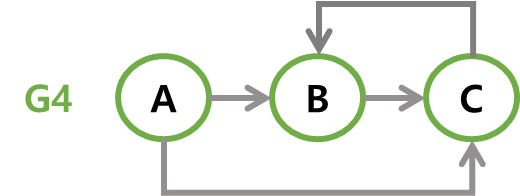
// 방향 그래프(다이그래프) 예시 V(G3) = {A, B, C, D} E(G3) = {<A,B>, <A,C>, <B,C>, <C,D>, <D,A>} V(G4) = {A, B, C} E(G4) = {<A,B>, <A,C>, <B,C>} -
완전 그래프(complete graph)
그래프의 모든 정점 사이에 간선이 존재하는 그래프를 말한다.
정점이 n개인 무방향 완전 그래프는 개의 간선을 갖고, 방향 그래프는 개의 간선을 갖는다.
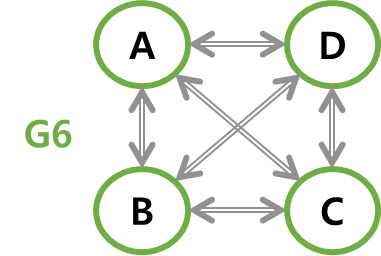
따라서 아래 G5는 무방향 완전 그래프이고, G6는 방향 완전 그래프다. (G5에서 하나의 간선이 G6에서 두 개의 간선에 해당.)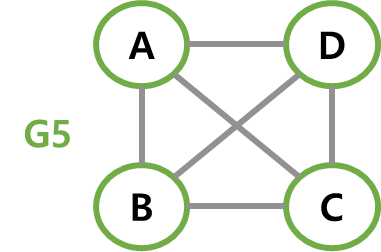
-
부분 그래프(subgraph)
원래의 그래프에서 정점이나 간선 일부만을 이용해 만든 그래프다.
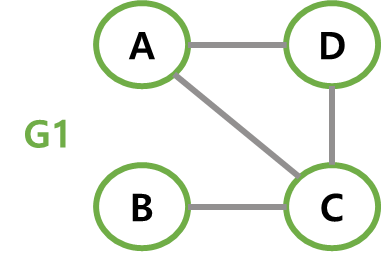
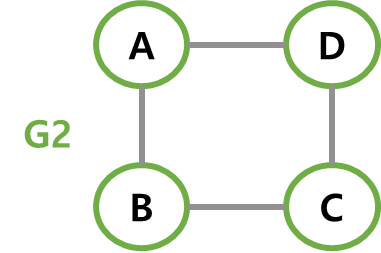
아래 그림에서 G1, G2, G3은 그래프 G의 부분 그래프다.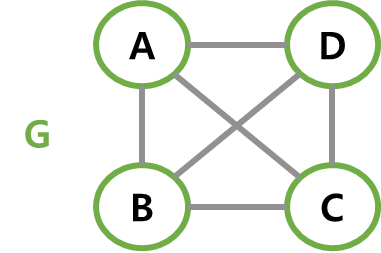
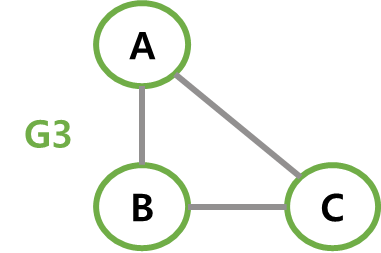
-
가중치 그래프(weighted graph)
간선에 가중치가 할당된 그래프를 가중치 그래프 또는 네트워크(network)라고 한다.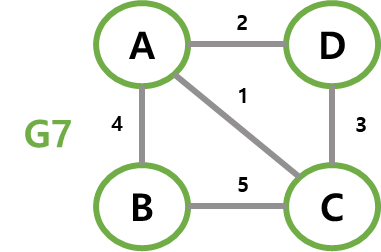
그래프의 용어
 |  |  |
|---|
-
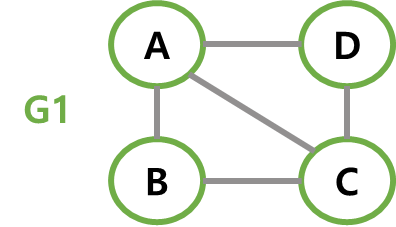
인접(adjacent)
: 간선으로 연결된 우 정점을 인접해 있다고 한다.
G1에서 A에 인접한 정점은 B, C, D다. -
정점의 차수(degree)
: 그 정점에 연결된 간선의 수를 말한다.
방향 그래프에서는 차수가 두 가지로 나뉘는데, 외부에서 오는 간선의 수를진입 차수(in-degree), 외부로 향하는 간선의 수를진출 차수(out-degree)라 한다.
G4에서 B의 차수는 3이고 이중 진입 차수가 2, 진출 차수가 1이다. -
경로(path)
: 간선을 따라갈 수 있는 길을 순서대로 나열한 것을 말한다.
그리고 경로를 구성하는 간선의 수를경로 길이(path length)라 한다.
G1에서 A~C의 경로는 A-B-C, A-D-C, A-C 등이 있고, A-B-C는 경로의 길이가 2, A-C는 경로의 길이가 1이다. -
단순 경로(simple path)
: 반복되는 간선이 없는 경로를 말한다.
G1에서 A-B-C는 단순 경로지만, B-A-C-A는 단순경로가 아니다. -
사이클(cycle)
: 시작 정점과 종료 정점이 같은 단순 경로를 말한다.
G1에서 B-A-C-B는 사이클이다. -
연결 그래프(connected graph)
: 모든 정점 사이에 경로가 존재하는 그래프를 말한다.
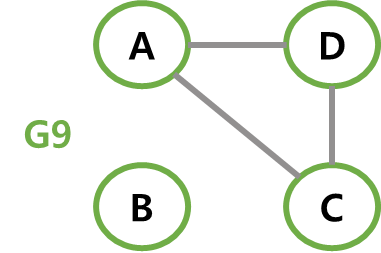
G1은 연결 그래프지만 G9는 연결 그래프가 아니다. -
트리(tree)
: 사이클을 가지지 않는 연결 그래프를 말한다.
02 "그래프의 표현"
그래프는 정점과 간선의 집합으로 구성되는데,
정점 집합은 리스트를 이용하면 쉽게 표현할 수 있다.
간선은 좀 복잡하다.
간선(u, v)는 정점 u와 v가 인접해 있다는 것을 말하는데, 그래프에서 정점들의 인접 관계를 어떻게 효율적으로 표현할 수 있을까?
인접 행렬과 인접 리스트를 사용할 수 있는데, 그래프의 특성과 필요한 연산에 따라 적절한 방법을 선택해야 한다.
인접 행렬을 이용한 표현
간선들의 집합을 표현하는 가장 간단한 방법은 2차원 배열을 이용하는 것이다.
이것을 인접 행렬(adjacency matrix)라 한다.
그래프의 정점 개수가 이라면 인접 행렬(2차원 배열)의 크기는 이고 행렬의 각 성분이 두 정점의 연결 관계를 나타낸다.
간선이 있으면 1, 없으면 0으로 나타냄으로써 아래 그림과 같이 무방향 그래프를 파이썬 2차원 배열로 나타낼 수 있다.
무방향 그래프에서는 인접 행렬이 항상 대칭행렬이다.
 |  |
|---|---|
| 무방향 그래프 | 파이썬 인접 행렬 표현 |
무방향 그래프는 배열의 상위 삼각이나 하위 삼각만 저장하여 메모리를 절약할 수도 있다.
위 그림의 그래프는 5개의 간선이 있으므로 인접 행렬에서 10개(5*2)의 원소가 1을 갖는다.
행렬의 대각선 성분은 모두 0으로 표현되고 이는 자신에서 출발해 자신으로 오는 간선이 없기 때문이다.
그래프에서 정점들 사이에는 순서가 없기 때문에 현재 인접행렬에서는 U, V, W, X, Y순으로 한거고 변경되면 행렬도 변경될 것이다.
인접리스트를 이용한 표현
각 정점이 인접한 정점 리스트를 갖도록 하여 간선들을 표현할 수 있는데 이러한 리스트를 인접 리스트(adjacency list)라고 한다.
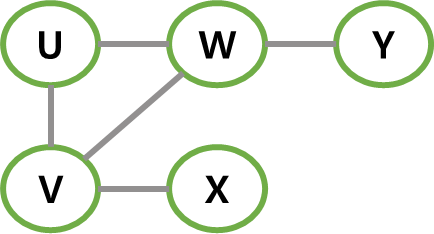
예를 들어, 아래 그림에서 정점 V는 U, W, X와 인접해 있고 따라서 길이가 3인 인접 리스트([0,2,3])로 표현할 수 있다.
그래프에서 정점 옆 숫자는 정점에 번호를 부여한 것이다.
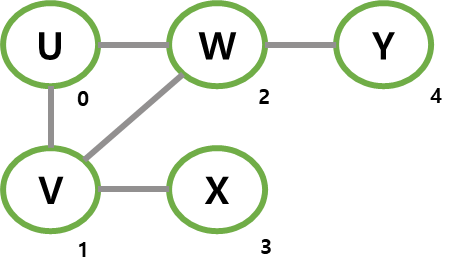 | 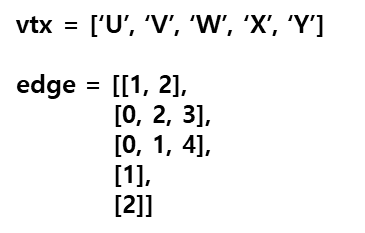 |
|---|---|
| 무방향 그래프 | 파이썬 인접 리스트 표현 |
이때 리스트로 연결 리스트를 사용할 수도 있고, 파이썬의 리스트와 같은 배열 구조를 사용할 수도 있다.
그래프의 '인접 리스트 표현'은 사실 개념적으로는 '인접 집합 표현'이라고 하는 것이 더 정확하다. 왜냐면 한 정점에 인접한 정점들 사이에는 순서가 없기 때문이다.
인접행렬 vs 인접리스트
단지 그래프를 표현하기 위해서라면 인접 행렬과 인접 리스트 어떤 것을 사용하더라도 괜찮다.
다만, 표현된 그래프로 어떤 작업을 하기 위해서라면 다르다.
정점이 개인 그래프를 표현하기 위한 메모리의 양은 인접 행렬의 경우 이므로 인접 리스트보다 약간 불리하다.
그래프에 간선 (u,v)가 있는지 검사하려면 행렬은 해당 성분을 바로 검사하면 되지만, 인접 리스트에서는 정점 u의 인접 리스트 v가 있는 하나씩 검사해야 하기 때문에 인접리스트가 불리하다.
이 외 다른 연산도 약간씩의 차이가 있지만 인접행렬과 인접리스트를 사용했을 때 약간의 장단점이 존재한다.
메모리의 사용량이 중요하거나 정점에 비해 간선이 별로 없는 희소 그래프(sparse graph)에서는 인접 리스트가,
정점끼리의 인접 여부를 빨리 알아내야 하거나 완전 그래프나 이와 유사한 조밀 그래프(dense graph)의 경우 인접 행렬이 더 좋은 선택일 것이다.
03 "그래프 순회"
그래프 순회는 하나의 정점에서 시작하여 그래프의 모든 정점을 한 번씩 방문하는 작업을 말한다.
실제로 많은 그래프 문제들이 단순히 정점들을 체계적으로 방문하는 것만으로 해결된다. ex) 전자회로 단자 간의 연결성 검사, 미로 탐색 문제
그래프의 정점들을 순회하는 체계적인 방법에는 깊이 우선 탐색과 너비 우선 탐색이 있다.
이 순회 방법은 이진 트리의 순회 방법과 비교해 볼 수 있다.
-
깊이 우선 탐색(DFS:Depth First Search)
: 시작 정점에서 한 방향으로 계속 가다가 더 이상 갈 수 없으면 가장 가까운 갈림길로 다시 돌아와 다른 방향을 다시 탐색한다. 이진트리의 전위순회와 비슷하다. -
너비 우선 탐색(BFS:Breadth First Search)
: 시작정점에서 가까운 정점을 먼저 방문하고 먼 정점을 나중에 방문한다. 이진 트리의 레벨순회와 비슷하다.
기억이 잘 안나는 분들을 위한 좌표 👉이진트리의 연산 - 전위순회, 레벨순회
깊이 우선 탐색(DFS:Depth First Search)
시작 정점에서 한 방향으로 갈 수 있는 곳까지 깊이 탐색을 진행하다가 더 이상 갈 곳이 없으면 가장 최근에 만났던 갈림길 정점으로 되돌아온다.
갈림길로 돌아와서는 가 보지 않은 다른 방향의 간선으로 탐색을 진행하고, 이 과정을 반복해 결국 모든 정점을 방문한다.
탐색과정에서 여러 갈림길을 만나지만 그중에서 가장 최근에 만났던 갈림길로 되돌아와야하므로, 이들을 후입선출 구조의 스택에 저장한다.
| - | 단계 | 깊이 우선 탐색 | 스택 |
|---|---|---|---|
| 0 | U에서 탐색을 시작. 맨 처음 스택에는 U만 있음. | 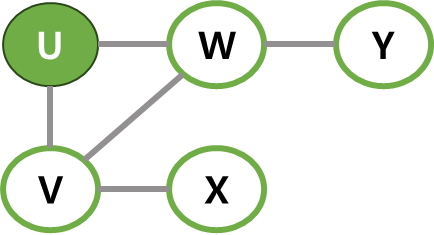 |  |
| 1 | 현재 정점은 스택 상단의 U. U의 인접 정점 중 하나인 V를 선택해 탐색을 진행. (우선 이 방향으로 가보기.) V를 스택에 넣고 이 정점이 현재 정점. | 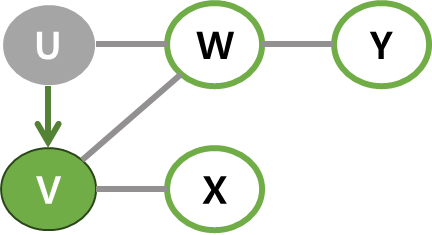 |  |
| 2 | V의 이웃 정점 중에서 아직 방문하지 않은 정점은 W와 X. 이 중 W를 선택해 탐색을 진행. W를 스택에 넣기. | 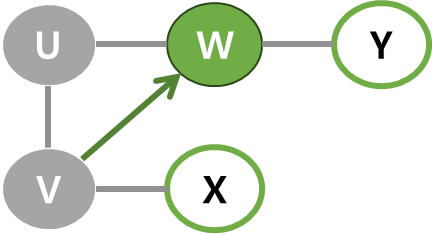 |  |
| 3 | W의 이웃 정점 중에서 아직 방문하지 않은 정점은 Y뿐. Y를 탐색 & Y를 스택에 넣기. | 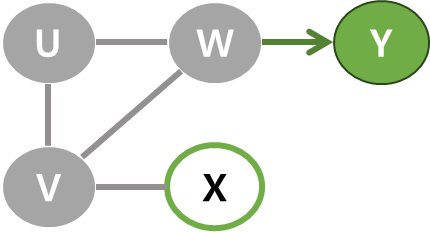 |  |
| 4 | Y의 이웃 정점 중에서는 방문하지 않은 정점이 없음. 이전으로 되돌아가기. 스택 상단의 Y를 삭제. | 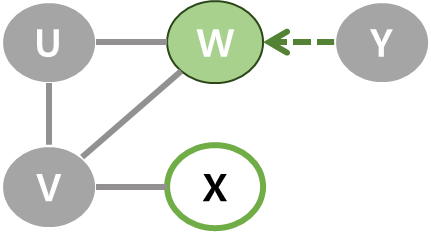 |  |
| 5 | 이제 스택 상단이 W. 가장 최근의 갈림길로 되돌아온 것. W도 방문하지 않은 이웃 정점이 없으므로 이전으로 되돌아가기. 스택 상단에서 W를 삭제. | 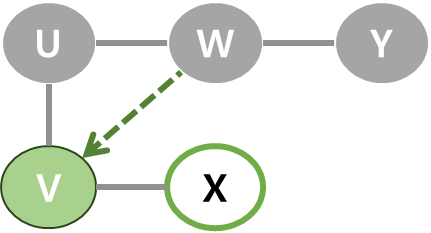 |  |
| 6 | 현재 정점이 V. V에서 남은 이웃 정점 X 탐색. X를 스택에 넣기. | 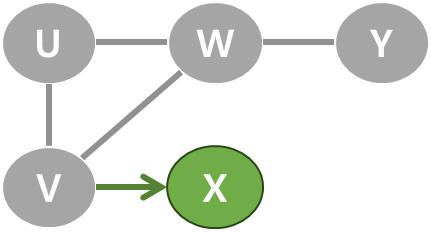 |  |
| 7 | X에 더 탐색할 이웃 정점이 없어 되돌아가기. V로 되돌아 갔다가 시작정점 U로 되돌아가기. U에서도 갈 수 있는 정점이 없으므로 탐색 종료. 정점의 방문 순서: U → V → W → Y → X | 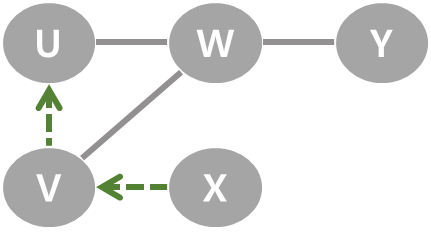 |  |
이제 이 깊이 우선 탐색을 구현해보자.
그래프는 인접 행렬로 표현한다.
정점 리스트 vtx와 인접 행렬 adj가 주어진다고 가정하고, 시작 정점은 s라고 한다.
각 정점의 방문 여부를 기록하기 visited 배열을 사용하는데, 맨 처음에는 모든 정점을 방문하지 않았으므로 False로 초기화 한다.
깊이 우선 탐색은 스택을 사용해 갈림길을 저장하는데, 시스템 스택을 이용하는 순환 호출을 이용하면 더 간결하게 구현할 수 있다.
# 코드 8.1: 깊이 우선 탐색(인접행렬 방식)
def DFS(vtx, adj, s, visited):
print(vix[s], end=' ')
visited[s] = True
for v in range(len(vtx)):
if adj[s][v] != 0:
if visited[v]==False:
DFS(vtx, adj, v, visited)
# 코드 8.2: 깊이 우선 탐색 테스트 프로그램
vtx = ['U', 'V', 'W', 'X', 'Y']
edge = [[0, 1, 1, 0, 0],
[1, 0, 1, 1, 0],
[1, 1, 0, 0, 1],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0]]
print('DFS(출발:U) : ', end='')
DFS(vtx, edge, 0, [False]*len(vtx))
print()
> 출력
DFS(출발:U) : U V W Y X 너비 우선 탐색(BFS:Breadth First Search)
가까운 정점부터 꼼꼼하게 살피고 먼 정점을 찾아가는 전략이다.
즉, 거리가 0인 시작 정점으로부터 거리가 1인 모든 정점을 방문하고, 거리가 2인 정점들, 거리가 3인 정점들 순으로 방문을 진행한다.
이것은 이진트리의 레벨 순회와 동작이 비슷하다.
너비 우선 탐색에서는 방문한 정점들을 차례대로 저장하고, 들어간 순서대로 꺼낼수 있는 큐를 사용한다.
BFS는 큐에서 정점을 꺼낼 때마다 아직 방문하지 않은 모든 인접 정점들을 방문하고 큐에 삽입한다. 이러한 탐색 과정은 큐가 공백 상태가 될 때까지 계속한다.
| - | 단계 | 너비 우선 탐색 | 큐 |
|---|---|---|---|
| 1 | 맨 처음에는 시작정점 U를 방문하고 큐에 넣기. | 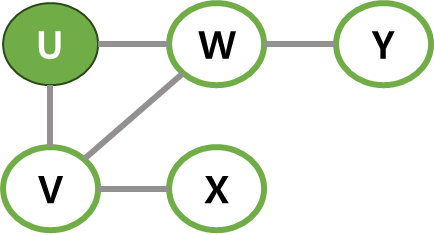 |  |
| 2 | 큐에서 U가 나오고, U의 이웃인 V와 W를 방문하고 큐에 넣기. | 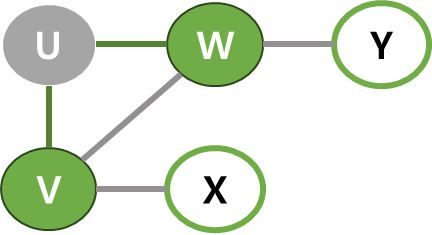 |  |
| 3 | 큐에서 V가 나오고 V의 이웃 중에서 아직 방문하지 않은 X를 큐에 넣기. | 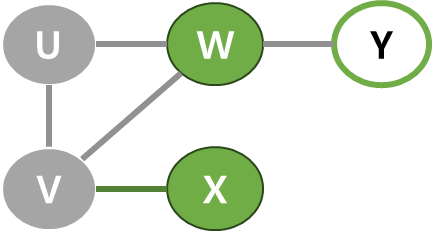 | 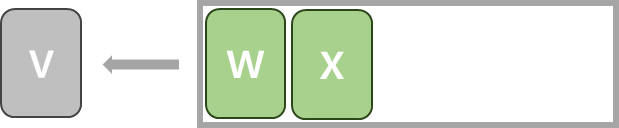 |
| 4 | 큐에서 W가 나오고 W의 이웃 중에서 아직 방문하지 않은 Y를 큐에 넣기. | 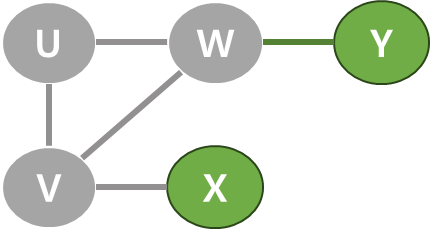 |  |
| 5 | 큐에서 X가 나오고 방문하지 않은 정점이 없음. | 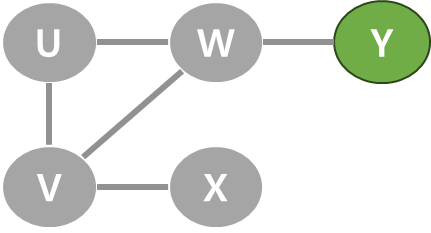 |  |
| 6 | 큐에서 Y가 나오고 방문하지 않은 정점이 없음. 큐가 공백상태가 되었기 때문에 탐색은 종료. 정점의 방문 순서: U → V → W → X → Y | 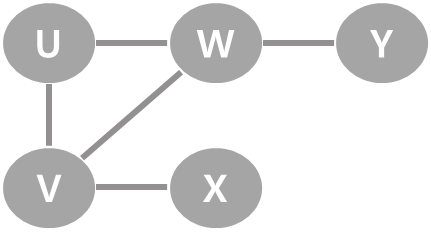 |  |
이제 BFS를 구현해보자.
그래프를 인접 리스트로 표현한다.
정점 리스트 vtx와 인접 리스트 aList가 주어진다고 가정하자.
시작 정점은 s고, 정점의 방문을 표시하는 배열 visited를 함수 내부에서 만들어 사용한다.
순환 호출을 이용한 DFS와 달리 BFS는 반복구조로 구현된다.
큐는 2장에서 구현한 원형큐 클래스나 파이썬의 queue나 collections 모듈을 사용할 수 있다.
이번에는 파이썬 queue모듈의 Queue 클래스를 사용한다.
# 코드 8.3: 너비 우선 탐색(인접리스트 방식)
from queue import Queue #queue 모듈의 Queue 사용
def BFS_AL(vtx, aList, s):
n = len(vtx) # 그래프의 정점 수
visited = [False]*n # 방문 확인을 위한 리스트
q = Queue()
q.put(s)
visited[s] = True
while not q.empty():
s = q.get()
print(vtx[s], end=' ')
for v in aList[s]:
if not visited[v]:
q.put(v)
visited[v] = True
# 코드 8.4: 너비 우선 탐색 테스트 프로그램
vtx = ['U', 'V', 'W', 'X', 'Y']
aList = [[1, 2],
[0, 2, 3],
[0, 1, 4],
[1],
[2]]
print('BFS(출발:U) : ', end='')
BFS_AL(vtx, aList, 0)
print()
> 출력
BFS(출발:U) : U V W X Y 만약 깊이 우선 탐색(DFS)에서 시작 정점이 U가 아니라 W였다면 정점의 방문 순서는 어떻게 될까?
W → U → V → X → Y가 될 것이다.
만약 너비 우선 탐색(BFS)에서 시작 정점이 U가 아니라 W였다면 정점의 방문 순서는 어떻게 될까?
W → U → V → Y → X가 될 것이다.
04 "신장 트리"
신장 트리(spanning tree)는 그래프 내 모든 정점을 포함하는 트리를 말한다.
즉, 그래프의 정점은 모두 포함하고, 간선은 일부만을 포함해 트리의 형태(사이클이 없어져야함)를 이루어야 한다. 하나의 그래프에는 여러 개의 신장 트리가 가능하다.
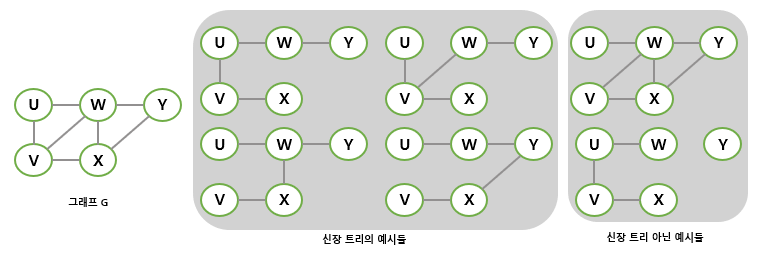
신장 트리도 트리의 일종이므로 당연히 모든 정점이 연결되어 있어야 한다. 또한, 트리이므로 사이클은 없어야 한다.
(신장 트리 아닌 예시들에서 확인할 수 있다.)
그래프의 정점 수가 이라면 신장 트리는 정확히 개의 간선으로 모든 정점을 연결해야한다.
신장 트리는 어떻게 구할 수 있을까?
DFS와 BFS를 이용해 구할 수 있다.
즉, 깊이 우선이나 너비 우선 탐색 도중에 사용된 간선들만 모으면 신장 트리가 만들어진다.
다음 코드는 코드 8.1을 수정하여 만든 신장트리 알고리즘이다.
# 코드 8.5: DFS를 이용한 신장트리(인접행렬 방식)
def ST_DFS(vtx, adj, s, visited):
visited[s] = True
for v in range(len(vtx)):
if adj[s][v] != 0:
if visited[v]==False:
print("(", vtx[s], vtx[v], ")", end=' ')
ST_DFS(vtx, adj, v, visited)
"""방문하지 않은 s의 이웃 정점 v가 있으면, 간선 (s,v)를 신장트리에 추가하고,
v를 시작으로 다시 깊이 우선 탐색 진행."""
# DFS를 이용한 신장트리 테스트 프로그램
vtx = ['U','V','W','X','Y']
edge= [[0, 1, 1, 0, 0],
[1, 0, 1, 1, 0],
[1, 1, 0, 0, 1],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0]]
print('ST_DFS_AM: ', end="")
ST_DFS(vtx, edge, 0, [False]*len(vtx))
print()
> 출력
ST_DFS_AM: ( U V ) ( V W ) ( W Y ) ( V X ) 너비 우선 탐색(시작 정점은 U)을 이용해 신장트리를 구해보자.
# BFS를 이용한 신장트리(인접리스트 방식)
from queue import Queue #queue 모듈의 Queue 사용
def ST_BFS(vtx, aList, s):
n = len(vtx) # 그래프의 정점 수
visited = [False]*n # 방문 확인을 위한 리스트
q = Queue()
q.put(s)
visited[s] = True
while not q.empty():
s = q.get()
for v in aList[s]:
if not visited[v]:
print("(", vtx[s], vtx[v], ")", end=' ')
q.put(v)
visited[v] = True
# BFS를 이용한 신장트리 테스트 프로그램
vtx = ['U', 'V', 'W', 'X', 'Y']
aList = [[1, 2],
[0, 2, 3],
[0, 1, 4],
[1],
[2]]
print('ST_BFS_AM: ', end="")
ST_BFS(vtx, aList, 0)
print()
> 출력
ST_BFS_AM: ( U V ) ( U W ) ( V X ) ( W Y ) 05 "최소 비용 신장 트리"
신장 트리는 위에서 배웠듯 그래프 내의 모든 정점을 포함하는 트리다.
이번엔 좀 특별한 트리를 배우려고 한다.
- 그래프의 모든 정점은 연결되어야 하고,
- 연결에 필요한 간선의 가중치 합(비용)이 최소가 되어야하는
최소 비용 신장 트리는 무엇일까?
만약 연결 방법 중에 사이클이 있으면 어떻게 될까?
사이클은 두 사이트를 연결하는 두 가지 경로를 제공하므로 비용 측면에서 절대 손해다.
이 문제의 해답은 주어진 그래프의 신장 트리 중에서 하나가 된다.
최소 신장 트리(MST:Mimimum Spanning Tree) 또는 최소 비용 신장 트리는 이처럼 가중치 그래프의 여러 신장 트리 중에서 간선의 가중치 합이 최소인 것을 말한다.
MST의 응용분야는 다음과 같이 다양하다.
- 통신망: 모든 사이트가 연결되도록 하면서 비용을 최소화하는 문제
- 도로망: 도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제
- 배관 작업: 파이프를 모두 연결하면서 파이프의 길이를 최소화하는 문제
- 전기 회로: 단자들을 모두 연결하면서 전선의 길이를 최소화하는 문제
최소 신장 트리를 구하는 방법에는 Kruskal과 Prim(프림)의 알고리즘이 있다.
우리는 Prim(프림)의 알고리즘에 대해 공부해보자.
프림 알고리즘
프림(Prim)은 하나의 정점에서부터 시작하여 최소 신장 트리(MST)를 단계적으로 확장해나가는 방법을 사용한다.
처음에는 MST에 시작정점만 포함되고, 다음부터 현재까지 만들어지 MST에 인접한 정점 중에서 간선의 가중치가 가장 작은(최소 간선) 정점을 선택하여 MST를 확장한다.
그리고 이 과정은 MST에 모든 정점이 삽입될 때까지 계속된다.
자연어로 기술한 알고리즘은 다음과 같다.
# 코드 8.6: 프림의 최소 신장 트리 알고리즘(자연어)
Prim()
그래프에서 시작정점을 선택하여 초기 트리(MST)를 만든다.
MST와 인접한 정점 중 간선의 가중치가 가장 작은 정점 v를 선택한다.
v와 이때의 간선을 MST에 추가한다.
아직 모든 정점이 삽입되지 않았으면 처음단계로 돌아가 순서를 반복한다.여기서 'MST에 인접한 정점 중에서 간선의 가중치가 가장 작은 정점을 선택한다.'라는 것이 뭔가 애매하다.
정점들의 상태를 저장할 배열을 두 개 사용할 것이다. 배열의 크기는 정점 수와 같다.
-
selected[]
: 정점이 MST에 포함되어있는지를 기록한다.
selected[v]가 True면 v가 MST에 포함된 것이다.
맨 처음에는 MST가 공백 트리이므로 배열의 모든 요소가 False가 되고 단계마다 선택되는 정점이 True로 변경된다. -
dist[]
: 현재까지 구성된 MST와 정점 사이의 최단 거리를 저장한다.
처음에는 시작정점의 값만 0이고 나머지는 모두 무한대(∞)다.
새로운 정점 u가 MST에 추가되면 u에 인접한 정점 v의 최단 거리 dist[v]가 더 짧아질 수 있다.
만약, 즉, 간선 (u,v)의 가중치가 기존의 dist[v]보다 적으면 dist[v]를 (u,v)의 가중치로 변경하는 것이다.
이렇게 하면 'MST에 인접한 정점 중에서 간선의 가중치가 가장 작은 정점을 선택한다.'을 확실하게 처리할 수 있다.
아직 선택되지 않은(selected가 False인) 정점 중에서 dist가 최소인 것을 찾으면 된다.
아래 예시를 통해 알고리즘 동작 단계를 확인해보자.
| - | 단계 | 배열 | 그래프 | 최소 신장 트리(MST) |
|---|---|---|---|---|
| 0 | 맨 처음에 MST는 공백 트리. (selected 모두 False) dist[]는 시작 정점 A만 0이고 나머지 ∞로 초기화. | 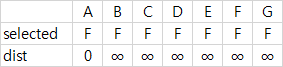 | 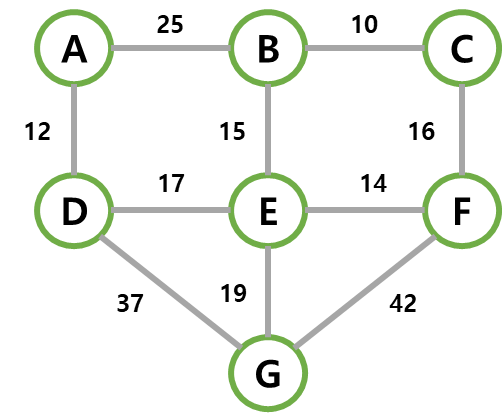 | |
| 1 | dist가 최소인 A를 MST에 넣는다.(selected 갱신) 이제 A의 인접 정점들의 dist를 갱신해야한다. 만약, A와 인접 정점 사이의 간선의 가중치가 기존 dist보다 작다면, 가중치를 갱신해야 한다. B와 D가 25, 12로 변경된다. | 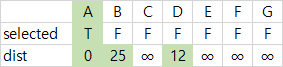 | 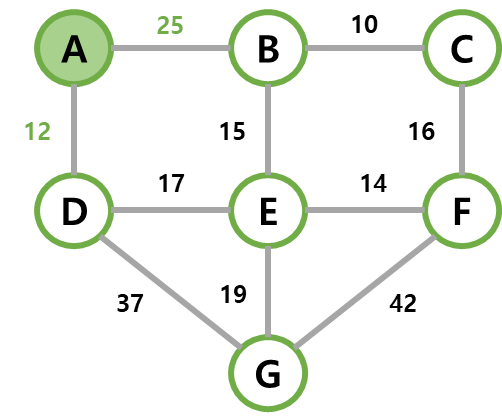 |  |
| 2 | dist가 최소인 D를 선택하고, 정점 D와 간선(A,D)를 MST에 넣는다. E와 G가 아직 선택되지 않은 인접 정점이고, 해당 dist를 17과 37로 갱신한다. | 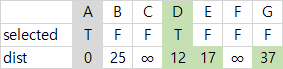 | 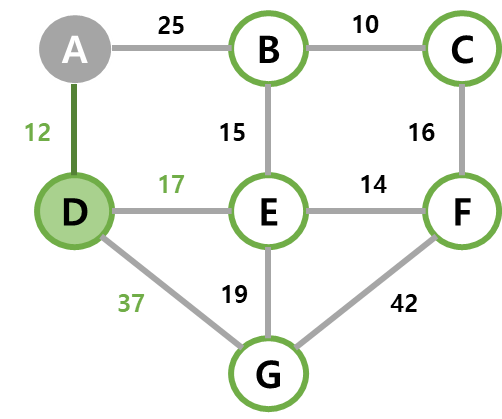 |  |
| 3 | dist가 최소인 E가 선택되고, E와 간선 (D, E)를 MST에 넣는다. B, F, G가 아직 선택되지 않은 인접 정점이라 기존 dist와 비교해 이들을 각각 15, 14, 19로 갱신해준다. | 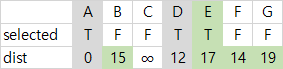 | 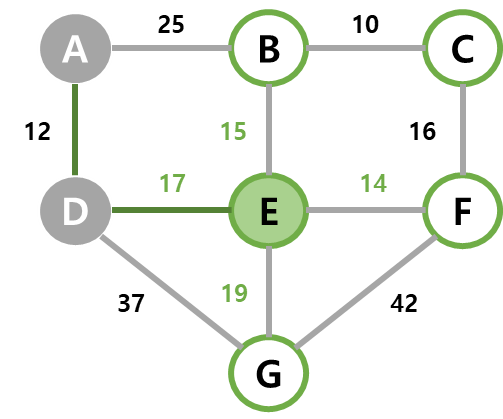 | 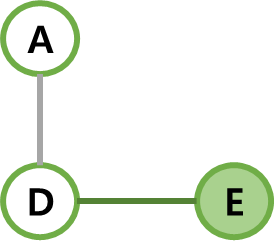 |
| 4 | dist가 최소인 F가 선택되고, F와 간선 (E, F)를 MST에 넣는다. C, G가 아직 선택되지 않은 인접 정점이라 기존 dist와 비교해 C를 16으로 갱신해준다. | 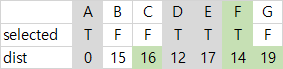 | 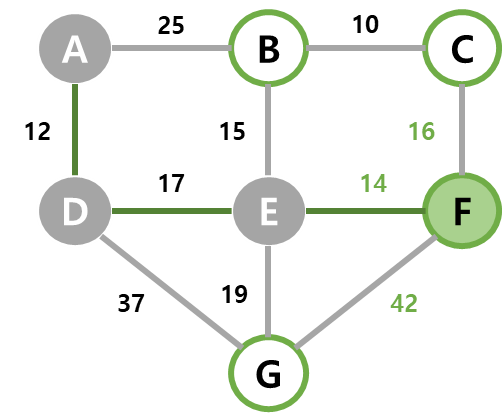 |  |
| 5 | dist가 최소인 B가 선택되고, B와 간선 (B,E)를 MST에 넣는다. C가 인접 정점인데 기존 dist보다 (B, C)의 가중치가 작아 C를 10으로 갱신한다. | 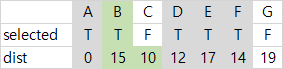 | 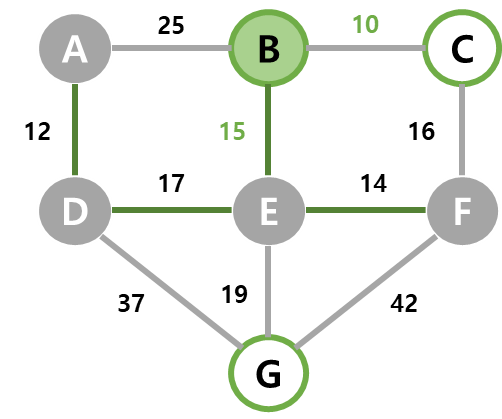 | 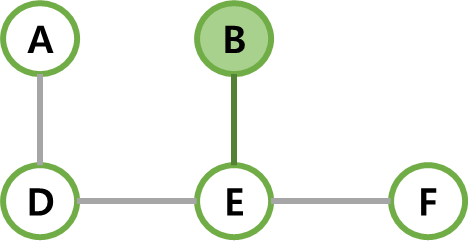 |
| 6 | dist가 최소인 C가 선택되고, C와 간선 (B, C)를 MST에 넣는다. 선택되지 않은 인접 정점이 없다. | 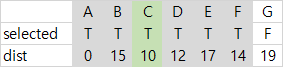 | 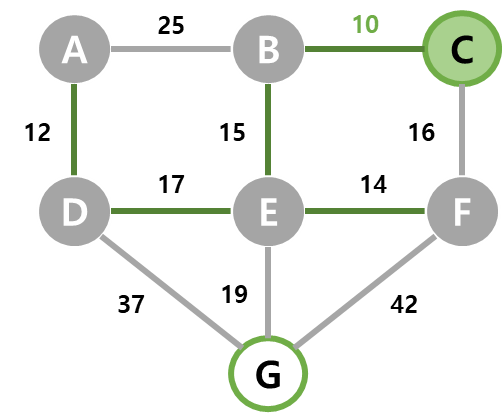 | 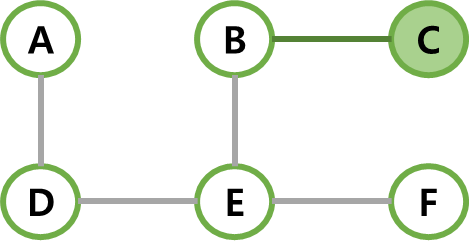 |
| 7 | 마지막으로 선택되지 않은 G정점을 선택하고, G를 간선 (E, G)와 함께 MST에 넣는다. MST가 완성되었다. |  | 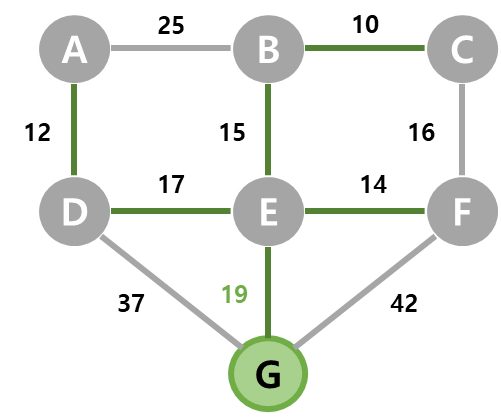 | 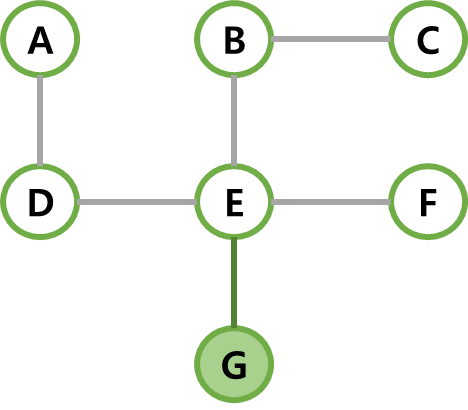 |
프림 알고리즘의 구현
이제 프림 알고리즘의 단계를 이해했으니 파이썬으로 알고리즘을 구현할 수 있다.
먼저 MST에 포함되지 않은 정점 중에서 dist가 최소인 것을 탐욕적으로 찾아 인덱스를 반환하는 함수는 다음과 같다.
(탐욕적 기법은 아래 추가로 내용을 다룰 예정이다.)
# 코드 8.7: MST에 포함되지 않은 최소 dist의 정점 찾기
INF = 999
def getMinVertex(dist, selected):
minv = 0
mindist = INF
for v in range(len(dist)):
if selected[v]==False and dist[v] < mindist:
mindist = dist[v]
minv = v
return minv
# 코드 8.8:프림의 최소 신장 트리 알고리즘
def MSTPrim(vertex, adj):
n = len(vertex)
dist = [INF]*n
selected = [False]*n
dist[0] = 0
for i in range(n): # n개의 정점을 MST에 추가하면 종료.
u = getMinVertex(dist, selected)
selected[u] = True
print(vertex[u], end=' ')
for v in range(n):
# 간선 (u, v)가 있고, v가 MST에 없다면
if adj[u][v] != 0 and not selected[v]:
if adj[u][v] < dist[v]: # (u, v)가 dist[v]보다 작으면
dist[v] = adj[u][v] # dist[v] 갱신
print(': ', dist) # 중간 결과 출력
print()
# Prim의 MST 테스트 프로그램
vertex = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
weight = [ [0, 25, INF, 12, INF, INF, INF],
[25, 0, 10, INF, 15, INF, INF],
[INF, 10, 0, INF, INF, 16, INF],
[12, INF, INF, 0, 17, INF, 37],
[INF, 15, INF, 17, 0, 14, 19],
[INF, INF, 16, INF, 14, 0, 42],
[INF, INF, INF, 37, 19, 42, 0]]
print("MST By Prim's Algorithm")
MSTPrim(vertex, weight)
> 출력
MST By Prim's Algorithm
A : [0, 25, 999, 12, 999, 999, 999]
D : [0, 25, 999, 12, 17, 999, 37]
E : [0, 15, 999, 12, 17, 14, 19]
F : [0, 15, 16, 12, 17, 14, 19]
B : [0, 15, 10, 12, 17, 14, 19]
C : [0, 15, 10, 12, 17, 14, 19]
G : [0, 15, 10, 12, 17, 14, 19]여기서 무한대는 999로 표현되었다.
프림 알고리즘은 얼마나 빠를까?
첫 for문인 외부 루프에서 정점의 수 n만큼 반복된다.
내부에서는 getMinVertex() 함수에 반복문이 있는데, 역시 n번 반복한다.
또 for문이 하나 더 내부 루프로 있으므로 이때도 n번 반복한다.
따라서 이 알고리즘은 외부와 내부 루프의 반복 횟수의 곱에 비례하는 연산이 필요할 것이고, 시간 복잡도는 가 된다.
+) 탐욕적 기법(greedy method)⭐
탐욕적 기법(greedy method)는 단순하고 직관적인 방법으로 모든 경우를 고려해 보고 가장 좋은 답을 찾는 것이 아니라 어떤 결정을 해야 할 때마다 "그 순간에 최적"이라고 생각되는 것을 선택하는 방법이다. "근시안적"인 알고리즘이라 할 수 있다.
순간에 최적이라고 판단했던 선택들을 모아 만든 최종적인 답이 '궁극적으로 최적'인 최적해가 될까? 항상 그렇진 않다.
따라서 탐욕적 기법이 사용될 수 있는 경우는 다음과 같이 두 가지로 제한된다.
- 최소 비용 신장 트리를 위한 프림 알고리즘, 최단 경로 거리를 구하는 다익스트라 알고리즘 등
- 시간이나 공간적인 제약으로 최적해가 현실적으로 불가능한 경우.(분기 한정 기법에서 좋은 한계값을 구할 때)
거스름돈 동전 최소화
액면가가 서로 다른 m 가지의 동전 이 있다.
거스름돈으로 V원을 동전으로만 돌려주어야 한다면 최소 몇 개의 동전이 필요한지를 구하세요.
단, 모든 동전은 무한히 사용할 수 있고, 액수가 큰 것부터 내림차순으로 순서대로 정렬되어 있다.
우리나라에는 {500원, 100원, 50원, 10원, 5원, 1원}의 6가지 동전이 사용되고 있다.
이 동전들로 몇 가지 거스름돈을 최소 동전으로 만들어보자.
- 거스름돈 620원: 500원 + 100원 + 10원×2 → 동전 4개
- 거스름돈 345원: 100원×3 + 10원×4 + 5원 → 동전 8개
- 거스름돈 572원: 500원 + 50원 + 10원×2 + 1원×2 → 동전 6개
액면가가 가장 높은 동전부터 탐욕적으로 최대한 사용하면서 거스름돈을 맞추면 어렵지 않게 동전 개수를 최소로 만들 수 있다.
하지만 만약 60원이라는 동전이 새로 생기게 된다면 620원의 경우 500원 + 60원×2 로 동전 3개만으로도 최소 동전을 만들 수 있기 때문에 탐욕적 기법이 항상 최적해를 구하진 않는다.
다만, 다음과 같은 동전 체계를 갖는다면 탐욕적 기법이 항상 최적해를 구하게 된다.
동전의 액면가 중에서 어떤 두 개를 고르더라도 큰 액면가를 작은 액면가로 나누어 떨어지는 동전 체계를 갖는다면 최적해를 보장한다. 작은 액면가를 여러 개 모으면 반드시 큰 액변가를 만들 수 있기 때문이다.
우리나라 동전이나 지폐의 단위는 이런 방법을 유지하기 때문에 이런 쳬게에서는 탐욕적 알고리즘이 항상 최적해를 보장한다.
분할 가능한 배낭 채우기
이 문제에 대한 두 가지 '탐욕'을 생각해 보자.
- 탐욕 1: 무게와 상관없이 가장 비싼 물건부터 넣는 방법.
- 탐욕 2: 단위 무게당 가격이 가장 높은 물건부터 넣는 방법.
1. 배낭 채우기 문제
배낭 채우기 문제는 위 두 가지 경우 모두 탐욕적 기법으로 최적해를 구하지 못한다.
최적해가 아닌 상황을 예시를 통해 알아보자.
세 개의 물건 A=(12kg, 120만원), B=(10kg, 80만원), C=(8kg, 60만원)이 있고 배낭의 용량이 18kg다.
최적해는 B와 C를 넣는 경우고 최대 가치는 140만원이다.
- 탐욕 1: 가장 비싼 물건은 A다. 따라서 A를 넣게 되면 B나 C를 넣을 용량이 안되기 때문에 배낭 가치는 120만원이고 최적해(140만원)보다 적다.
- 탐욕 2: 단위 무게당 가장 비싼 물건도 A다. 따라서 탐욕 1과 같이 최적해가 아니다.
하지만 이 문제를 약간 변형하면 최적해를 구할 수 있다.
2. 분할 가능한 배낭 채우기 문제
만약 물건들이 소분 가능해 일부분만 배낭에 넣을 수 있다면 어떨까? 이를 분할 가능한 배낭 채우기(Fractional Knapsack)문제라고 한다.
각각 무게가 이고 가치가 인 개의 물건이 있고, 이것을 배낭에 넣으려고 한다.
배낭에는 용량(최대 무게) 까지만 넣을 수 있다.
물건들의 가치의 합이 최대가 되도록 배낭을 채우고, 이 때 배나의 최대 가치를 구해보자.
단, 물건들은 나누어 일부분만 넣을 수도 있다.
이 문제에서는 배낭 채우기 문제와 달리 항상 배낭을 최대 용량으로 채울 수 있다.
파이썬 알고리즘으로 이 문제를 해결해 보자.
# 분할 가능한 배낭 채우기(탐욕적 기법)
def KnapSackFrac(wgt, val, W):
bestVal = 0 # 최대가치
for i in range(len(wgt)): # 단가가 높은 물건부터 처리
if W == 0: # 용량이 다 찼으면 채우기 종료
break
if W >= wgt[i]:
W -= wgt[i]
bestVal += val[i]
else:
fraction = W / wgt[i]
bestVal += val[i] * fraction
break
return bestVal # 최대 가치 반환
# 테스트 프로그램
weight = [12, 10, 8] # (정렬됨)
value = [120, 80, 60] # (정렬됨)
W = 18
print("Fractional Knapsack(18):", KnapSackFrac(weight, value, W))
> 출력
Fractional Knapsack(18): 168.0이 알고리즘은 넣을 수 있는 모든 공간을 항상 무게당 가격이 가장 높은 것부터 채우기 때문에 최적해를 확실히 보장한다.
알고리즘의 복잡도는 이다. 반복문이 하나 밖에 없기 때문이다.
후기
드디어 파이썬으로 배우는 자료구조 책도 완료했다!
부트 캠프 마지막쯤 부터 시작해서 이렇게 오래 걸리게 될 줄 몰랐다.😢
특히 이번 chapter에서는 그래프가 많아서 일일이 그리느라 더 오래걸렸던거 같다.😂
9월 초반을 마이다스 아이티 온라인 인턴십에 쏟아붓느라, 추석 연휴를 즐기느라 3주 동안은 코딩을 못했었다. 이 인턴십 관련해서 후기도 조만간 올릴 예정이다.😉
'열혈 C언어' 완독과 '자료구조와 알고리즘 with 파이썬' 완독을 했으니,
이제 '열혈 자료구조'를 통해 C언어로 자료구조를 알아보려한다.
왜이렇게까지 하나 싶겠지만,,, 재밌으니깐😎 새로운 개념이나 배움은 언제든 재밌다🤗💗
그럼 모두 keep coding~!

