PMI 값과 co-occurrence 행렬분해를 통해 word embedding을 수행하는 Swivel을 소개하는 논문입니다.
[Abstract]
해당 논문에서는 feature co-occurence 행렬로부터 저차원의 feature embedding을 만드는 방법인 Swivel(Submatrix-wise Vector Embedding Learner)를 소개합니다. Swivel은 stochastic gradient descent를 활용하여 PMI 행렬 분해를 근사합니다. Swivel은 piecewise loss를 사용하여 co-occurence가 존재하지 않는 경우를 처리하여 행렬의 모든 정보를 활용합니다. 이는 행렬의 크기에 비례하여 계산량을 필요로하지만 수백만의 예측값을 한번에 계산하기 위하여 수천개의 row와 column을 다루기위해 vectorized multiplication을 사용합니다. 더 나아가 Swivel을 통해 여러개의 node를 활용하여 병렬처리를 수행하기위해 행렬을 shard에 나눕니다.
1. Introduction
단어를 dense vector representation으로 표현하는 것은 다양한 자연어처리 작업에서 효율적이라는 것이 밝혀졌습니다. 다양한 연구들에서 stochastic gradient descent를 활용하여 word vector를 만드는 노력을 하고 있습니다. 이런 모델들은 2가지로 분류할 수 있습니다.
- matrix factorization -> count 기반
- sampling from a sliding window -> predict 기반
해당 논문에서는 co-occurence 행렬로부터 낮은 차원의 feature embedding을 만드는 count-based 방법인 Swivel을 소개합니다. Swivel은 궁극적으로 PMI(point-wise mutual information)을 재구성하는 embedding을 얻기위해 stochastic gradient descent를 사용하여 가중근사행렬분해(weighted approximate matrix factorization)을 수행합니다. Swivel은 또한 co-occurence의 등장여부의 차이를 두기위해 piecewise loss function을 사용합니다.
Swivel은 분산처리 환경에서 동작합니다. Co-occurence 행렬은 작은 크기의 sub-matrix로 분해되어 sharded됩니다. 이는 곧 수백만의 PMI값을 빠르게 예측하기 위해 vectorized matirx multiplication을 사용하는 여러개의 worker로 나누어집니다.
2. Related Work
Skipgram Negative Sampling(SGNS)와 GloVe는 word embedding 방법들 중 큰 주목을 받고 있는 대표적인 방법들입니다. 두 방법 모두 기존 언어의 co-occurence 통계량의 distributional 구조를 압축하여 기존 space의 특성을 유지한 채로 compact representaion(=dense representation)을 얻어냅니다. Embedding의 성능은 2가지 방법을 통해 평가됩니다.
- 유사한 문맥의 단어들은 유사한 embedding 공간에 위치해야 한다.
- Vector 공간에서 word embedding vector들의 연산을 통해 의미를 반영할 수 있다. = Analogical task
Skipgram Negative Sampling(SGNS) 은 text의 말뭉치에서 sliding을 통해 word embedding을 만듭니다. Window의 중심단어는 해당 단어 중심의 문맥 단어를 예측하며 학습됩니다. 해당 학습은 아래와 같은 방법으로 이루어집니다.
- 중심단어와 문맥단어로 sampling된 단어들의(positive sampling) embedding vector를 내적한 값을 최대로 만든다.
- 임의로 선택된 단어(negative sampling)와 중심단어의 embedding vector를 내적한 값을 최소로 만든다.
과거 연구에서 SGNS 방법은 내부적으로 중심단어와 문맥단어의 PMI와 관련된 값을 갖는 행렬을 weighted low-rank factorization을 내부적으로 활용한다고 밝혔습니다. PMI(Point-wise mutual information)은 두 사건 사이의 연관성을 측정하는 지표입니다.
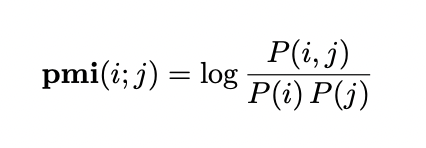
자연어에서는 말뭉치의 co-occurring 빈도 통계량을 활용하여 PMI를 구성하는 확률값을 추정할 수 있습니다.
- x_ij : 중심단어 i와 문맥단어 j가 동시에 등장하는 횟수
- x_i* : summation x_ij with index j = 중심단어 i가 말뭉치에 등장한 횟수
- x_*j : summation x_ij with index i = 문맥단어 j가 말뭉치에 등장한 횟수
- |D| : sumation x_ij with index i and index j = co-occurrence의 총합
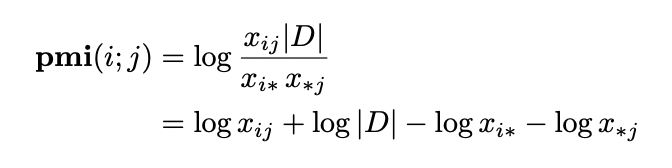
x_ij가 0일 때(i와 j가 같이 등장한 적이 없는 경우)에는 PMI는 음의 무한대로 발산합니다.
SGNS는 W(중심단어 용), W~(문맥단어 용) 2개의 행렬을 만든다고 볼 수 있습니다. W와 W~의 내적은 각 중심단어, 문맥단어 쌍의 PMI 관측값으로 근사할 수 있습니다. SGNS는 (w_i^T)(w~_j) 값과 pmi(i;j) 값의 차이를 하며 관측된 co-occurence 값의 단조증가가중함수인 f(x_ij)를 통해 가중시키며 최소로 만들어야 합니다.
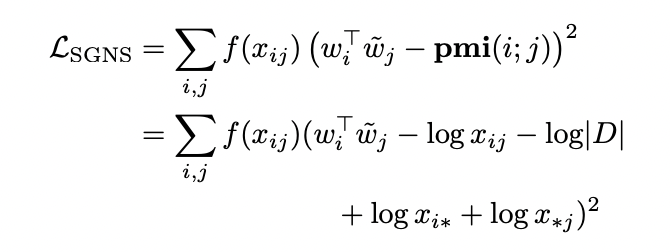
GloVe 는 사전에 계산된 말뭉치의 co-occurence 통계량으로부터 계산을 하는 방법입니다. GloVe는 중심단어 i와 문맥단어 j가 주어졌을 때, 아래의 cost function을 최소화하는 방식으로 학습을 수행합니다. f(x_ij)는 마찬가지로 co-occurence 값인 x_ij의 함수를 통해 cost에 가중치는 부여하는 역할을 합니다.
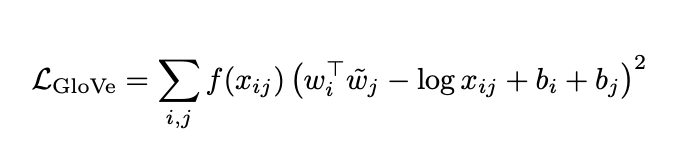
- SGNS와 GloVe 모두 예측값과 co-occurence의 log 값의 차이를 최소화하는 방식을 추구합니다.
- SGNS와 GloVe 모두 co-occurence 값이 클수록 더 큰 penalty를 부여할 수 있도록 f(x_ij)를 cost function에 활용합니다.
3. Swivel
GloVe와 마찬가지로 Swivel은 sampling 대신 co-occurrence 통계량을 사용합니다. SGNS와 마찬가지로 말뭉치에서 대부분의 co-occurrence 값은 관측할 수 없다는 사실을 사용합니다. 두 방법 모두와 마찬가지로 Swivel feature들 간 PMI의 weighted approximate matrix factorization을 활용합니다. 더 나아가 Swivel은 분산처리 환경에서 사용될 수 있습니다.
Swivel은 (m,n) size co-occurrence 행렬에서 출발합니다. 각 row feature(m개)와 column feature(n개)들은 모두 d차원의 embedding vector를 갖습니다. 해당 vector들은 block들로 그룹화되고 그룹화된 vector들은 submatrix shard로 정의됩니다. 학습은 shard를 고르고, 관련된 vector들의 행렬곱을 통해 PMI의 추정값을 얻는 방식으로 수행됩니다. 해당 추정치는 실제 관측된 PMI와 비교되며, co-occurrence값이 존재하지 않을 때는 특별한 방식을 사용합니다. Stochastic gradient descent는 개별 vector들을 update하고 차이를 최소화합니다.
행렬을 여러개의 shard들로 나누는것은 여러개의 worker를 사용할 수 있도록합니다.
3.1 Construction
먼저 각 원소 x_ij가 row feature i와 column feature j 사이의 co-occurence 횟수인 (m,n) size 행렬 X를 만듭니다. row에 사용되는 feature vocabulary는 column에 사용되는 feature vocabulary와 같을 필요는 없습니다.
Row는 feature 빈도를 기준으로 내림차순으로 정렬하고, 계산을 효율적으로 할 수 있는 k 값을 결정하여 k개로 이루어진 row block을 얻습니다. Row는 빈도순으로 정렬이 되어 있기 때문에 동일한 간격으로 sampling된 k개 원소를 갖는 row block는 자주 등장하는 단어와 자주 등장하지 않는 단어가 골고루 포함됩니다.


3.2 Training
학습 이전에, d차원의 feature embedding들은 작은 임의의 값들로 초기화됩니다. (m, d) 크기의 W 행렬은 m개의 row feature(단어)들의 embedding 행렬입니다. (n, d) 크기의 W~ 행렬은 n개의 column feature(단어 문맥)들의 embedding 행렬입니다.


각각의 shard들이 별개로 여겨지더라도 이들은 embedding paramete를 동일한 row block과 column block 내부에서 공유하고 있습니다.
3.3 Training Objective and Cost Function
Swivel은 row feature i와 column feature j의 관측된 PMI 값을 (w_i^T)(w~_j)로 근사합니다. Swivel은 co-occurrence값이 존재하는 것과 존재하지 않는 것을 각각 다루기 위해 piecewise loss function을 사용합니다.

Observed co-occurrences
Co-occurrence값이 0보다 클 때(co-occurence가 있을 때)는 (w_i^T)(w~_j)가 pmi(i;j)를 제대로 근사한다고 여깁니다. 이 때 Swivel은 아래와 같은 loss function을 사용합니다.
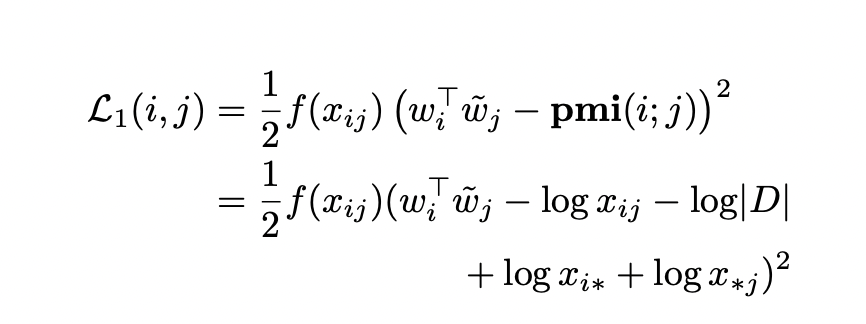
f(x_ij)를 단조증가함수로 사용함으로써 co-occurence값이 클수록 더 높은 penalty를 부여하기 때문에, 추정값(내적값)과 실제값(PMI)의 차이가 더욱 작아져야만 합니다.
Unobserved co-occurrences
만약 feature i와 feature j가 동시에 등장한 적이 없다면, x_ij=0이 되고 pmi(i;j)는 음의 무한대 값을 갖게되어 위에서 정의한 loss function을 계산할 수 없게 됩니다.
이를 해결하기 위해 한 가지 질문을 던질 수 있습니다. Co-occurrence값이 0인것이 얼마나 중요한가? feature i와 feature j 모두 자주 등장하지 않는 단어일때는 co-occurrence가 존재하지 않는 이유는 충분한 양의 data가 존재하지 않기 때문으로 생각할 수 있습니다. 하지만 featrue i와 feature j가 모두 자주 등장하는 단어일 때는 두 feature는 관련이 없다고 생각할 수 있습니다. 두 경우일 때 모두 model이 feature간의 PMI를 과대추정하는 것을 원하지 않기 때문에 PMI 추정치에 upper bound를 사용합니다.
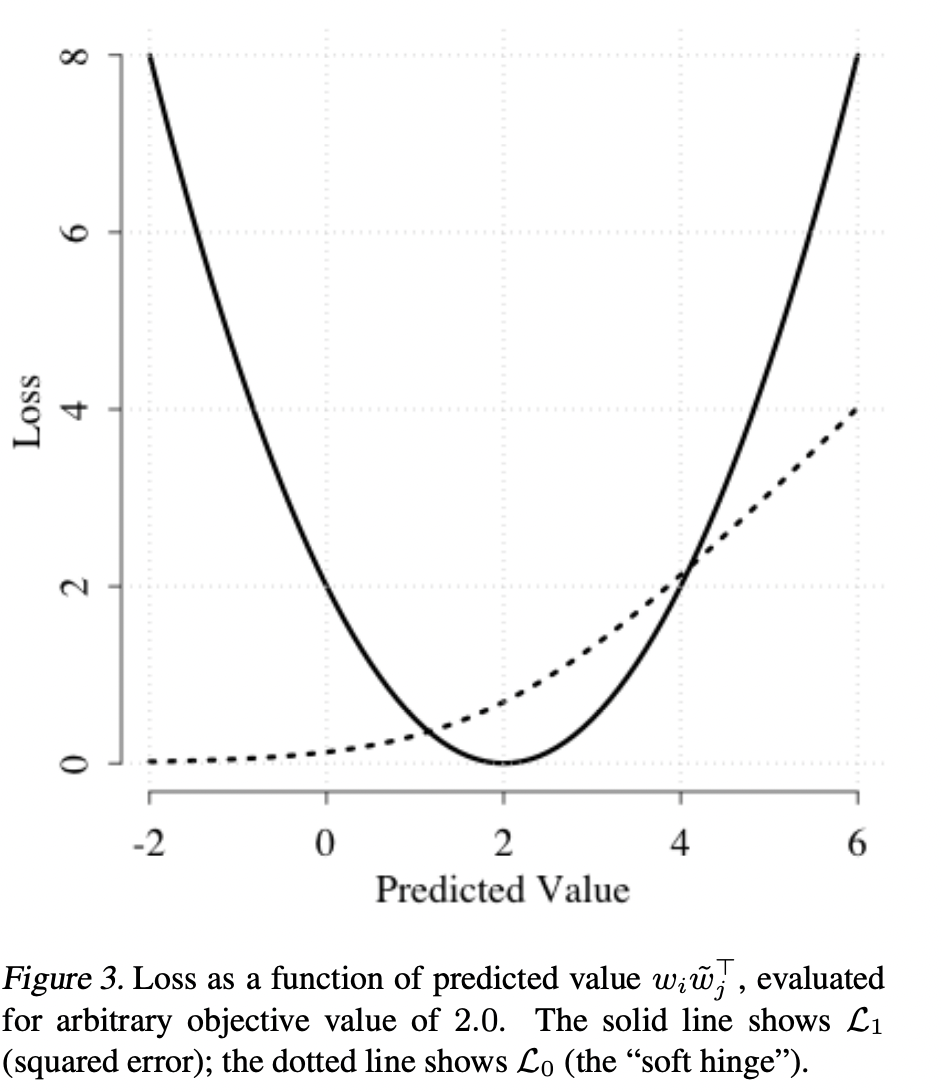
해당 논문에서는 PMI값을 1로 치환하여 smoothing하여 문제를 해결합니다. 그리고 smoothed PMI의 과대추정에 penalty를 주는 asymmetric cost function을 사용합니다. 이를 soft hinge cost function이라 합니다.
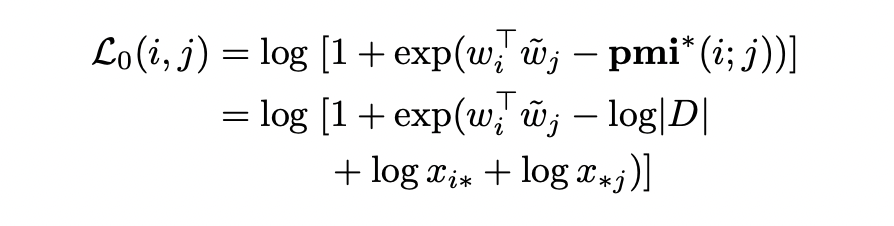
pmi는 smoothed PMI를 의미하며 x_ij가 실제값은 0이지만 1로 치환하여 계산한 결과입니다. 해당 loss는 model이 objective value를 과대추정하지 않도록하는 역할을 합니다.
위의 L_0는 다음과 같이 해석할 수 있습니다. 만약 feature i와 feature j가 자주 등장하는 단어일 때, x_i와 xj 값은 커지게 됩니다. Loss를 줄이기 위해서 model은 작거나 음의 값을 갖는 (w_i^T)(w_j)를 얻어 두 feature 간의 관계가 없음을 나타냅니다. 반면에 만일 feature i와 feature j가 자주 등장하지 않는 단어일 때는, x_i와 x*j 값은 작아지게 됩니다. 따라서 model은 (w_i^T)(w_j) 값이 커지도록 합니다. 이러한 방식을 통해 soft hinge loss는 pmi(i;j)의 추정값이 upper bound를 가질 수 있도록 합니다.
4. Experiments
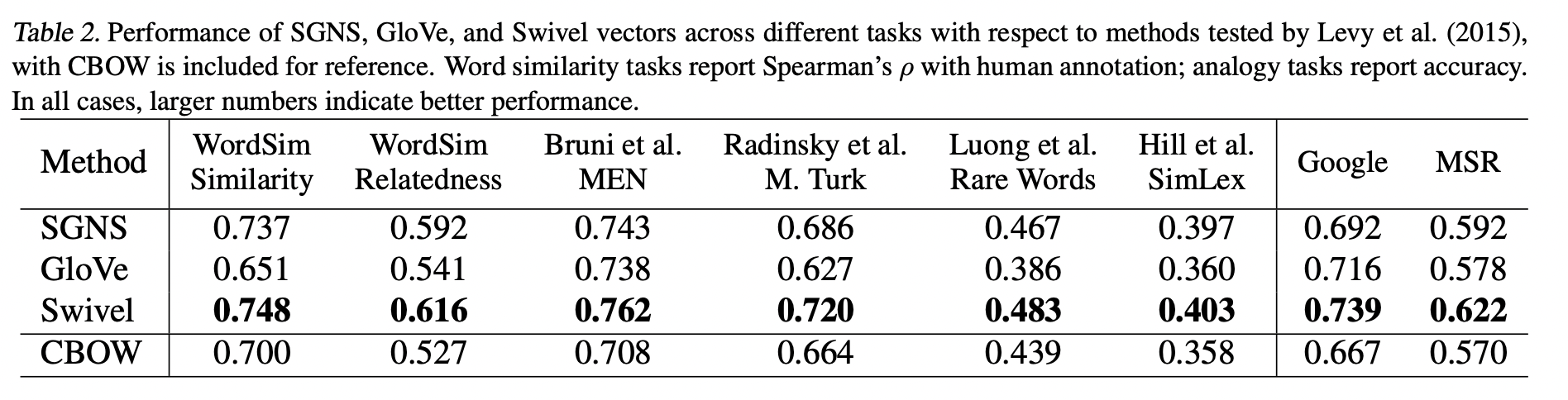
Swivel은 GloVe, SGNS, CBOW 모두보다 좋은 성능을 보였습니다.
해당 논문에서는 이러한 결과가 나온 이유를 SGNS와 Swivel은 unobserved co-occurrence 정보까지 사용했기 때문으로 추정하고 있습니다.


5. Discussion
Swivel은 feature set의 크기가 커지고 training data가 많아짐에 따라 등장하게 되었습니다. 해당 논문에서는 많은 양의 data를 다룰 수 있고, 자주 등장하는 단어와 자주 등장하지 않는 단어 모두에서 좋은 추정ㅇ르 할 수 있기를 원했습니다.
Swivel은 GloVe와 마찬가지로 co-occurrence 통계량으로부터 학습하였습니다.
Swivel은 feature 쌍의 개수가 많아짐에 따라 증가하는 계산량의 증가를 행렬곱을 수행하는 vectorized hardware를 사용하고 matrix를 block 단위로 나눠 여러개의 worker에 분배하여 분산처리를 통해 해결하였습니다.
Swivel은 piecewise loss를 통해 co-occurrence값이 존재할 때와 존재하지 않을 때를 나눠 학습을 수행할 수 있었습니다.
6. Conclusion
Swivel은 co-occurrence 행렬로부터 저차원의 feature embedding을 만들었습니다. Swivel은 중심단어와 문맥단어의 word vector들의 내적값을 두 단어의 PMI 값과 근사시키는 방식으로 최적화되었습니다.
Swivel은 말뭉치의 크기가 아닌 co-occurrence 행렬의 크기에 따라 계산량을 필요로 했기 때문에 더욱 큰 말뭉치를 다룰 수 있었습니다.
Swivel은 모든 co-occurrence 정보(observed co-occurrence + unobserved co-occurrence)를 사용하여 embedding을 만들었습니다. Unobserved co-occrrence일 때는 soft hinge loss를 통해 PMI의 과대추정을 방지하였습니다. 이를 통해 자주 등장하는 단어의 성능을 희생시키지 않으면서도 자주 등장하지 않는 단어의 성능을 높일 수 있었습니다.
Swivel은 block구조를 활용하여 parameter가 늘어남에 따라 증가하는 연산량 tradeoff를 감소시킬 수 있었고, 병렬처리가 가능해져 매우 큰 co-occurrence 행렬을 다룰 수도 있게 되었습니다.