[JS 알고리즘] 빅오 표기법 - 1

빅오 표기법에 대해서..

일단 시작하기전 2개의 함수를 먼저 지정하고 시작하겠습니다.

function addUpTo(n) {
    let total = 0;
    for (let i = 1; i <= n; i++) {
        total += i;
    }
    return total;
}

function addUpTo2(n) {
    return n * (n + 1) / 2;
}

이 두개의 함수는
서로같은 return 값을 가지고 있습니다.
하지만 두개의 코드를 동시에 시작했을때 소요시간은 다릅니다.

function addUpTo(n) {
    let total = 0;
    for (let i = 1; i <= n; i++) {
        total += i;
    }
    return total;
}

function addUpTo2(n) {
    return n * (n + 1) / 2;
}

var t1 = performance.now();
addUpTo(1000000000);
var t2 = performance.now();
console.log(`Time Elapsed: ${(t2-t1) / 1000} seconds `)

performance.now() 함수로 addUpTo()와 addUpTo2()를 비교 했을때
어떤것이 더 나은지 비교했을때 addUpTo2()가 더 빠른 처리시간을 보여줍니다.
하지만 이것은 정확한 비교가 될 수 없습니다.

왜?

함수의 실행속도도 분명히 알고리즘의 성능면에서 비교대상이 될 수 있습니다.
하지만 이것은 상대적입니다.
왜 상대적인가 ?
addUpTo를 실행한 결과를 보겠습니다.

같은 함수를 연속적으로 2회 실행 했는데 값이 다르게 나옵니다.
바로 이것이 상대적인 이유입니다.
모든 알고리즘, 모든 함수가 같은 값을 배출하지만,
모두 다른 시간을 배출합니다. 예를들어 한개의 알고리즘을 실행했을때
어떤컴퓨터는 1초, 어떤 컴퓨터는 3초, 다른컴퓨터는 10초가 걸릴 수 있습니다.
이는 알고리즘의 복잡도와는 달리 컴퓨터의 성능이 값의 배출에 영향을 미칩니다.
이는 매우 상대적인 것으로 알고리즘의 성능 평가에는 적합하지 않습니다.
이 문제점을 해결하기위해 굳이 비교하지 않아도 비교할 수 있는 특정값을 찾기위해 모색된 방법이 바로 빅오 표기법 입니다.

이 빅오표기법은 생각보다 간단합니다.(아직은)
굳이 비교할 필요없이 알고리즘이 몇개의 연산을 처리하는지를 찾으면 알고리즘의 시간복잡도를 계산 할 수 있습니다.

간단하게 얘기해서 서로다른 알고리즘에 값을 넣습니다.
100,1000,10000,100000,1000000 ...
그럼 이렇게 return된 값을 그래프로 그렸을때 빅오표기법에서 표현하는 그래프와 상당히 유사한 모습을 가지고 있습니다.

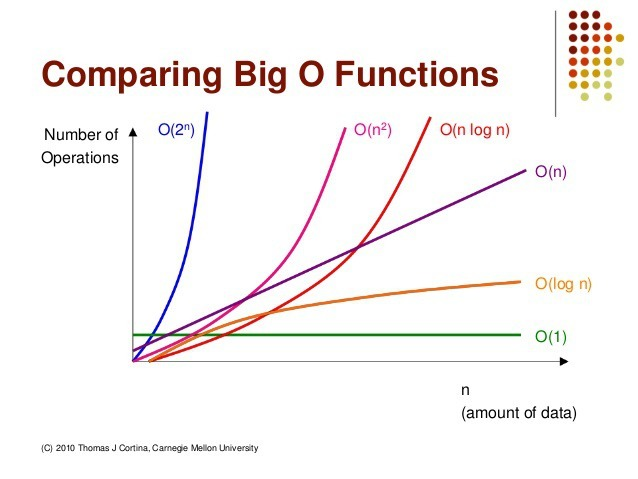
남은 공간복잡도와 나머지 내용은 2편에서 계속 작성 하겠습니다.