미분
import sympy as sym
from sympy.abc import x
func = sym.poly(x**2 + 2*x +3) # 다항식
sym.diff(func, x) # func을 x에 대해 미분* 실행 결과
Poly(2𝑥+2,𝑥,𝑑𝑜𝑚𝑎𝑖𝑛=ℤ)변수의 움직임에 따른 함수값의 변화로 최적화에서 많이 사용된다. 파이썬에서는 sympy 모듈의 diff 함수를 사용해 미분을 할 수 있다.
경사상승법, 경사하강법
함수 의 한 점에서 미분 값을 알면 어느 방향으로 움직여야 함수값이 증가/감소하는지 알 수 있다. 함수값을 증가시키고 싶다면 미분값을 더하고, 감소시키고 싶다면 미분값을 빼면 된다.
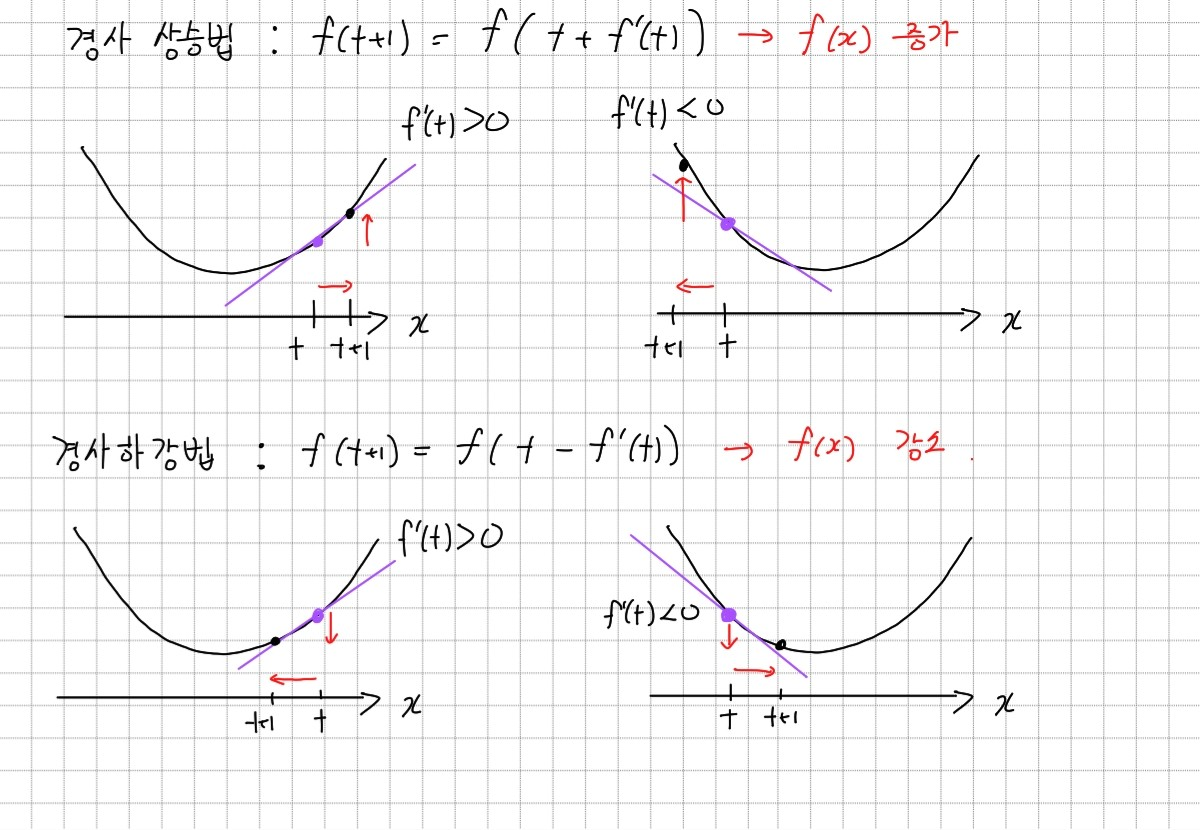
위와 같이 미분값을 더하거나 빼는 것을 반복하면 함수의 극대/극소값에 도달하게 된다. 극값에 도달하면 미분값이 0이 되므로 이동이 멈춘다.
경사 하강법 Pseudo-code
# gradient : 미분값 계산 함수
# init : 시작점, eps : 종료 조건, lr : 학습률
vat = init # 탐색 시작 값
grad = gradient(var) # 미분값 구하기
while(abs(grad) > eps): # 종료 조건까지 이동 반복
var = var - lr * grad # 경사하강법
grad = gradient(var) # 미분값 업데이트컴퓨터로 계산하면 미분이 정확히 0이 되는 것이 불가능하다. 따라서 eps를 종료 조건으로 설정하여 미분값이 eps보다 작아지면 반복을 종료한다. lr은 학습률으로 미분 업데이트 속도를 조절하는데 사용한다.
변수가 여러개인 경우
- 편미분
변수가 벡터인(변수가 여러개인) 다변수 함수의 경우편미분을 사용한다. 편미분은특정 방향 축으로의 이동만 고려하는 것이다. x에 대해 미분한다면 x축 방향으로의 움직임만 고려한다.
import sympy as sym
from sympy.abc import x, y
func = sym.poly(x**2 + 2*x*y +3) # 다항식
print(sym.diff(func, x)) # func을 x에 대해 미분
print(sym.diff(func, y)) # func을 x에 대해 미분실행 결과
Poly(2*x + 2*y, x, y, domain='ZZ')
Poly(2*x, x, y, domain='ZZ')-
gradient vector
각 변수 별로 편미분을 계산하여 벡터로 만든 것을그레디언트 벡터(gradient vector)라고 한다. 그레디언트 벡터를 경사하강법에 사용하면 여러 변수를 동시에 업데이트할 수 있다. -
경사하강법에 적용
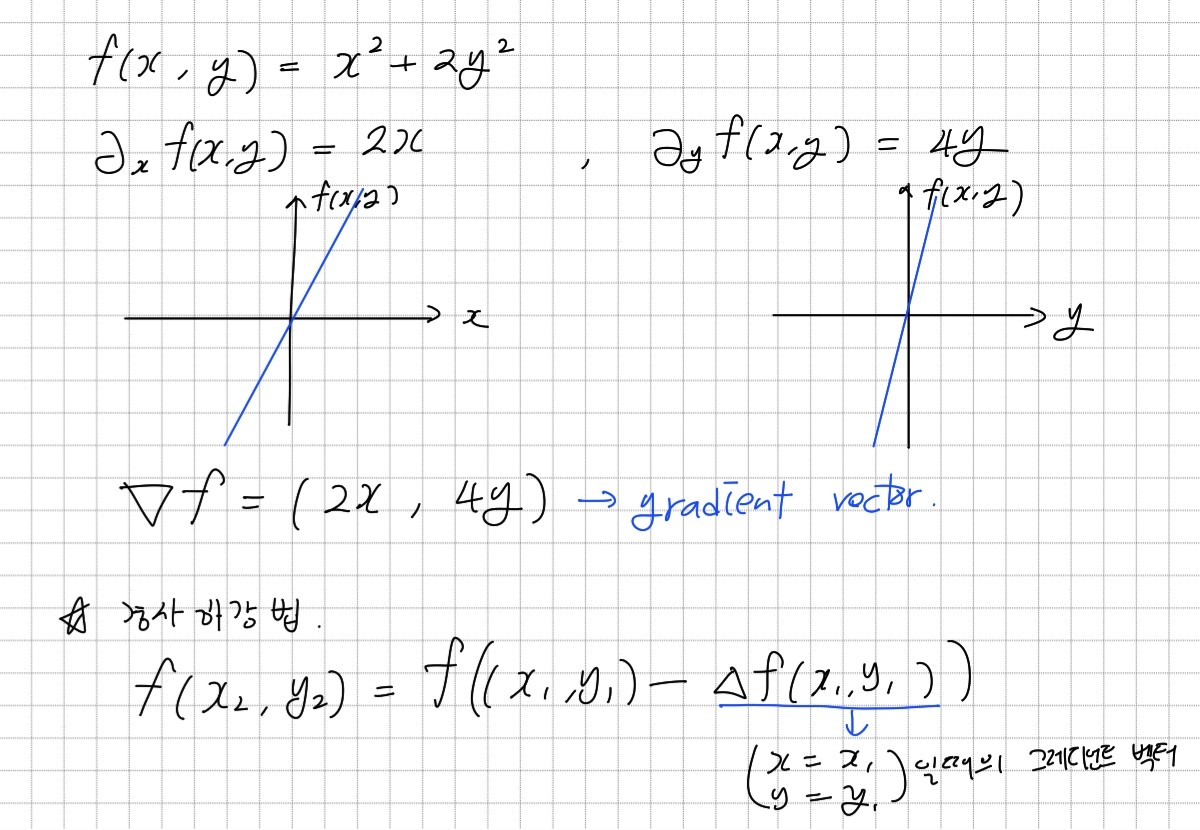
경사 하강법 Pseudo-code
# gradient : 그레디언트 벡터 계산 함수
# init : 시작점, eps : 종료 조건, lr : 학습률
vat = init # 탐색 시작 값
grad = gradient(var) # 미분값 구하기
while(norm(grad) > eps): # 종료 조건까지 이동 반복
var = var - lr * grad # 경사하강법
grad = gradient(var) # 미분값 업데이트경사하강법 기반 선형회귀분석
경사하강법을 사용하면 유사역행렬을 구하지 않고도 선형회귀식을 찾을 수 있다. 경사하강법은 선형 모델 외 다른 모델에도 적용될 수 있는 가장 일반적인 최적화 방법이다.
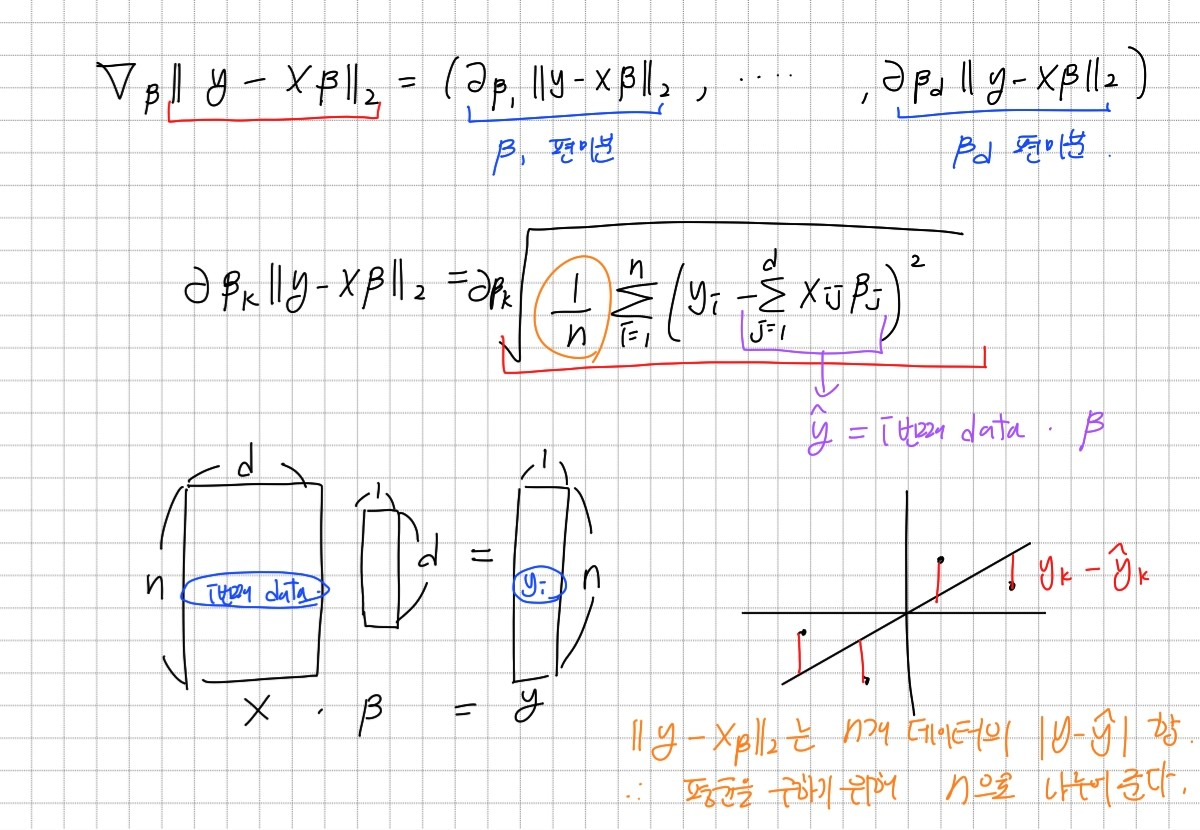
선형회귀식에서 최소화해야 하는 목적식은 2이다. 목적식을 최소화하는 β를 구해야 하므로 위의 그림과 같은 그레디언트 벡터를 사용하여 경사하강법을 적용할 수 있다. 유사역행렬과 달리 그레디언트 벡터를 사용하여 정답으로 점차 다가가는 방식이기 때문에 학습률과 학습횟수가 중요하다.
확률적 경사하강법
경사하강법은 미분가능하고 볼록 함수에 대해서는 학습률과 학습횟수를 적당히 조절하여 최소값으로 항상 수렴할 수 있다. 하지만 볼록함수가 아닌 경우 극소값에 도달할 수는 있지만, 최소값은 아닐 수도 있다.확률적 경사하강법은 이러한 문제를 해결하기 위해 모든 데이터를 사용하는 것이 아니라 일부 데이터만 사용해 그레디언트 벡터를 생성하고 값을 업데이트한다.
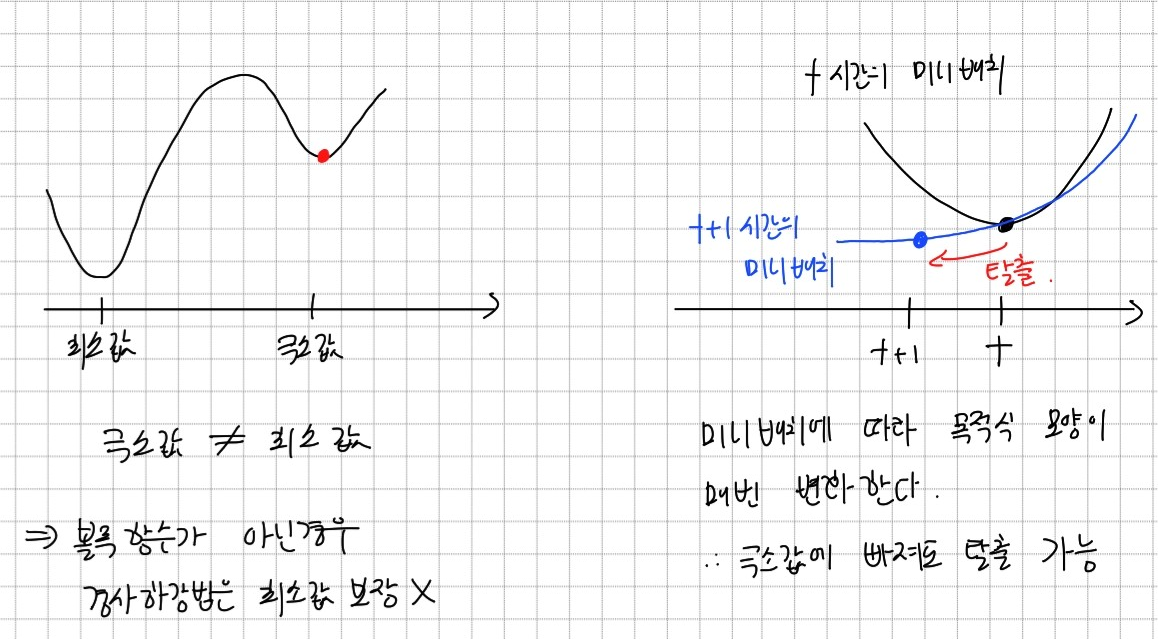
일부 데이터를 미니 배치라고 하며, 미니 배치를 사용하면 연산량이 감소하고 볼록 함수가 아닌 함수에서도 최소값으로 수렴할 수 있다. 미니 배치는 확률적으로 선택하므로 목적식 모양이 매번 변경된다. 따라서 이전 미니 배치에서 최소값이 아닌 극소값에 빠져도 목적식 모양이 변경되어 빠져 나올 수 있게 된다. 다만 미니 배치 사이즈가 너무 작으면 경사하강법보다 더 늦게 최소값에 수렴할 수 있으니 주의해야 한다.
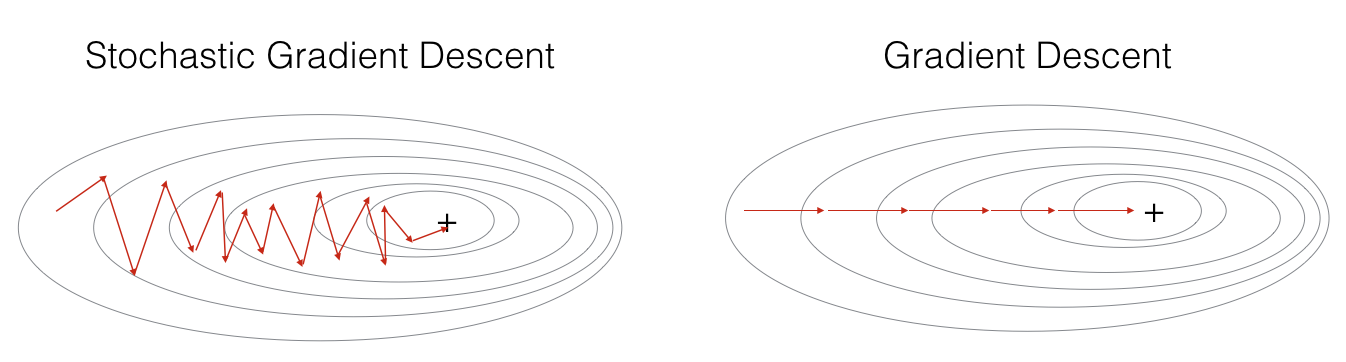
확률적 경사하강법은 경사하강법처럼 항상 최소값 방향으로 이동하지는 않는다. 하지만 이동 경향이 최소값으로 향하는 경향을 띄며 이동 방향 계산이 경사하강법보다 훨씬 빠르다.
경사하강법의 입력 데이터가 매우 큰 경우 하드웨어의 한계로 인해 메모리 부족이 발생할 수 있다. 알고리즘 효율성 또한 더 적은 데이터를 사용하여 계산하는 확률적 경사하강법이 더 좋다. 이러한 이유로 경사하강법은 딥러닝에서 사용하기에는 어려움이 있다.
참고
경사하강법 : https://datascience-enthusiast.com/DL/Optimization_methods.html