[AI Math] 행렬

행렬

x = np.array([[1,2,3],[4,5,6],[7,8,9]])

행렬은 벡터를 원소로 가지는 배열이다. 벡터를 행벡터로 표현하기 때문에numpy에서는 행(row)이 기본 단위가 된다. 행(row)과 열(col) 인덱스를 가진다.

행렬 연산

x = np.array([[1,2,3],[4,5,6],[7,8,9]])
y = np.array([[10,11,12],[13,14,15],[16,17,18]])

print(x * 3)  # 스칼라 곱
print(x + y)  # 덧셈
print(x - y)  # 뺄셈
print(x * y)  # 성분 곱

행렬이 같은 모양이면 덧셈, 뺄셈, 성분 곱 연산이 가능하다. 벡터와 같이 같은 위치의 성분끼리 연산이 이루어진다.

x = np.array([[1,2,3],[4,5,6],[7,8,9]])
y = np.array([[10,11,12],[13,14,15],[16,17,18]])

print(x@y)  # 행렬 곱
print(np.inner(x, y))  # i번째 행벡터 * j번째 행벡터

행렬 곱셈은 첫번째 행렬의 i번째 행벡터와 두번째 행렬의 j번째 열벡터의 내적을 (i, j)번째 성분으로 가지는 행렬을 계산한다. 따라서 다른 곱셈 연산과 달리 곱셈의 순서가 바뀌면 결과가 달라진다. @ 연산자를 사용하여 행렬 곱셈을 할 수 있다.
numpy의 inner 함수는 첫번째 행렬의 i번째 행벡터와 두번째 행렬의 j번째 행벡터의 내적을 (i, j)번째 성분으로 가지는 행렬을 계산한다.

행렬 이해 1 - 데이터 모음

벡터는 공간 상의 한 점을 의미한다. 따라서 벡터가 여러개 모여 있는 형태인 행렬은 공간 상 여러점이 모여있는 형태가 된다. 이때 공간 상 점을 데이터라고 해석하면, 행렬은 여러 데이터의 모임이 된다. 행렬의 i 번째 행벡터는 i 번째 데이터를 의미한다.

행렬 이해 2 - 벡터 공간 연산자

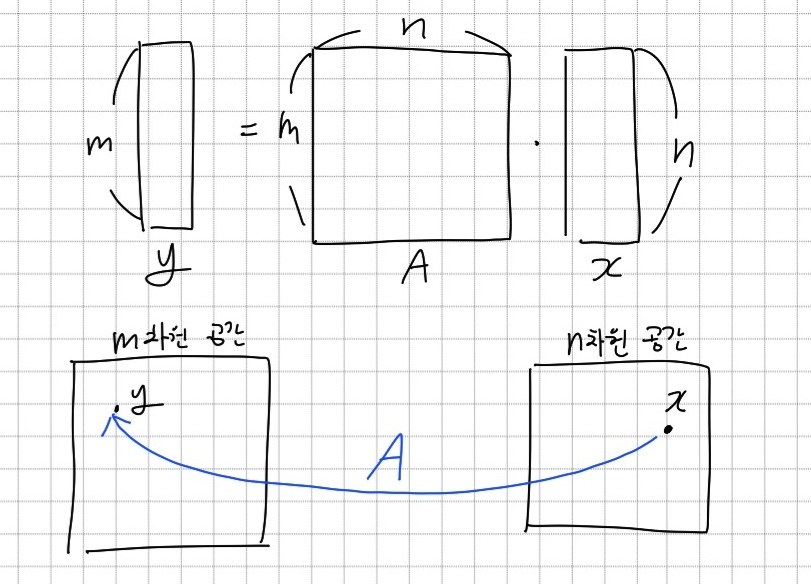
행렬을 벡터공간의 연산자로 생각할 수 있다. 위의 그림에서 같이 n차원 공간의 벡터 x를 m차원 공간의 벡터 y로 변형시키는 역할을 행렬 A가 하고 있다. 이처럼 행렬을 벡터와 곱해져 벡터를 다른 차원의 공간으로 보내는 연산자로 이해할 수 있다.

역행렬

AA-1 = A-1A = I

위의 수식을 만족하는 A-1를 A의 역행렬이라고 한다. 행렬을 벡터 공간 연산자라고 생각했을 때 A-1는 행렬 A의 연산을 거꾸로 되돌리는 연산을 한다.

역행렬이 존재할 수 있는 조건은 다음과 같다.

	1. 행과 열의 숫자가 같은 정방행렬
	2. 행렬식(determinant) != 0

파이썬 코드에서 역행렬은 linalg 모듈의 inv 함수를 사용하여 구할 수 있다.

x = np.array([[1,2,3],[4,5,6],[7,8,9]])

np.linalg.inv(x)	# 역행렬 

유사역행렬 (presudo-inverse)

역행렬을 계산할 수 없는 경우 유사역행렬(presudo-inverse) $A^+$을 사용한다.

• 행 > 열
  $A^+$ = $(A^TA)$-1$A^T$
  $A^+$A = I
• 행 < 열
  $A^+$ = $A^T$(A$A^T$)-1
  A$A^+$ = I

유사역행렬은 행과 열 중 더 큰 값이 무엇인지에 따라 성립하는 식이 달라지므로 주의해야 한다. 유사역행렬을 사용하면 연립 방정식, 선형회귀분석 문제를 풀 수 있다.

• 연립 방정식
  
  주어진 식보다 변수가 더 많은 경우 일반적으로는 해를 구할 수 없다. 무수히 많은 해가 존재하기 때문이다. 이런 경우 유사역행렬을 사용하여 무수히 많은 해 중 하나를 구할 수 있다.

• 선형회귀분석
  선형회귀분석은 데이터 X와 결과값 y가 주어졌을 때 계수 b를 잘 조정하여 선형회귀식을 찾아야한다. 선형회귀분석은 계수의 개수보다 데이터의 개수가 더 많다. 즉 변수 개수보다 식의 개수가 더 많은 것이다. 따라서 모든 식을 만족시키는 계수 b의 값을 찾을 수 없다.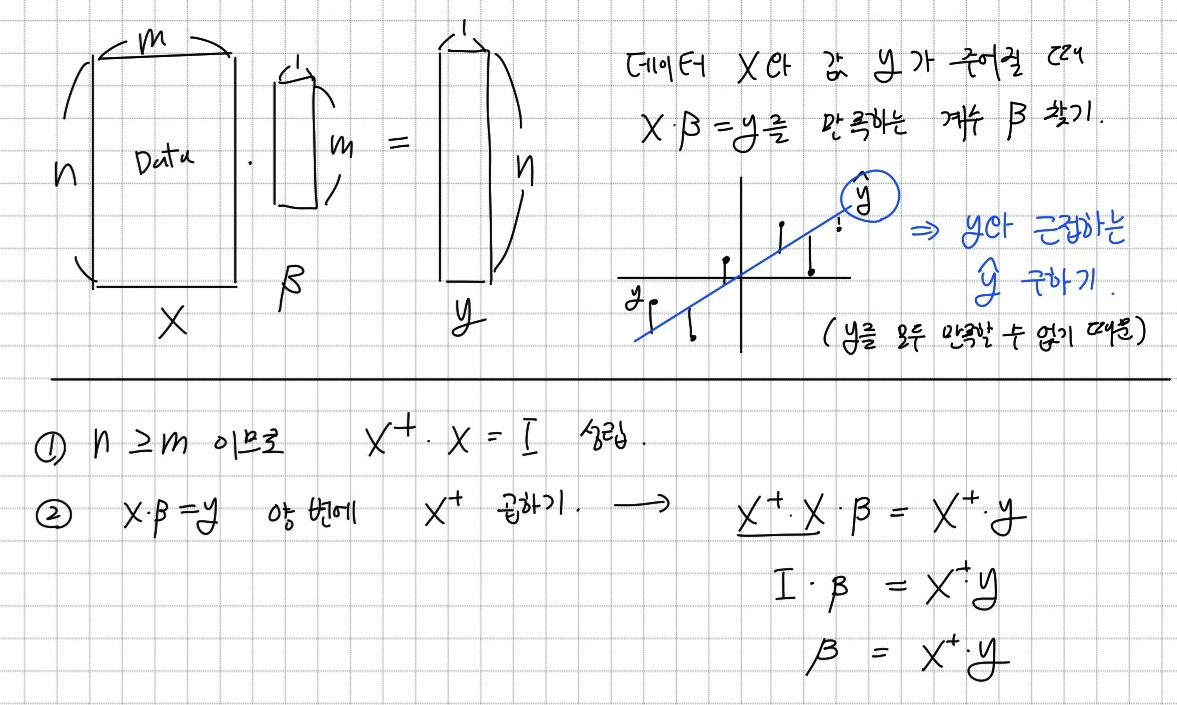
  유사역행렬을 사용하면 모든 y를 만족하지는 않지만 y와 근접한 y^을 만족하는 계수 β를 구할 수 있다.