03. Optimization (부제: 딥러닝 용어 정리)
AI TechBaggingBoostingDeep LearningGradient DescentOptimizercross validationgeneralizationoverfitting딥러닝 용어 정리부스트캠프
Deep Learning Basic
목록 보기
4/4

최적화 용어에 대하여 명확한 이해가 필요하다!
면접때 이 부분을 묻는 질문이 많이 나올 것이라고 예상된다.
Introduction
Gradient Descent

- First-order iterative optimization algorithm for finding a local minimum of a differentiable function.
- 미분 가능한 함수의 local minimum(극소)을 찾기 위해 1차 편미분을 반복적으로 하며 update하는 방법
Important Concepts in Optimization
Generalization
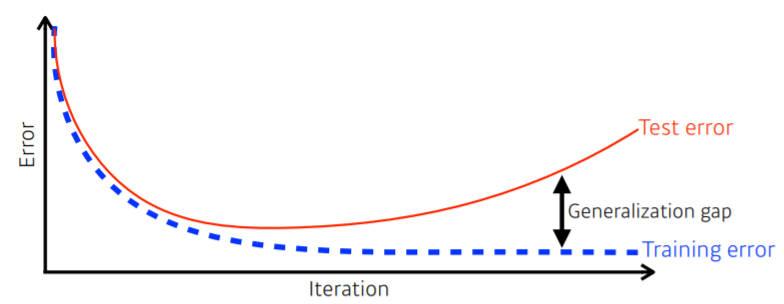
- 목적: 일반화 성능을 높여보자!
- Generalization performance: Train/Test error간의 차
Generalization performance가 좋다?
- 성능이 Train data와 비슷함을 보장한다!
- 하지만 training error가 높지만 Generalization performance가 좋다면 성능을 보장할 수 없다.
따라서 Generalization performance가 좋다고 해서 모델의 성능이 좋다는 것을 의미하는 것은 아니다!
Under-fitting vs. over-fitting
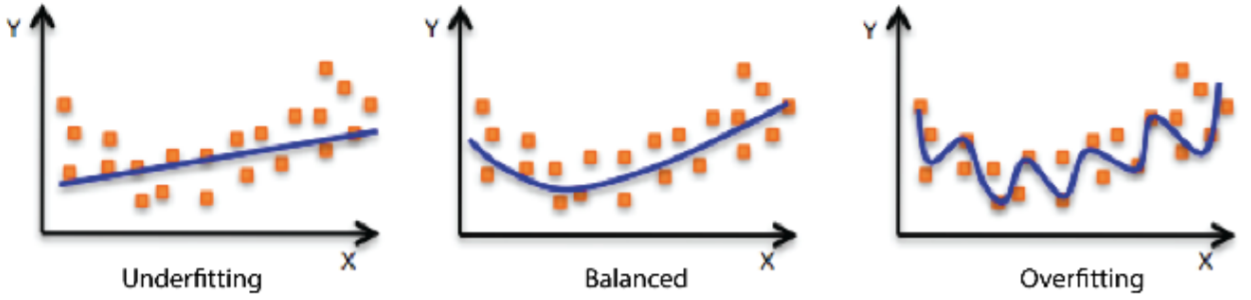
- 개념적인 이야기이기 때문에 판단 기준은 절대적이지 않음에 유의!
Overfitting: 과적합
- train data에서는 성능이 잘 나오지만, test data에는 잘 동작하지 않 는경우.
Underfitting: 과소적합
- 적게 학습되어서 train data도 잘 맞추지 못하는 경우.
Cross validation (k-fold)
validation set
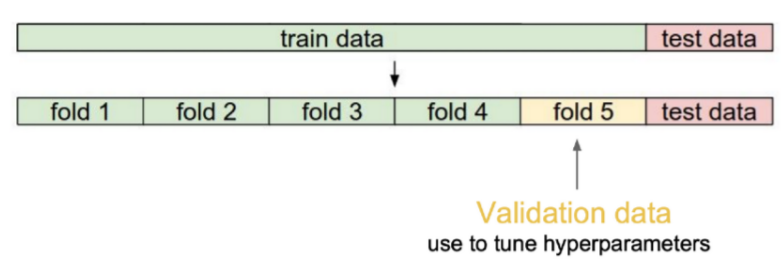
- 보통 train data와 test data를 나눈 후 train data의 일부를 validation data로 둔다.
- 이 때 validation data를 hyperparameter tuning하기 위해 사용한다.
k-fold
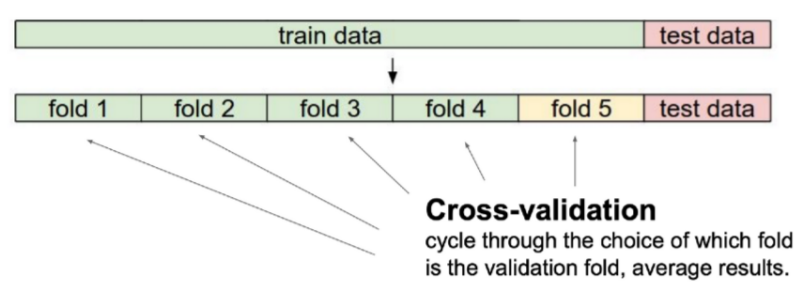
- test data를 제외한 data를 k개로 나누어서 k-1개를 train에, 1개를 validation 용도로 사용한다.
- 성능을 제대로 검증하기 위하여 validation set을 바꿔가면서 test하는 방법이다.
- 당연히 test는 사용하지 않는다.
Bias and Variance
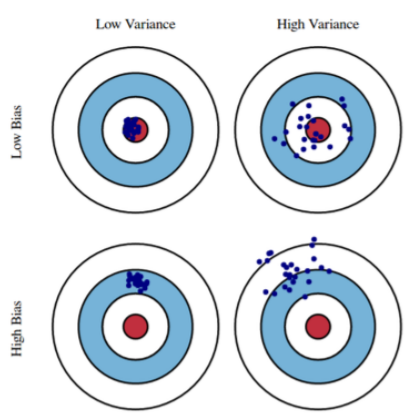
Bias
- 평균적으로 봤을 때 True Target(정답, 그림에서 빨간 부분)에 얼마나 접근했는지?를 나타낸다.
- 분산과 관계 없이, 점들의 평균치가 과녁 중앙에 가까이 갔으면 bias가 낮은 것이다.
- Low Bias: 평균적으로 봤을 때 True Target에 접근
- High Bias: True Target에서 많이 벗어남
Variance
- input을 넣었을 때 output이 얼마나 일관되게 나오는가?
- Low variance: 같은 곳에 찍힘, 일관적
- High variance: input에 비해 output이 비교적 크게 바뀜, overfitting 될 가능성 존재
Bias and Variance Tradeoff
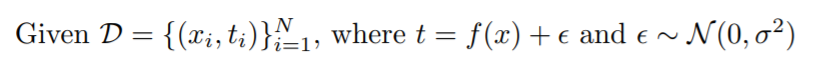
내 학습 data에 noise가 있을 경우...
- : True Target(정답)

- cost를 식을 bias, variance, noise로 풀어 쓸 수 있다.
- 하지만 bias와 variance는 trade-off 관계이다.
- 따라서 이 모두를 줄이기는 힘들다...!!
