
Coordinate Systems
World Coordinate
- 수직벡터로 동차좌표계로 표현
- 우주의 중심축
View Coordimate
- 월드 좌표에 View Transform Matrix 'M'을 곱하면
카메라 위치의 상대적 좌표인 View Coordinate 로 변함
Normalized Coordinate
- 뷰 좌표계에서 Projection Matrix 'P'를 곱하면 우리가 보는 화면 영역의 -1 ~ 1 사이로 바뀌게 됨
World Coordinate에서 오브젝트가 이동한다면?
- 이동할 때마다 모든 점의 좌표를 바꾸어주는 것은 비효율적
- 원래 위치에다가 Mw라는 변환행렬을 곱해주면 이동한 위치로 바뀜
버텍스 버퍼에서 모든 저에 일일히 좌표를 더하면 CPU에서 하는데, 변환행렬을 곱하는 방식은 GPU에서
수천개의 코어가 동시에 병렬적으로 돌아가면서 계산하므로 훨씬 더 빠름 - 그리고 M을 곱해주기 전에 먼저 곱해주어야 함 (행렬계산은 왼쪽에서 오른쪽으로 수행)
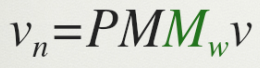
- 여러 개의 물체가 있으면 물체마다 Mw가 다르게 존재
- 이후 View Coordinate로 변환하기 위한 행렬 M은 카메라의 위치에 의해서 결정되므로 물체마다 다르진 않음
- 이후 Normalized Coordinate으로 변환하기 위한 행렬 P도 카메라 렌즈가 perspective/orthogonal 방식인지에 대한 차이이기 때문에 물체마다 다르진 않음
Local -> World Coordinate
이동행렬 Mw가 R x T이면 T만큼 먼저 이동한 다음 R만큼 회전하는 것 (이동은 로컬축, 회전은 월드축)
이동행렬 Mw가 T x R이면 R만큼 먼저 회전한 다음 T만큼 이동하는 것 (회전은 로컬축, 이동은 월드축)
즉, R을 기점으로 회전축이 바뀌어서 R 전에 이동할 경우 로컬축 이동이고, R 후에 이동할 경우 월드축 이동
General Transform
- 카메라의 위치가 Mv^-1만큼 움직였을 때, 카메라가 고정되어 있으면 월드가 Mv만큼 이동한 것
Transformation Order
- Mw를 곱하기 전에는 모든 게 로컬좌표, Mw를 곱하고 나면 월드좌표로 바꿈.
ex. Mw를 곱하기 전에 이동행렬을 곱하면 로컬축 이동이고, Mw를 곱한 후에 이동행렬을 곱하면 월드축 이동임
Q. 만약 물체를 회전한다고 할 때 다음 상황에서 수식이 어떻게 되어야할지?
Mw는 world transform matrix, Mv는 view transform matrix, P는 projection matrix
- World coordinate 의 축으로 회전: P Mv R * Mw
- Local coordinate 의 축으로 회전: P Mv Mw * R
- View coordinate 의 축으로 회전: P R Mv * Mw
Relative Coordinate?
각 물체를 붙어있는 다른 물체의 상대적인 위치로 표현
- Multiple Coordinate Transformation
- Hierarchical Transformation
- 대표적인 예시는 로봇인데, Base 만 바뀌어도 팔의 위치가 변하게 됨
- 또 다른 예시로는 책상위의 물체. 책상이 움직이면 그 위의 물체도 같이 움직여야 함
각 물체를 붙어있는 상대적 위치로 만들기 위해 계층 구조를 만들 수 있음
각 물체의 위치를 저장하는 자료구조?
Matrices
- Mw, Mv, Mp는 각각 가지고 있는 것이 좋고, 특히 Mw는 물체마다 따로 가지고 있어야 한다.
- Mw는 물체가 이동하면 달라지고, Mv는 카메라의 위치가 변할 때 달라지고, Mp는 스크린의 투영 방식이 바뀔 때 달라진다.
Matrix는 OpenGL에서 쓰기에 좋은데, 행렬만 보고 현재 위치나 방향을 알기는 어려움
대안
- 이동은 Vector3로, 회전은 Quaternion으로 표현!
- 이동은 월드좌표계 중심으로, 회전은 로컬좌표계 중심으로
월드좌표계에서의 움직임을 표현하기 위해서는 행렬 표현이 더 좋기는 함
정리
Coordinate Transformation
- Matrix 또는 Rotation + Translation 으로 표현 가능
- 물체의 이동은 Rotation/Translation을 현재의 정보에 추가로 곱해주거나 더해주는 것
- 이동은 쉽고 회전은 이해하기 어려워서, 회전행렬을 다른 방식 (Quaternion)으로 바꾸는 게 필요
Local Coordinate System
- 여러 오브젝트들을 쉽게 조정하기 위해 존재
- 마찬가지로 Matrix 또는 Rotation + Translation 으로 표현 가능
- Rotation과 Quaternion 관계 중요
