평가지표

분류(Classification) 평가 지표

1. 정확도 (Accuracy)
2. 정밀도 (Precision)
3. 재현률 (Recall)
4. F1점수 (F1 Score)
5. PR Curve, AP score
6. ROC Curve, AUC score

• 다중 분류(Multi class classification)
• 이진 분류(Binary classification)
  • 양성(Positive): 찾으려는 대상. 보통 1로 표현
  • 음성(Negative): 찾으려는 대상이 아닌 것. 보통 0로 표현
• 정확도 : accuracy_score(정답, 모델예측값)
  • 양성(Positive)에 대한 지표만 확인할 수 있음 (클래스별 성능X)

---

MNIST Data set : 손글씨 숫자 데이터 셋

from sklearn.datasets import load_digits

import numpy as np
import matplotlib.pyplot as plt

mnist = load_digits()
mnist.keys()

X, y = mnist['data'], mnist['target']
X.shape, y.shape, type(X), type(y)
# X의 shape : (1797, 64) -> 이미지 :1797개, 구성 : 64개값의 1차원 배열

# X: image -> 8 X 8 2차원배열의 이미지를 flatten(1차원으로 reshape) 한 형태로 제공된다.

---

Dummy Model

• 모델을 흉내낸 모델

• 내가 예측한 그대로 출력

• Target Label중 무조건 최빈값으로 예측

  → 불균형 레이블 데이터세트의 평가지표로 정확도만 보면 안됨, 특히 Positive에 대한 예측이 중요한 경우에는 accuracy는 알맞은 평가 지표가 아님

---

혼동 행렬(Confusion Marix)

• 분류 문제에서 모델이 예측한 결과와 실제 레이블을 비교하여 각각의 예측 결과에 대한 정보를 시각화하는 표 형태의 행렬
  
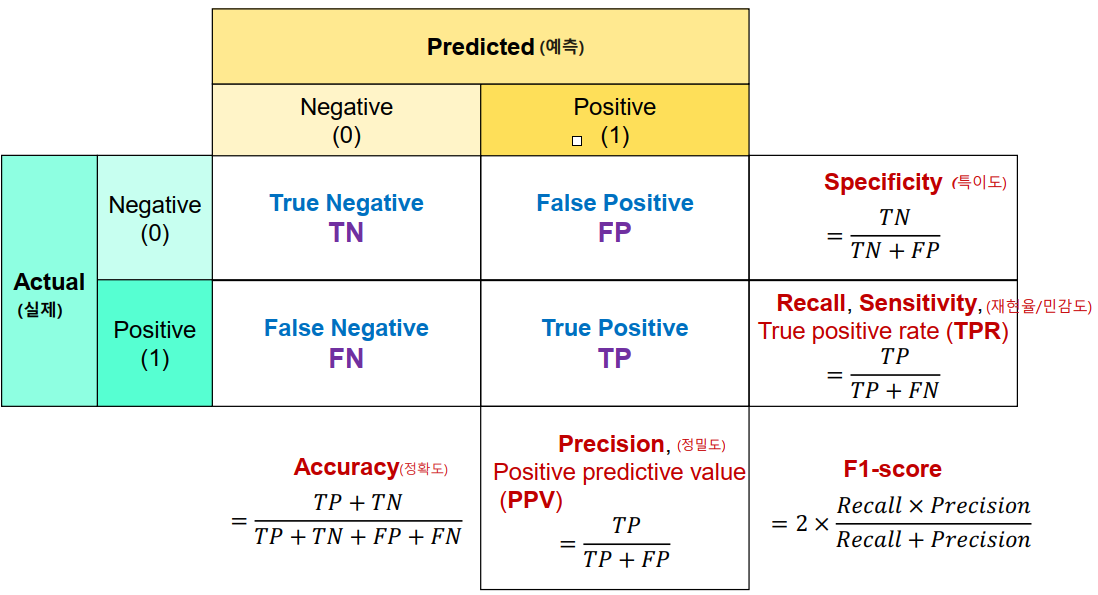
• confusion_matrix(정답, 모델예측값)
• 이진 분류 평가지표 (이진분류 뿐아니라 모두 가능하지만 대표적으로)
  • 양성(Positive) 예측력 측정 평가지표

    • Recall/Sensitivity(재현율/민감도) = TPR

      recall_score(y 실제값, y 예측값)

      → 정답이 양성인 것 중에서 양성으로 예측한 것- 

    • Precision(정밀도) = PPV

      **`precision_score(y 실제값, y 예측값)`**
      
      
        → 양성으로 예측 한 것 중에서 실제 양성인 것

      → 1이라고 하는 것은 다 맞는 것

    • F1 점수

      f1_score(y 실제값, y 예측값)

      → 정밀도와 재현율의 조화평균 점수

      → recall과 precision이 비슷할 수록 높은 값 ⇒ 둘 다 좋아야 함
      

    • classification_report(y 실제값, y 예측값)

      → 클래스 별로 recall, precision, f1 점수와 accuracy
      

  • 음성(Negative) 예측력 측정 평가지표
    • Specificity(특이도) = TNR → 실제 음성인 것 중에서 음성으로 예측한 것(재현율의 음성 버전)
      
    • Fall out(위양성률) = FPR → 실제 음성인 것 중에서 양성으로 잘못 예측한 것의 비율 → 1 - 특이도
      
  • 재현율과 정밀도의 관계
    • 재현율이 중요한 이유
      • 실제 양성 데이터를 음성으로 잘못 판단하면 큰 영향이 있는 경우
      • 양성을 놓치지 않는 것에 중점, FN에 초점
      • ex) 질병 유무 판단
    • 정밀도가 중요한 이유
      • 실제 음성 데이터를 양성으로 잘못 판단하면 큰 영향이 있는 경우
      • 양성 예측의 정확성에 중점, FP에 초점

---

임계값(Threshold)

• 이진 분류 모델에서 양성(Positive) 또는 음성(Negative)으로 예측할 때 사용되는 기준값

• 임계값을 변경하면 양성으로 분류되는 샘플의 비율이 변하므로, 이는 정밀도와 재현율에 영향을 미침
  

  임계값▼ → 재현율▲ 정밀도▼
  임계값▲ → 재현율▼ 정밀도▲

• 임계값의 변경은 업무 환경에 따라 두 수치를 상호보완할 수 있는 수준에서 적용되어야함

---

PR Curve & AP Score

• PR Curve(정밀도-재현율 곡선)
  1. 모델의 예측 결과를 기반으로 예측 확률이 높은 순서대로 샘플을 정렬
  2. 임계값을 변경하면서 각 임계값에서의 정밀도와 재현율을 계산
  3. 계산된 정밀도와 재현율 값을 기반 그래프 - 곡선이 좌측 상단에 가까울수록 모델의 성능이 우수, 늦게 꺾어질 수록 좋은 모델
• AP Score(Average Precision Score)
  • PR Curve 아래 영역의 면적을 계산한 값
  • 모델의 정밀도-재현율 곡선에 대한 평균적인 성능
  • 모든 재현율 값에서의 정밀도를 고려하여 계산, 높은 재현율에서의 정밀도가 중요
  • Average Precision은 0과 1 사이의 값을 가지며, 1에 가까울수록 모델의 성능이 우수

from sklearn.metrics import (precision_recall_curve, # threshold 변화에 따른 recall/precision 값들을 계산하는 함수
                             PrecisionRecallDisplay,  # PR Curve를 그리는 클래스
                             average_precision_score) # AP Score 계산 함수

---

ROC curve & AUC score

• ROC Curve(수신자 조작 특성 곡선)
  • 위양성율(False Positive Rate, FPR)에 대한 재현율/민감도(True Positive Rate, TPR )의 곡선
  • 위양성율 : 낮을수록 좋음
  • 재현율 : 높을수록 좋음
  1. 모델의 예측 결과를 기반으로 양성 예측 확률이 높은 순서대로 샘플 정렬
  2. 임계값을 변경하면서 각 임계값에서의 TPR과 FPR 계산
  3. 계산된 TPR과 FPR 값을 기반 그래프
  • 임계값이 변경되면서 TPR과 FPR이 비례해서 변화
• AUC(Area Under the Curve)
  • ROC Curve의 면적, 0과 1 사이의 값
  • 1에 가까울수록 모델의 성능이 우수
  • 모델의 정렬 능력을 나타내며, 무작위로 선택한 양성 샘플과 음성 샘플 간의 순서를 올바르게 예측할 확률로 해석
    • 0.5에 가까울 경우, 모델의 성능은 무작위 예측과 비슷
    • 1에 가까울수록 모델은 거의 모든 경우에 대해 올바른 순서로 예측하는 능력
  • AUC 점수기준
    • 1.0 ~ 0.9 : 아주 좋음
    • 0.9 ~ 0.8 : 좋음
    • 0.8 ~ 0.7 : 괜찮은 모델
    • 0.7 ~ 0.6 : 의미는 있으나 좋은 모델은 아님
    • 0.6 ~ 0.5 : 좋지 않은 모델

회귀(Regression) 평가지표

1. MSE (Mean Squared Error)
2. RMSE (Root Mean Squared Error)
3. 𝑅2 (결정계수)

• MSE (Mean Squared Error)
  • 예측 값과 실제 값 간의 차이를 잘 보여주며, 값이 작을수록 모델의 예측이 정확
  • scikit-learn 평가함수: mean_squared_error()
  • 교차검증시 지정할 문자열: neg_mean_squared_error
• RMSE (Root Mean Squared Error)
  • MSE의 제곱근이 RMSE
  • MAE(Mean Absolute Error) - 오차 절대값의 평균
    • 예측 값과 실제 값 간의 절대적인 차이
    • 값이 작을수록 모델의 예측이 정확함
    • mean_absolute_error()
    • neg_mean_absolute_error
• 𝑅2 (R square, 결정계수)
  • 평균으로 예측했을 때에 비해 모델이 예측했을 때 얼마나 개선됐는지 보는 것
  • 모델이 종속 변수의 변동 중 얼마나 설명할 수 있는지를 나타내는 지표
  • 1에 가까울 수록 좋은 모델
  • scikit-learn 평가함수: r2_score()