[데브코스] Bias-Variance Trade-off

<데브코스 9주차 day1 선형회귀3 - 강창성 강사님>
현실의 모든 데이터는 완벽할 수 없으므로 노이즈(시그마)가 껴있다.

• 아래와 같은 손실함수 MSE를 Bias-Variance Decomposition하면 Bias^2 + Variance + noise로 나눌 수 있다.
• 따라서 Loss를 최소화하는 방법에는 Bias or Variance를 최소화하는 방법이 있따.

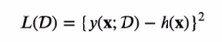
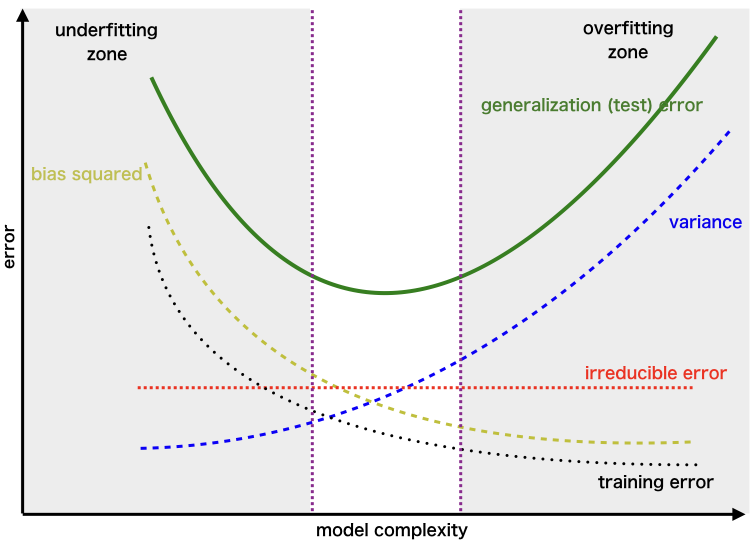
하지만 Bias와 Variance는 Trade-off의 관계로 모델이 복잡해질 수록(학습이 진행 될 수록)Bias는 낮이지게 되지만 Variance는 높아지게 된다.
따라서 Bias_error와 Variance_error의 합이 낮아지는 점을 적절히 찾는 것이 General한 모델을 찾는거라 할 수 있따.

• 아래의 그래프는 sin(2πx) 함수
  • 람다는 규제함수 상수 (람다가 높을수록 높은 규제)
  • 왼쪽 표는 Variance 오른쪽 표는 Bias
    
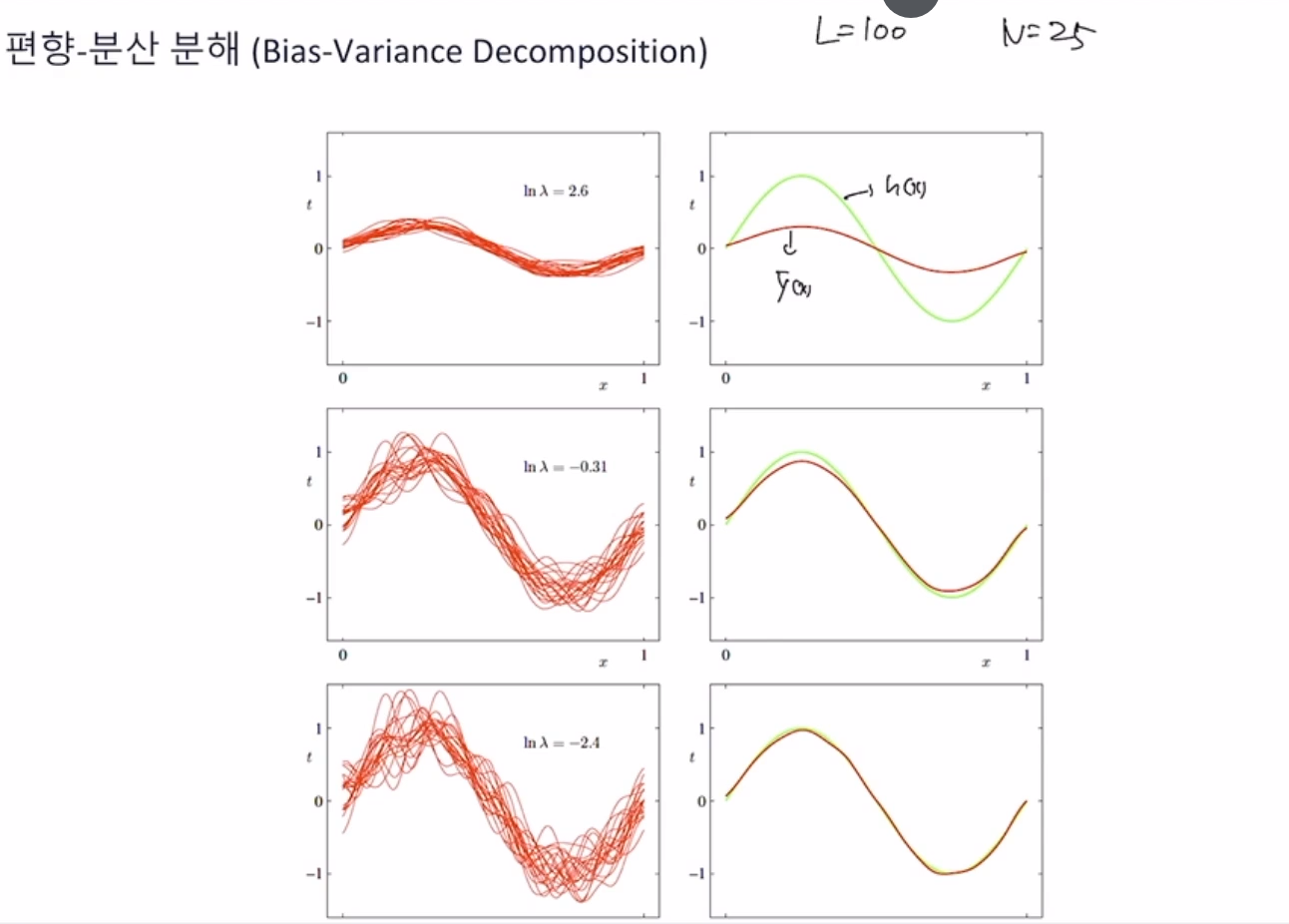
• 1행의 그래프는 낮은 variance_error 높은 bias_error를 보인다.
• 2행의 그래프는 둘다 적절해 보인다.
• 3행은 높은 variance_error 낮은 bias_error를 보인다.
  • 3번째 모델이 sin(2πx)에 근접하게 근사했으니 가장 좋은 모델이 아닐까?
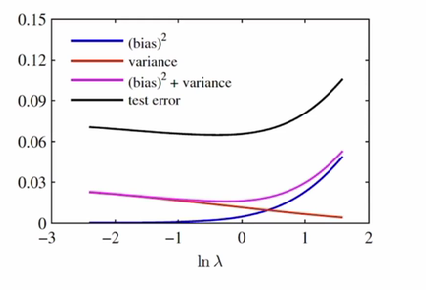
    결과 : 3번째 행의 모델은 위의 그래프에서 제일 왼쪽 부분에 해당됨.
    하지만 test_error 가 가장 낮은 람다는 0 근처임
    즉, 람다가 낮은 3번째 모델은 Over-fitting되있음.

결론 : 우리가 모델을 학습할 때 train_data에 overfitting된 모델은 test_data를 잘 예측하지 못함. 따라서 모델을 학습할 때 모델을 train_data에 덜 학습시킬 필요가 있음! -> Regulization , Earlystopping등으로 잘 조절하자!

ps. 9주차 day2 적절한 optimizer를 선택하기 위해선 데이터의 분포를 잘 확인해야함.
(예시로 클래스 불균형이 심하면 경사하강법보다 sgd가 더 잘 작동함
최소제곱법은 가우시안 분포를 가정한 알고리즘임 -> 이상치는 가우시안 분포에 거의 없음 거의 무한에 있는 값이니
적절한 가정을 통한 방법을 사용해야 원하는 결과가 나옴)