[논문리뷰] 'Compressing Neural Networks: Towards Determining the Optimal Layer-wise Decomposition' 리뷰

안녕하세요, 밍기뉴와제제입니다. 이번 달에 리뷰할 논문은 'Compressing Neural Networks: Towards Determining the Optimal Layer-wise Decomposition'입니다.

학습된 모델의 성능 하락을 최소한으로 하면서 paramter를 최대로 압축하는 model compression에 관해 공부를 하면서 여러 논문을 봤는데요, 이 논문에서 제안한 방식이 흥미로워 리뷰를 하기로 결심했습니다.

제가 이해한게 맞다면, 이 논문에서는 전체 모델의 관점(global)과 모델을 구성하는 각 layer의 관점(local)에서 compression의 hyperparameter를 결정하는 방식을 제안하고 있습니다. 상당히 흥미로웠습니다.

그럼 지금부터 논문의 리뷰를 시작해보도록 하겠습니다.

---

1. Introduction

model compression은 모델(신경망 네트워크)의 크기를 줄여 필요한 연산량과 저장 공간을 줄이는 효과를 얻는 기법을 말합니다. 흔히 알려진 Transformer, ResNet과 같은 네트워크는 가지고 있는 parameter의 개수가 많기 때문에 제한된 연산량, 저장공간을 지닌 모바일 기기 등에서 사용하려면 model compression을 해야하는 것이죠.

model compression은 앞서 말했듯 제한된 연산량 등을 지닌 모바일 기기에 모델을 사용할 수 있게 만드는데도 쓰이지만 모델 구성에 있어 새로운 insight를 주기로 합니다.

해당 논문에선 이에 대한 예시로 여러 논문을 인용했으나, 저는 다른 분야에서 이러한 insight를 발현한 예가 떠올랐습니다. 바로 슈퍼 마리오브라더스입니다.

이미지 출처

슈퍼 마리오브라더스의 용량은 40KB입니다. 당시 슈퍼 마리오브라더스를 구동하는 패미컴이 실행시킬 수 있는 프로그램의 최대 용량이 40KB였기 때문이죠. 아주 제한된 조건이었습니다.

그래서 개발진은 이러한 조건에 맞춰 게임을 만들기 위해 사용하는 색상의 개수도 제한하고 구름의 텍스처를 색깔만 바꿔서 수풀로 쓰는 등 여러 방식을 이용했습니다.

아주 제한된 조건 속에 갖가지 지혜를 발휘했고, 그 결과로 엄청난 명작이 탄생했습니다.

이야기가 좀 딴 길로 샜네요.

아무튼, model compression은 풍부한 자원 속에서 만들어지던 모델을 제한된 조건에서도 돌아갈 수 있게 만들어주며 이에 더해 모델 설계에 대한 insight도 발현할 수 있게 해주는 중요한 존재입니다.

model compression을 수행하는 기법은 quantizaiton, distillation, pruning 등 여러가지가 있습니다. 그리고 low-rank compression가 있는데요, 저자가 제안한 방식은 low-rank compression에 관한 것입니다.

low-rank compression은 '모델 속 레이어의 parameter로 구성된 tensor를 low-rank tensor로 분해(decomposition)하는 것'을 말합니다. 이 기법은 low-rank decomposition을 기반으로 제안된 방식이구요, 딥러닝 외의 다양한 분야에 사용되었다고 합니다.

머신러닝에도 사용한 예가 있습니다. 저자는 큰 tensor를 가진 하나의 레이어를 작은 tensor를 가진 여러 레이어로 나누는 방식을 언급했습니다.

low-rank compression을 딥러닝에 사용하려니...

그러나 딥러닝에 low-rank compression을 사용하려고 하자니 해결해야 하는 문제 2개가 있습니다. 저자는 'two related, yet distinct challenges'라고 말했네요.

각 문제를 말하면 이러합니다.

1. 각 layer는 효율적으로 분해되어야 한다('local step'이라 정의)
2. 최소한의 성능 손실로 최대한의 압축률을 달성하기 위해 각 layer의 압축량을 균형 있게 조정('global step'이라 정의)

여기서 local step은 많은 연구가 있었으나 global step은 최근에 들어서야 관심을 받고 연구가 시작되었습니다. 정확히는 저자가 그렇게 말했습니다.

local step과 global step을 동시에 고려하다

방금 우리는 local step과 global step에 관한 연구 방식이 각각 존재했음을 알아냈습니다. 그런데 두 가지를 모두 고려한 연구는 없었나 봅니다.

그래서 저자는 두 가지 방식을 모두 고려한 방식을 제안했으며, 그 이름을 Automatic Layer-wise Decomposition Selector (ALDS)이라 정의했습니다.

ALDS는 반복적으로 각 layer에서 계산되는 error중 최대값을 계산하면서(global step) layer 별로 최적의 [decomposition + low-rank compression] 을 구하는(local step) 방식입니다.

이렇게 보면 어떤 방식인지 잘 감이 안잡히실거 같습니다. 저도 감이 잘 안잡혔거든요. 실은 지금도 정확히 파악하진 못했습니다. 아무튼, 저자는 ALDS라는 새 방식을 제안했고 다음 표와 같이 아주 괜찮은 성능을 보여줬습니다.

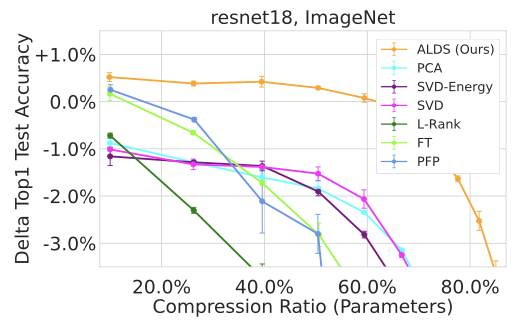
위 표는 ResNet18을 압축하면서 성능 변화를 관찰한 표인데요, ALDS가 아주 괜찮은 방식임을 확인할 수 있습니다.

그리고 저자는 ALDS가 가지는 특징 3가지를 썼는데요, 다음과 같습니다.

1. layer별로 효율적인 decomposition을 한다 : ALDS는 layer별로 SVD 기반의 decomposition을 수행합니다. ALDS는 각 layer의 tensor를 2차원 행렬로 변환 후 SVD를 적용해 2개의 행렬로 분해하고 각 행렬을 parameter로 가지는 layer를 만듭니다.
   정리하자면 (큰 layer 한 개 -> 작은 layer 두 개)인 것이죠.

2. 여러개의 subsets를 이용한 Enchanced decomposition을 수행한다 : 저자는 decomposition을 통해 생성되는 subset의 개수와 분해된 행렬들의 rank를 hyperparameter로 조정할 수 있게 설계했습니다. 그래서 각 layer에 대한 subset 개수와 rank를 조정하여 최적의 compression을 수행할 수 있게 되었죠.

3. low-rank compression을 위한 global solution을 찾을 수 있다 : ALDS는 low-rank compression을 위한 최적의 해를 hyperparameter(layer별 rank, subset개수)의 집합으로 설명할 수 있습니다. 이 때 최적의 해는 '압축된 모델의 성능 손실이 최소한인 hyperparameter의 집합'을 의미합니다. 원래 global solution을 구하는 문제는 NP-완전 문제라 아주 오랜 시간을 연산해야 최적의 해를 구할 수 있었습니다. 그런데 ALDS는 이러한 최적해를 구하는 문제를 layer별로 발생하는 error중 최대값을 최소로 하는 locally optimal solution을 구하는 문제로 변환합니다. NP-완전 문제를 효율적으로 풀 수 있게 변환해주는 것이죠. 그리고 저자들은 layer별 압축률-error의 trade-off 관계를 설명하기 위해 Eckhart-Young-Mirsky Theorem을 기반으로 하는 spectral norm bound를 유도했으며 이 bound를 이용해 효율적으로 possible per-layer decomposition하는 최적의 세팅을 구할 수 있다고 합니다.

솔직히 3번은 어...아직도 제대로 이해하지 못했습니다. 저는 그냥 '우리 방식은 global solution도 근거 있게 잘 찾을 수 있어요!'쯤으로 이해했습니다.

그리고 ALDS의 대략적인 그림을 보여주며 Introduction은 끝이 납니다. 그 대략적인 그림은 다음과 같습니다.

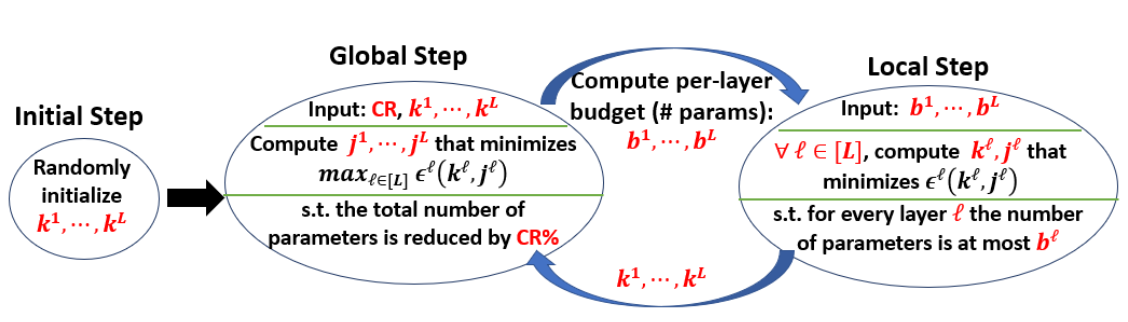
Global step과 local step을 번갈아가면서 수행하며 최적의 hyperparameter를 찾는다는 의미로 이해하시면 되지 않을까 싶습니다. 솔직히 저는 위 그림보다 나중에 등장하는 pseudo code를 보고 'ALDS가 이런 방식이구나~'라고 이해할 수 있었습니다.

2. Method

이제 ALDS에 대해 자세히 알아봅시다. 2.1장과 2.2장에서는 각각 local step과 global step에 관해 알아본 뒤 2.3장에서는 local step과 global step을 모두 이용해 model compression을 수행하는 과정을 알아보겠습니다.

2.1 Local Layer Compression

저자는 모델을 구성하는 convolutional layer(이하 conv layer)를 위한 low-rank compression 방식을 제안했습니다. 비록 conv layer를 위해 설계했으나 fully connected layer(이하 fcn), 즉 PyTorch의 Linear 레이어는 커널이 1x1이고 stride가 1인 conv layer와 같기 때문에 fcn에도 적용할 수 있습니다.

Compressing convolutions via SVD.

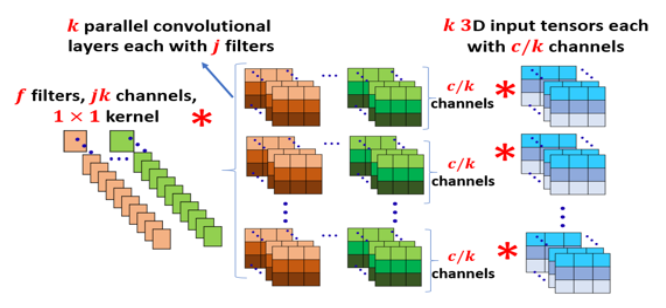
먼저 compressing을 어떻게 하는지 살펴봅시다. c채널을 가진 입력 데이터를 (k_1 x k_2) 사이즈의 커널 f개로 구성된 필터를 가진 conv layer는 weight tensor W ∈ R^(f x c x κ_1 × κ_2)를 가지고 있습니다.

텐서와 행렬이 구체적으로 어떤 차이가 있나 궁금했는데 찾아보니 '행렬은 정보를 구성하는 2차원의 테이블이며 텐서는 이를 일반화한 것이다'라고 나와있더군요. 2차원 텐서 = 행렬이라 생각하면 될 것 같습니다. 어쩌면 이게 아닐 수도...? 우선 저는 여기서 해당 정보를 얻었습니다.

아무튼, 이 4차원 행렬을 가진 conv layer를 (f x ck_1k_2)의 행렬을 가진 fcn으로 reshape을 해줍니다.

3차원 이상의 텐서는 모르겠는데, 2차원의 행렬의 경우 decomposition을 수행하는 방법은 여러가지가 있습니다.

대표적으로 지닌 정사각형 행렬을 고유값(eigen value)과 고유 벡터(eigen vector)를 이용해 간단히 분해할 수 있는 고유값 분해(Eigen Decomposition)와 정사각형이 아닌 행렬을 transpose를 이용해 decomposition을 수행하는 SVD(Singular Value Decomposition)가 있습니다.

저자는 그 중 SVD를 이용해 (f x ck_1k_2) 행렬을 (f x j), (j x ck_1k_2)로 분해했습니다. 이 때 j를 어떻게 하냐에 따라 model compression의 효과가 결정됩니다. 중요한 값이죠. 나중에 다시 말씀드리겠지만, ALDS를 수행하며 layer별로 적절한 j를 찾을 수 있습니다.

아무튼, 이렇게 해서 각각 (f x j), (j x ck_1k_2) 사이즈의 행렬을 얻었습니다. 여기서 끝나면 좋겠지만 아쉽게도 얘는 conv layer에 있던 weight를 변환한 것입니다. 이말은 즉, conv layer에서 쓸 수 있게 2차원 행렬들을 4차원의 텐서로 변환시켜줘야 한다는 뜻이죠.

다행히도, 변환은 쉽습니다. 하나씩 살펴보면 다음과 같습니다.

1. (f x j) 행렬 : (f x j x 1 x 1) 텐서로 변환시켜 (1 x 1)사이즈의 커널 f개를 가지고 j개의 채널을 지닌 입력 데이터를 처리하는 conv layer의 weight로 만들어줍니다.

2. (j x ck_1k_2) 행렬 : (j x c x κ_1 x κ_2) 텐서로 변환시켜 (k_1 x k_2)사이즈의 커널 j개를 가지고 c개의 채널을 지닌 입력 데이터를 처리하는 conv layer의 weight로 만들어줍니다.

그러니까 최종 정리를 하면

(R_f x c x κ_1 × κ_2) 텐서를 가진 conv layer => [(j x c x κ_1 x κ_2) 텐서를 가진 conv layer -> (f x j x 1 x 1) 텐서를 가진 conv layer]

로 변환되는 것이죠.

Multiple subspaces.

저자는 conv layer의 4차원 텐서를 SVD로 분해하기 전에 column들을 k >=2 개의 subspace로 나눕니다. 논문에서는 'cluster 했다'고 나와있습니다.

clustering을 수행하는 방식은 여러가지가 있습니다. 저자는 k-means 혹은 projective clustering을 고려했으나 얘들을 사용할 경우 expensive approximation algorithms을 사용해야 하는데 그러면 'optimization-based compression framework와 clustering방식을 통합하는 능력'에 제한이 생긴다고 합니다. 가슴 깊이 이해하지는 못했으나 대략적으로 'model compression의 성능에 한계가 생긴다' 쯤으로 이해했습니다.

그리고 위 방식들과 같은 arbitrary clustering은 입력 tensor의 re-shuffling을 요구할 수 있으며 그럴 경우 inference 동안 심각한 slow-down일어날 수 있다고 말합니다.

그래서, 저자는 channel slicing이라고 하는, 단순한 clustering방식을 채택했습니다. channel clustering은 단순히 c채널의 입력 데이터를 k개로 나누는 방식입니다. 그러면 이제 각 텐서는 최대 c/k 채널을 가진 텐서가 될 것입니다. 단순히 나누기 때문에 각 텐서들은 서로 연속된 값을 가질 것이구요.

짐작하셨겠지만, 이 때 k도 ALDS를 수행하는 과정에서 적절한 값을 얻을 수 있습니다.

channel slicing은 구현 방식도 쉽습니다. PyTorch의 경우 grouped convolution이란게 있어 효율적으로 구현할 수 있다고 합니다. 그리고 이를 이용할 경우, 압축된 모델의 실질적인 성능 향상도 보장해준다고 하네요. 제가 잘 이해한건지 모르겠습니다.

Overview of per-layer decomposition.

우리는 Compressing convolutions via SVD와 Multiple subspaces를 확인하였습니다. 그러니 이번에는 이 두가지 과정과 정수 j, k를 이용해 4차원 텐서를 지닌 conv layer를 압축하는데 쓰이는 전체적인 과정을 살펴보겠습니다.

1. Partition : conv layer의 4차원 텐서 W ∈ R^(f x c x κ_1 × κ_2)에 channel slicing을 적용해 k개의 W_i ∈ R^(f x c_i x κ_1 × κ_2)들로 나눠줍니다.

2. Decompose : 각 W_i ∈ R^(f x c_i x κ_1 × κ_2)를 (f x c_iκ_1κ_2)의 2차원 행렬로 변환 후 SVD를 적용해 2개 행렬로 분해합니다. 이 때 분해되는 행렬을 각 U_i ∈ R^(f x j), V_i ∈ R^(f x c_ik_1k_2)로 정의합니다.

3. Replace : U_i, V_i을 각각 4차원 텐서로 변환하고 이를 weight로 가지는 conv layer를 만듭니다. 이말은 즉, (W_i을 가진 conv layer)를 (U_i를 가진 conv layer) + (V_i를 가진 conv layer)로 대체 한다는 뜻과 같습니다.

둘로 나뉘어진 conv layer와 원래 conv layer의 차이를 그림으로 나타내면 다음과 같습니다.

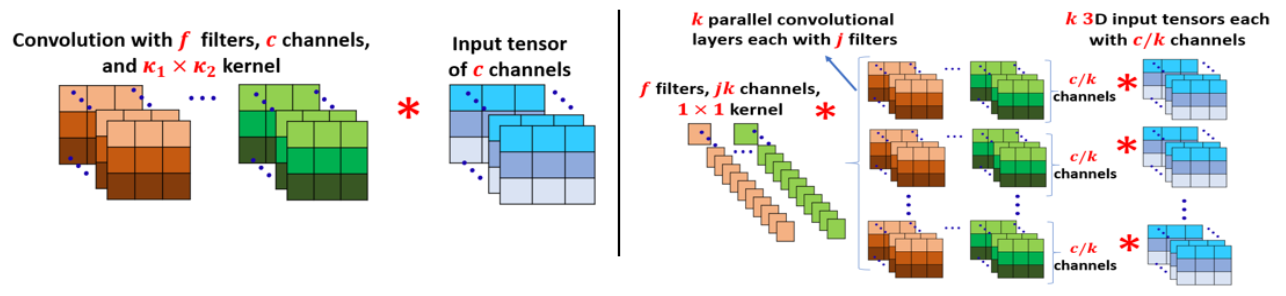
Decomposition의 효과는?!

정리해보자면 결국 텐서 하나를 여러개로 나눈다는 겁니다. 이게 도대체 뭔 효과가 있는 걸까요?

바로 parameter의 개수가 바뀝니다. 원래 conv layer가 가진 parameter는 (f x c x k_1 x k_2)개였습니다.

그런데 여러개로 decomposition을 하고 나니까 (fxj) 크기의 텐서 k개 + (jxk_1xk_2)크기의 텐서 k개 = j(fxk + cxk_1xk_2)개가 되었습니다.

곱해야할 부분이 더하기로 전환된 것이죠. 그러니 parameter의 개수가 줄어들 수 있을 것입니다. 그리고 보시면 알겠지만 j, k가 parameter의 개수에 영향을 미치는 것을 알 수 있습니다. 쟤들을 최소로 하면 parameter개수가 최소가 되겠으나 그러면 성능이 많이 떨어질 수 있습니다.

그러니 성능을 최대한 유지하면서 parameter를 최소로 하는 최적의 j, k를 찾는게 중요해집니다. 이 역시 나중에 말씀드릴 부분이긴 하나 갑자기 생각 나서 미리 적게 되었네요. 아무튼 그렇습니다.

2.2 Global Network Compression

다음으로 모델의 전체적인 압축률을 달성하면서 성능 보존을 최대한으로 하는 global step에 대해 설명드리도록 하겠습니다.

우리는 각 layer의 parameter 개수를 특정 압축률에 맞게끔 줄이면서 성능을 최대한으로 보존해야 합니다. 특정 압축률'만' 달성하는 것은 쉽습니다. 모델의 parameter를 줄이다 보면 특정 압축률에 도달할 것이기 때문이죠.

그러나 특정 압축률에 도달할 수 있는 경우의 수는 다양합니다. 예를 들어 parameter가 100개인 layer 2개로 구성된 모델을 50% 압축을 할 때 첫 번째 layer를 20개, 두 번째 layer를 80개로 압축해도 50% 압축이고 첫 번째 layer를 90개, 두 번째 layer를 10개로 압축해도 50% 압축이 됩니다.

layer별로 얼마나 압축하냐에 따라 결정되는 성능은 매우 다양합니다. 그렇기 때문에 '최대 성능을 가질 수 있게끔 특정 layer의 parameter를 특정 비율만큼 줄이기'에 대한 최적의 해를 찾는게 정말 중요합니다. 잘못 압축하면 성능이 바닥을 길 수도 있으니까요.

그러나 해당 최적해를 찾는 문제는 경우의 수가 매우 다양합니다. parameter의 개수가 늘어날 수록 그 수가 더 늘어나겠죠? 저자는 '이 문제는 NP-완전 문제다' 라고 했습니다. 쉽게 말해 시간이 매우 오래 걸릴 문제라 말한 것이죠. 한 세월 걸릴겁니다.

그렇다고 포기해야 하는가? 그럴 수는 없습니다. 최적의 해를 못찾으면 근사해라도 찾아야죠.

근사해를 찾는 방식은 이전 연구들에서도 제안된 적이 있습니다. 대표적으로 한가지 꼽자면 '모든 layer에 똑같은 압축률을 적용하는 것'이죠. 제일 간단한 방식입니다. 그러나 이 방식을 수행할 경우 최선의 해와 아주 근사한 해를 찾기는 힘들 것입니다.

그래서, 저자는 the maximum relative error incurred across layers를 줄이는 것을 목표로 하는 efficiently solvable global compression framework를 제안하였습니다. 목표를 변경함으로써 얻는 이득이 무엇일까요?

그럼 지금부터 global compression framework에 대해 자세히 알아보도록 하겠습니다.

The layer-wise relative error as proxy for the overall loss.

overall loss는 모델을 압축한 뒤 추가적으로 발생하는 loss를 말합니다. 성능이 떨어진 정도를 나타내는 것이죠. 저자는 이 추가적인 loss를 줄이는 문제는 NP-완전 문제라고 말했습니다. 최적해를 찾기 글렀다는 뜻이죠.

그래서 저자는 overall loss 대신 maximum relative error를 줄이는 문제를 해결하기로 했습니다. 해결할 대상을 바꾼 것이죠.

maximum relative error는 layer별 theoretical maximum relative error 중 최대값을 의미합니다. 식으로 나타내면

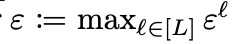
이와 같습니다. 여기서 ε^l은 l번 째 layer에서 발생하는 theoretical maximum relative error를 나타냅니다. 이에 대한 자세한 정의는 추후 설명드리도록 하겠습니다.

maximum relative error를 줄이는 것으로 목표로 한 이유?

앞서 저는 '왜 목표를 변경한 것일까?' 의문형으로 문장을 썼습니다. 문제를 바꿔서 얻을 수 있는 이득이 무엇이 있을까요?

저자는 maximum relative error를 줄이는 것을 선택한 이유로 3가지가 있다고 말했는데요, 다음과 같았습니다.

1. maximum relative error를 줄이는 것은 각 layer에서 비정상적으로 거대한 error(다른 layer로 전달되거나 증폭될 수 있는)가 발생하지 않는 것을 보장할 수 있음.
2. layer 별 scaling은 임의적으로 바뀌기(예 : batch normalization) 때문에 absolute error보다 relative error가 더 선호됨. 그리고 layer의 absolute scale은 loss의 증가를 나타내지 못할 것임.(이게 어떤 뜻일까요...)
3. layer 별 relative error는 본질적(intrinsically)으로 theoretical compression error와 연결되어 있음. Arora et al.과 Baykal et al.에서 찾아볼 수 있음.

저도 완전히 납득하진 못했습니다. 특히 3을 제대로 이해하지 못했는데요, 아마 참고문헌으로 달아둔 논문들을 읽어보면 그나마 더 이해할 수 있지 않을까 싶습니다.

Definition of per-layer relative error

앞서 말한 relative error라는게 뭔지 알아봅시다. 앞서 말할 때는 theoretical이란 말이 있었는데 여기에는 해당 단어가 빠졌네요.

l번 째 layer의 relative error는 l번 째 layer의 weight를 행렬로 변환한 W_l ∈ R^(f_l x c_lk_l1k_l2)과 이를 2.1장의 decompose 과정을 거쳐 압축된 가중치들로 재구성한 weight W_hat_l = [U_l1V_l1···U_lk V_lk]의 차이를 다음과 같이 연산한 값입니다.

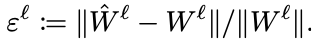
원래 압축된 모델의 layer들은 decompose된 채로 있으나 error 계산을 위해 재결합했다고 합니다.

저자는 error를 계산할 때 norm 연산을 사용했는데요, 이를 사용하면 모든 output channel에서 pixel 단위의 maximum relative error를 나타낼 수 있기 때문이라고 합니다. norm 연산이 값의 크기 등을 나타낼 때 사용하는 연산이니 납득할 수 있는 선택이라 할 수 있겠습니다.

Derivation of relative error bounds

저자는 compression에 사용하는 hyperparameter인 j_l(decompose할 때 사용하는 값), k_l(channel slicing할 때 쓰는 값)에 대한 per-layer relative error를 묘사하기 위한 error bound를 구했습니다. 논문에서는 derive했다고 적혀있습니다.

해당 error bound에 대한 정리는 다음과 같습니다.

뭔 소리야...싶을 수도 있습니다. 저도 그랬구요. 왜 이런 bound가 나온 것일까? 싶더라구요. 이에 대한 증명은 다음과 같습니다. 글로 풀어 쓰자니 너무 길거 같아 논문의 정리 부분을 캡처했습니다.

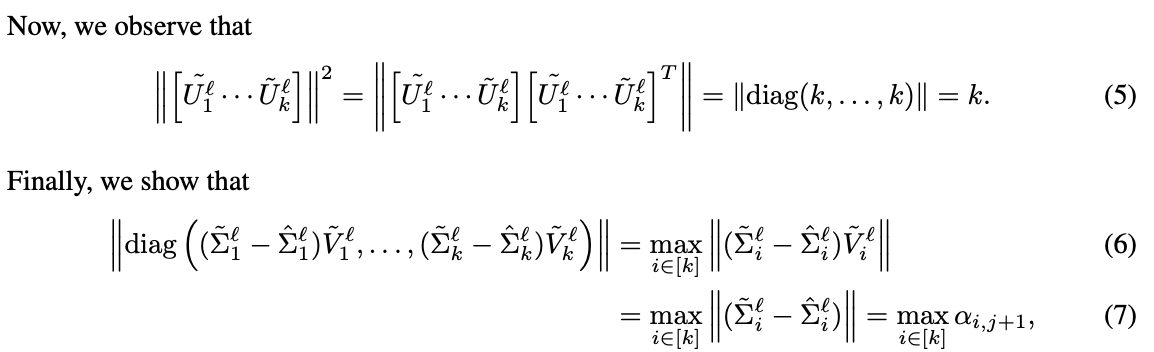
정리하자면, W_l, W_hat_l 모두 SVD를 이용해 decompose할 수 있다는 점을 가지고 뺄셈을 연산합니다.

뺄셈은 행렬의 원소 단위(element-wise)로 수행하며 앞서 우리는 decomposition 단계에서 W를 column 단위로 나누는 과정(clustering)을 했기 때문에 W_ㅣ - W_hat_l을 column 단위 연산으로 나타냈습니다.

그리고 SVD에서 시그마(Σ)는 행렬이 가진 특이값(Singular Value)들로 구성된 diagonal matrix입니다.

여기가 중요합니다. W_hat_l은 W_l의 근사값입니다. 그렇다는 말은 두 행렬의 크기가 같다는 것이죠. 그렇기에 W_hat_l을 SVD로 분해했을 때 W_l의 U, V^T(transpose 붙이는거 중요합니다!)를 가지고 있고 Σ만 다르다고 정의할 수 있습니다. U, V만 고정하고 Σ는 변수로 두는 방정식을 세우면 어떻게든 적절한 Σ가 나오기 때문이죠.

아무튼, 그러한 이유로 (3)과 같이 weight간의 뺄셈을 정리할 수 있습니다. 그리고 axb의 절대값은 a의 절대값과 b의 절대값의 곱과 같거나 작다는 성질을 이용해 (4)의 식을 만듭니다.

그리고 식 (5)가 있는데요, 어...왜 저게 유도되는지 잘 모르겠습니다. 그러니까 SVD를 수행할 때 U, V는 모두 normalized된 행렬들입니다. 즉, 크기가 1인 것이죠.

그렇기에 U들은 모두 크기가 1인 행렬들일텐데 걔들이 k개 모였고 이걸 식 (5)와 같이 AA^T의 연산을 한게 왜 diag(k...k)가 나오는지 이해가 안되네요.

그리고 최종적으로 식 (6) ~ (7)이 나오는데 여기도 이해를 잘 못했습니다. 아...어렵네요.

여튼 우리는 식 (5)와 (7)을 얻었습니다. 얘들을 식 (5)의 오른쪽에 대입하면

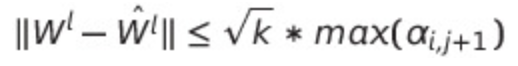
이렇게 나옵니다. 그리고 이 식의 양쪽 항에 ||W_l||을 나눠주면 됩니다. 그런데 논문에는 a_1이라 적혀있습니다.

왜냐하면 W_l의 norm은 W_l의 singular value 중 제일 큰 값인 a_1과 같기 때문입니다. SVD의 주요 특성 중 하나입니다.

힘든 증명이었습니다. 중간에 모르는 것도 있어서 스킵한게 있었으나 그래도 어찌저찌 여기까지 왔네요. 이로써 우리는 relative error은 상한선이 있으며 그 값은 hyperparameter인 j, k에 의해 결정된다는 것을 알아냈습니다.

Resulting network size

앞서 우리는 layer의 parameter는 (f x c x k_1 x k_2)개 있으며 압축된 layer는 j(fxk + cxk_1xk_2)개의 parameter를 가지고 있음을 확인했습니다.

그러니 L개의 layer를 가지는 모델의 경우, l번 째 layer가 가지는 parameter의 개수는

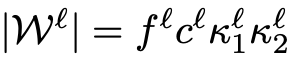
위와 같고 모델이 가지는 parameter와 그 개수를


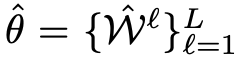
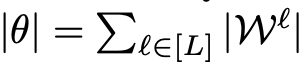
위와 같이 나타낼 수 있습니다. 압축된 모델은 다음과 같이 나타낼 수 있겠습니다.

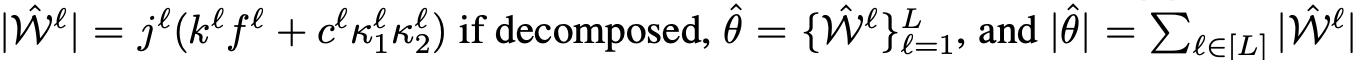
그렇기에 우리는 전체적인 압축률을 다음과 같이 나타낼 수 있습니다.

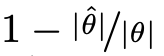
여기서 |W_l|은 hyperparameter k_l, j_l에 의해 결정되는 값임을 다시 한 번 기억하고 넘어가봅시다.

Global Network Compression

최종 정리 단계입니다. 우리는 layer별로 relative error, 다시 한 번 줄여서 말하면 ε을 구했고 이 과정에서 j, k의 중요성을 깨달을 수 있었습니다.

이러한 점을 모두 모아, 저자는 layer별로 최적의 j, k를 결정할 수 있는 ε_opt를 다음과 같이 정의하였습니다.

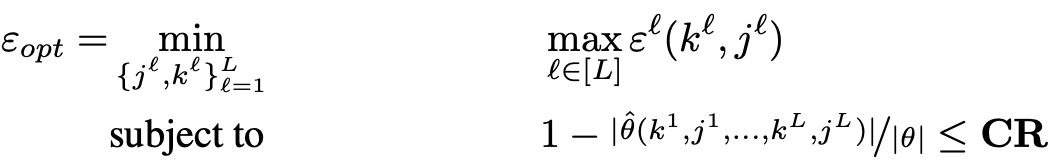
그러니까 우리는 적절한 압축률을 준수하며 ε_opt를 달성할 수 있는 j, k의 집합을 구해야 하는 것이죠. 어렵습니다.

2.3 Automatic Layer-wise Decomposition Selector (ALDS)

그러면 최적의 j, k는 어떻게 구하는 것이죠? 저자는 최적의 maximum relative error를 구하는 방법으로 'error가 수렴할 때 까지 계속해서 j, k의 조합을 찾아보자'는 전략을 제안했습니다. 명확합니다.

저자는 이 과정을 pseudo code로 작성해줬는데요, 다음과 같습니다. 이해하기 쉽게 작성되어 있으며 저도 이 코드를 보고 제안된 method에 대한 이해도를 높일 수 있었습니다.

error가 수렴할 때까지 최적의 j, k 집합을 찾는 과정을 n번 수행합니다. 그러면 n개의 j, k 집합을 얻을 수 있을 것이며 그 중 error가 가장 낮을 때의 j, k 집합이 최종해가 되는 것이죠.

그리고 4번 째 줄의 'j_1,...,j_L ← OPTIMALRANKS(CR,k1,...,kL)'는 한 줄로 구성되었으나 [j_1,...,j_L 찾기 -> 압축된 모델의 크기 구하기]를 주어진 CR을 만족할 때까지 반복 수행합니다.

그리고 4, 7번 째 줄은 Rank j와 subspace의 개수 k를 구하는 부분인데 이 때 SVD를 사용합니다. 해당 과정의 연산적 복잡성은 앞서 error bound에 관한 정리를 이용해 줄일 수 있다고 하는데 음...잘 모르겠습니다.

보다 자세한 내용은 supplementary에 나온다고 하니 관심 있으면 살펴보시면 됩니다.

Extensions.

ALDS는 layer별 compression를 하는 과정에서 SVD를 사용했습니다. 그런데 ALDS는 다른 low-rank compression 기법과 쉽게 합체할 수 있다고 합니다. 특히, subspace 개수를 구하는 과정에서 SVD 외의 또다른 decomposition 기법을 사용할 수 있다고 하네요.

이에 더해 relative error를 구할 때도 보다 효율적인 방식을 사용할 수 있을 것이라고도 말했습니다. 보다 자세한 내용은 supplementary에 나오니 궁금하면 확인하시면 되겠습니다.

3. Experiments

드디어 Experiment입니다.

저자는 다양한 실험을 수행했으나 결과적으로 말하는 것은 '우리가 제안한 방식으로 모델 압축하니까 압축률 대비 성능 보존이 제일 좋았다!'는 것이었습니다. 그래서 간단히 살펴보고자 합니다.

실험을 위한 학습 -> 압축

저자는 압축 방식들을 평가하기 위해 다음과 같은 과정을 수행했습니다.

1. Train : 압축 전 모델들을 우리가 아는 방식(e 에포크만큼 learning schedule 따라 학습시키기)으로 학습시킵니다.
2. Compress : 각 압축 방식대로 모델들을 압축합니다.
3. Retrain : 압축한 모델을 재학습 시킵니다. 이 때 epoch는 r이며 hyperparameter는 과정 1에서 [e-r, e] 구간에 설정한 값을 사용합니다. (즉, e >= r입니다.)
4. (선택 사항) 압축한 애들을 압축 전 사이즈로 reconstruct한 뒤 1-3의 과정을 다시 수행합니다.

평가 지표

저자는 Top-1, Top-5, IoU를 test accuracy로 사용하고 CR-P, CR-F를 압축률에 관한 지표로 사용했습니다. 각 실험은 3번씩 반복되었고 실험 별로 나온 값들을 이용해 평균과 분산을 구했다고 합니다.

3.1 One-shot Compression on CIFAR10, ImageNet, and VOC with Baselines

실험 수행에 관한 정보들을 알아봤으니 결과를 알아볼 시간입니다. 맨 처음 실험은 CIFAR10, ImageNet, VOC로 학습시키고 e=r로 설정하였습니다.

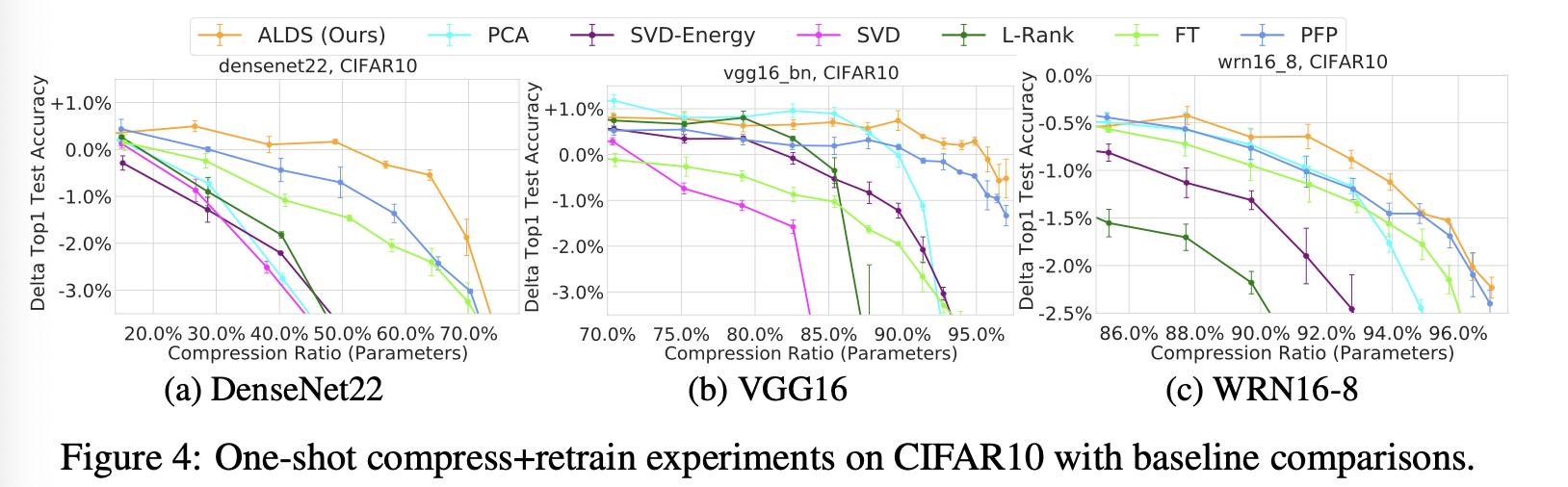
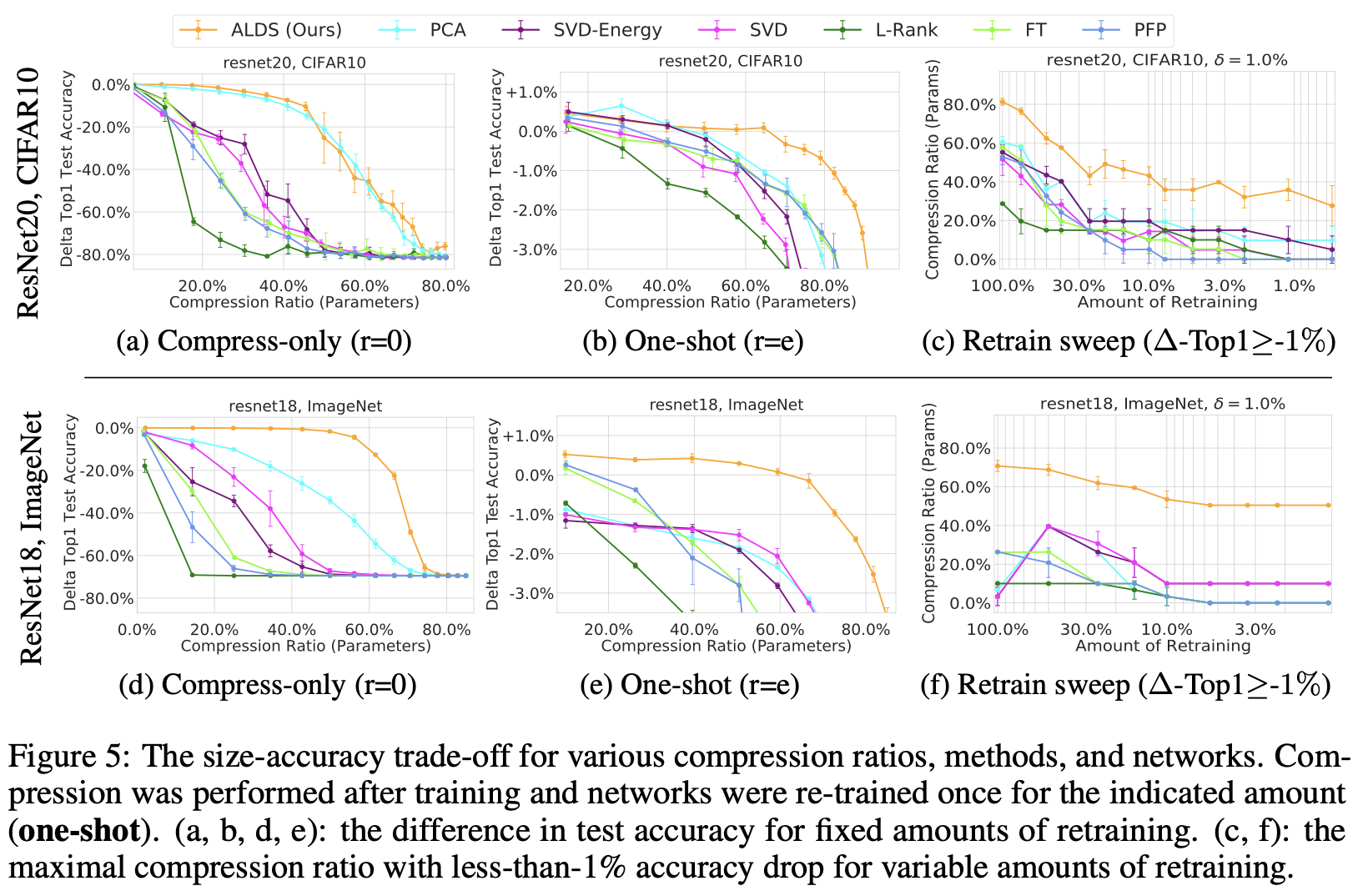
이번 실험의 결과를 정리하면 위와 같습니다. 모든 경우에서 ALDS가 제일 괜찮았던 것을 알 수 있습니다.

저자는 figure에 더해 table까지 제작하였습니다.

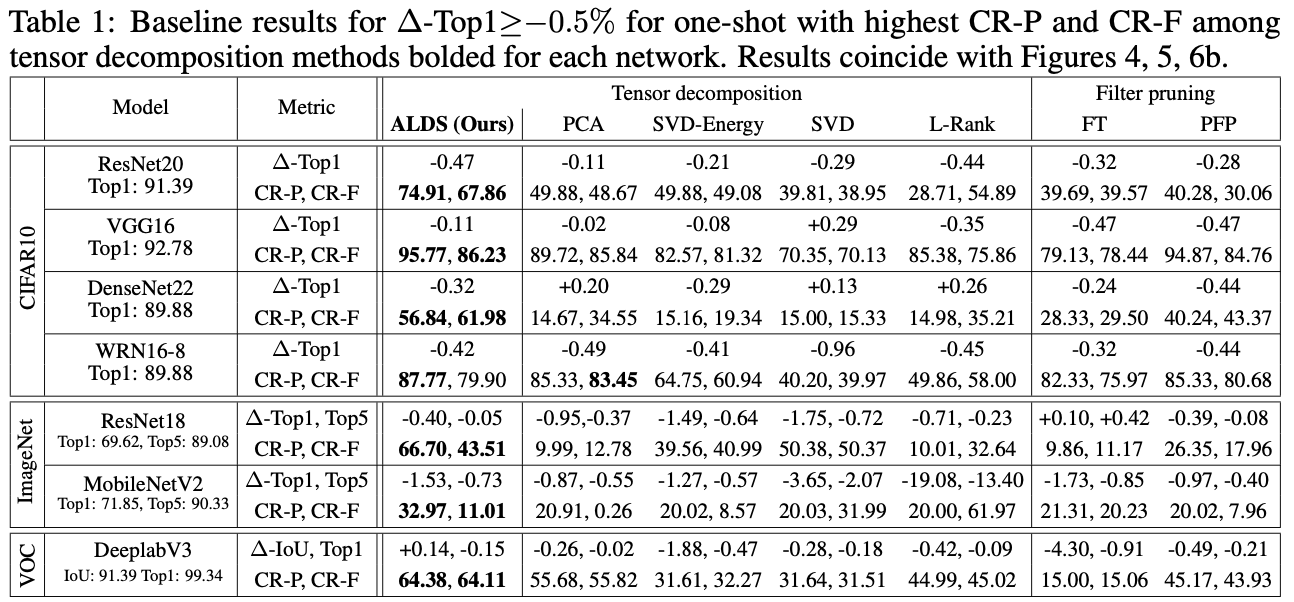
어떠한 model, dataset에서도 우수한 성능을 보여주는 것을 확인할 수 있습니다.

3.2 ImageNet Benchmarks

저자는 ImageNet을 사용해서도 실험을 수행했습니다. ResNet18과 AlexNet을 이용해 실험을 수행하였고 그 결과는 다음과 같습니다.

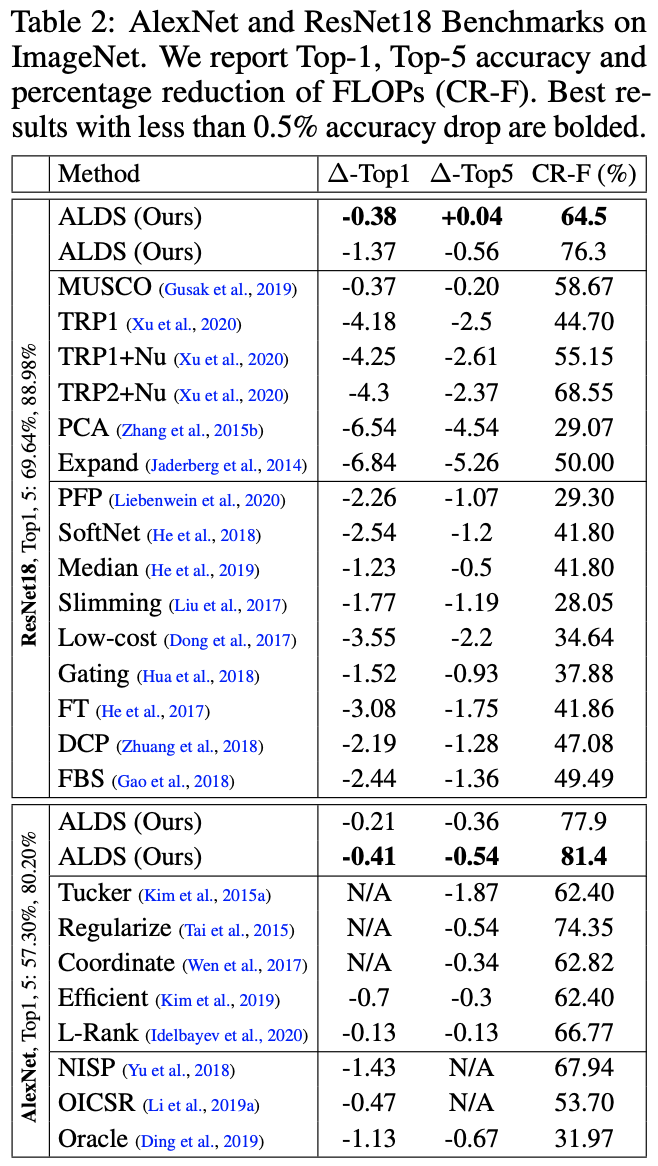
3.3 Ablation Study

이 실험에서는 ALDS의 주요 요소인 'layer별 압축률 설정'과 'layer별 subspace 개수 설정'의 중요성을 다시 한 번 확인였고 이에 더불어 weight를 나눴던 방식인 channel slicing 대신 다른 방식을 사용하여 channel slicing의 중요성도 확인하는 시간을 가졌습니다.

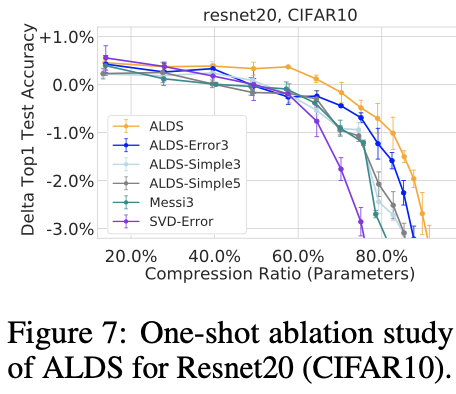
실험 결과를 통해 저자가 제안한 local step, global step을 위해 제안된 방식들이 중요함을 깨달을 수 있습니다.

4. Related Work

model compression을 주제로 해서 그런지 prunung, compression의 내용이 나옵니다.

제가 model compression에 대해 잘 모르고 있어서 그런지 Related work가 많은 도움이 되었습니다. 저와 같이 해당 주제가 생소하신 분들은 읽어보시는 것을 권장드립니다.

5. Discussion and Conclusion

여기서는 본인들이 제안한 ALDS의 강점을 정리한 뒤 이를 어떤 방식으로 발전하면 좋을지 제안하는 내용이 들어있습니다. 논문에 나왔던 내용을 다시 적는 느낌이 들어서 스킵하도록 하겠습니다.

---

리뷰 후기

리뷰는 아주 힘들었으나 많은 공부를 할 수 있는 논문이었습니다. 많이 접하지 않은 분야라 이해도가 매우 낮은데도 불구하고 비교적 무난하게 읽을 수 있었습니다.

제가 이 논문을 선택한 이유는 진학하기로 한 연구실의 연구 주제가 model compression 등 Efficient Learning을 주제로 하는 곳이기 때문입니다.

연구실에서 어떤 연구를 하면 좋을지 조사를 하다가 model compression이 유용하게 쓰일거 같고 흥미로운 주제여서 하나둘씩 읽다가 이 논문이 특히 끌려서 자세히 읽고 리뷰까지 하게 되었네요.

논문을 읽으며 많은 부족함을 느낄 수 있었습니다. 특히 수학적으로 증명하는 부분에서 아직 많은 공부가 필요한 사실을 알 수 있었네요. 연구실에 들어가기 전에 수학 공부를 좀 해야될 것 같습니다.

그럼 다음 논문 리뷰 시간에 뵙겠습니다.